3.2.2Машины Тьюринга

Согласно тезису Черча любые две формальные схемы, описывающие понятие алгоритма должны быть эквивалентны друг другу.

Здесь мы рассмотрим еще одну, пожалую самую популярную из таких схем - машину Тьюринга. Подобно предыдущему формализму она предназначается для преобразования некоторого одного слова P в заданном алфавите в другое слово Q.

Заметим, что существует несколько разновидностей МТ. Более того, даже для одного и того же типа МТ определения могут варьироваться. Это может быть связано с мелкими техническими удобствами, а также с попытками не загромождать формализма "очевидными" тонкостями.

Рассмотрим самый простой объекта - одноленточную детерминированную МТ. Она представляет собой пятерку {S, A, F, q₀, }, где S={q₁,…q_k} - конечное множество, элементы которого называются состояниями, A={a₁,…,a_n} - алфавит, FS. Элементы F называются конечными состояниями, выделено начальное состояние q₀ и схема переходов машины Тьюринга . Каждый такой переход еще называется командой, а вся схема (список команд) представляет собой частично определенное отображение из SASA{L, R, St}. Здесь {L, R, St } - множество из трех элементов, смысл которых ниже поясняется.

Опишем теперь механизм работы МТ. На двусторонней бесконечной ленте, разбитой на ячейке, начиная с некоторой ячейки, записано входное слово P (по одному символу в каждой ячейке). Имеется еще один объект - "головка" МТ, который характеризуется наличием определенного приписанного ей состояния и умением читать и писать.

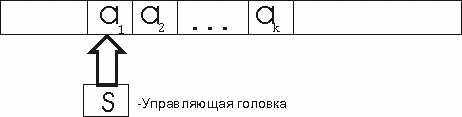
Работа МТ состоит из последовательности тактов.

В начальный момент времени головка обозревает ячейку ленты, в которой записан первый символ входного слова, и находится в начальном состоянии.

Вообще, положение головки, ее состояние и запись на ленте полностью описывают конфигурацию МТ в данный момент времени. Поэтому конфигурацией МТ и называется слово v₁…v_kq_jv_k+1…v_m. Эта запись свидетельствует о том, что в данный момент времени головка МТ находится в состоянии q_j и обозревает ячейку ленты, в которой записан символ v_k+1. Все же слово, записанное к этому моменту на ленте, имеет вид v₁…v_kv_k+1…v_m.

Каждой конфигурации K=v₁…v_kq_jv_k+1…v_m однозначно сопоставляется пара конфигурации q_jv_k+1и слово конфигурации v₁…v_kv_k+1…v_m.

Такт работы представляет собой переход из одной конфигурации к другой. Этот переход осуществляется путем выполнения некоторой команды q_ia_j q_ra_t{Z}. (Пару q_ia_j назовем левой частью команды q_ia_jq_ra_t{Z}, а тройку q_ra_t{Z} - правой частью этой команды.) Если пара конфигурации не является левой частью ни одной из команд, то МТ останавливается и процесс ее работы заканчивается.

Если же такая команда q_ia_j q_ra_t{Z} найдена, то это означает, что перед выполнением данного такта МТ находилась в состоянии q_i, обозревала ячейку с символом a_j, а после выполнения данного такта она перешла в состояние q_r, в ранее обозреваемой ячейке появился символ a_t .Z имеет одно из трех значений L, R, St. В первом случае головка сдвинулась на данном такте на одну ячейку влево, во втором - вправо, в третьем - осталась на месте. Если q_r является конечным состоянием, то процесс работы МТ заканчивается и МТ останавливается. В противном случае для вновь полученной конфигурации ищется команда, правая часть которой совпадает с парой конфигурации, и процесс продолжается.

Так как каждая команда определяется однозначно, то, в отличие от НАМ, порядок команд в списке не имеет значения.

Переход от конфигурации K_i к конфигурации K_j в результате выполнения некоторого такта работы МТ обозначим через K_iK_j. Если существует такая последовательность команд, что в результате их выполнения МТ перешла из конфигурации K_i к конфигурации K_j, то эту ситуацию обозначим через K_iK_j.

Заметим, что МТ может зацикливаться. Это довольно тонкий момент в данном формализме, который восходит к тому факту в определении алгоритма, согласно которому алгоритм не обязан сам распознавать слова из своей области действия. Конечно, если мы требуем, чтобы перед началом работы была проведена проверка на соответствие входного слова области действия, то никакого зацикливания не может быть, так как уже на стадии проверки будут отсеяны те слова, на которых алгоритм не может корректно работать (слова, которым он не применим). Если же такой предварительной стадии нет, то она может быть заменена предположением о том, что у нас есть некоторый механизм идентификации зацикливаний. То есть, мы можем различать три ситуации: МТ остановилась и завершила свою работу; МТ находится в процессе работы, совершив некоторой количество переходов, и готовится к очередному такту работы; МТ зациклилась, т.е. будет работать и никогда не остановится.

Если МТ на входном слове P за конечное число тактов останавливается, то говорят, что она применима к этому слову. Последовательность конфигураций от начальной до конечной называется вычислением МТ на слове P.

В отличие от НАМ в данном формализме присутствуют такие понятия как: читающая и пишущая головка, обозреваемая ячейка, сдвиги вправо и влево и пр. Все это с точки зрения формальной схемы интуитивного понятия "алгоритм" также нуждается в формализации. Она более или менее очевидна, особенно с точки зрения людей, знакомых с азами компьютерной техники. (Заметим, что Тьюринг предложил свой формализм в 1935 году, когда о компьютерах еще и речи не было). Предположим, что все эти детали определены, и мы получили некоторый алгоритм _T,C. Он работает в алфавите C, C является надалфавитом алфавита A машины Тьюринга Т. А для любых слов P и Q в алфавите С соотношение _T,C(P)=Q выполняется тогда и только тогда, когда существует такое вычисление на машине Тьюринга Т такое, что оно начинается с конфигурации q₀R и заканчивается конфигурацией R₁q_iR₂, где R₁R₂=Q.

Вообще же произвольный алгоритм  в алфавите D называется вычислимым по Тьюрингу тогда и только тогда, когда существует машины Тьюринга T с алфавитом A и алфавит C, являющийся надалфавитом AD такие, что алгоритмы _T,C и  вполне эквивалентны относительно D.

Перейдем теперь к рассмотрению примеров.

Пример 1. Построить МТ, вычисляющую функцию T(X)= (машина стирает любой слово).

Входной алфавит: A={a₁…a_n}.

Множество состояний состоит из единственного начального состояния q=q_0.

Работа МТ описывается единственной командой: .

Пример 2. Построить МТ, вычисляющую функцию T(x,y)=x+y.

Алфавит A=(*,1).

При этом сохраняем договоренность о том, что через обозначаются любые символы алфавита.

На входе мы имеем 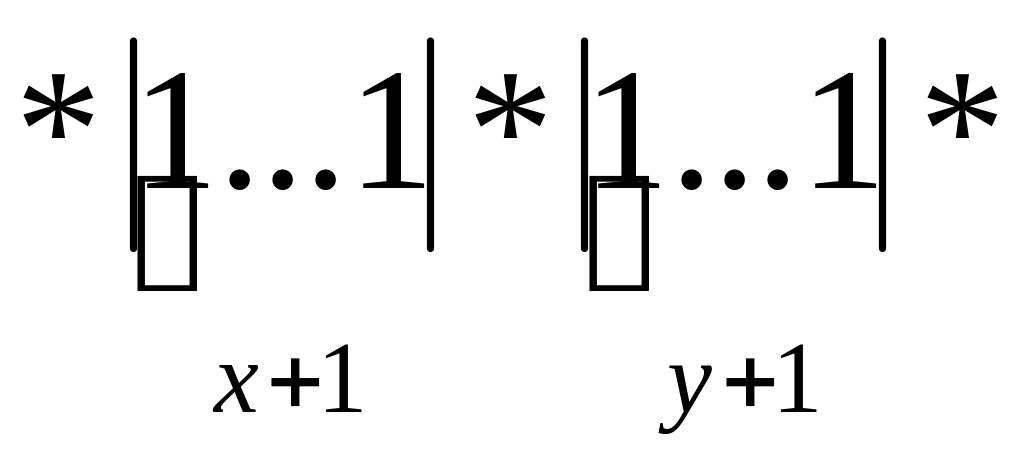. На выходе - * .

Теорема: Пусть M – машина Тьюринга, вычисляющая функцию f, тогда существует нормальный алгоритм Маркова, вычисляющий ту же функцию.

Доказательство: A – алфавит МТ, S – множество отношений, B = A S.

a,b A, q, q’ S

Машина Тьюринга	Нормальный Алгоритм Маркова
δ(q,a) = (q’, b, S)	qa→q’b
δ(q,a) = (q’, b, R)	ck: qa ck → bq’ ck qa → bq’_’
δ(q,a) = (q’, b, L)	ck: ck qa → q’ckb

q_i → ∙λ , q_i F

λ → q₀

Сложность (количество действий):

С_нам(n)≤С_мт(n)+2

С_нам(n) =O(С_мт(n))

Существует и обратная теорема: Если существует НАМ, вычисляющий функцию f, тогда существует и МТ, вычисляющая ту же функцию.

Тезич Чёрча: Любой алгоритм можно реализовать на МТ (и на НАМ).

f: A^*→{0, 1} – функция распознавания, она может быть вычислена с помощью машины Тьюринга, она задает язык для алфавита A.

Вопрос: Любая ли такая функция может быть вычислимой?