10.6Спектр кода. Эквидистантные коды

Рассмотрим код V = (v₁…v_k). Тогда для кодового слова v_i r_s(v_i) – число кодовых слов, т.ч. ρ(v_j, v_i) = s. v_i сопоставляется (r₀(v_i)…r_k(v_i)) – спектр v_i – кода.

Если V – линейный, то спектры всех v_i одинаковые. Поэтому для линейного кода спектром называется вектор (a₀…a_n), т.е. число кодовых слов весов 0…n.

Теорема Маквильямса:

Пусть есть код V и его спектр (a₀…a_n) и код ортогональный V* и его спектр (b₀…b_n), тогда проведем соотношения , где z – переменная.

Это выражение дает возможность сразу выражать спектр кода через спектр ортогонального кода.

Следствие:

Пусть

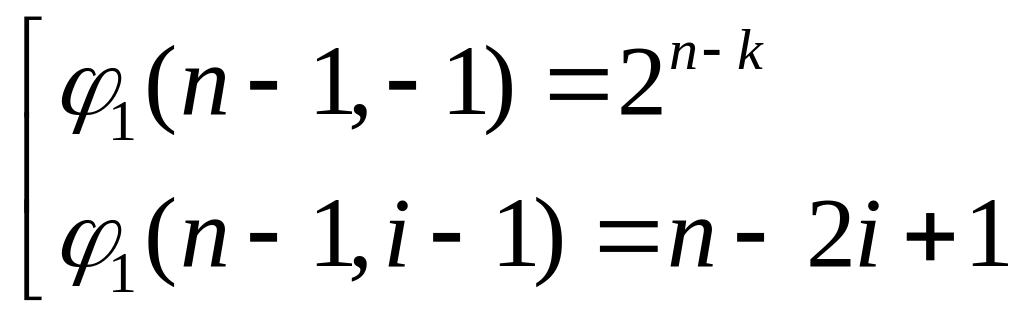
Следствие 1:

Следствие 2:

, где - число точек B_n веса S на расстоянии r от некоторой точки кода.

Тогда C(S) – число точек Bⁿ веса S, попавших в шар радиуса T линейного кода, исправляющего t ошибок.

Следствие 3:

Пример применения: Код Хемминга

Это совершенный код, для которого C(S) = C^S_n.

Применяем следствие 3:

Отделим из первой суммы первые слагаемые (i = 0):

Т.к. многочлен = 0 → все его коэффициенты = 0 → b₁ = b₂ = … = b_{(n – 1) / 2} = b_{(n – 3) / 2} = … = b_n = 0

n – 2i + 1 = 0

i = (n + 1) / 2

Т.е. b_{(n – 1) / 2} не равно 0, а значит спектр кода V* (0, 0…0, (n + 1) / 2, 0…0)

Опр.: Код называется эквизиститантным, если для любых i, j (i не равно j) ρ(v_j, v_i) = d.

Код, двойственный коду Хемминга называется эквизистантным (кодом

Макдональда).

n = 2^m – 1, k = m

Тогда все ρ(…) = 2^{m – 1} (число точек в коде Макдональда 2^m)

Теорема Джоши:

A(n, d) ≤ 2d / (2d – n)

Для кода Макдональда: 2d / (2d – n) = 2*2^m-1 / 2*2^m-1 – (2^m – 1) = 2^m

Т.е. любой код не может содержать более чем 2^m точек. Код Макдональда оптимален, лучше ничего не построить.

Теорема: Пусть V – эквизистантный линейный код в Bⁿ, тогда |V| ≤ n + 1

V = (v¹…v^s), ρ(v_j, v_i) = d, i не равно j.

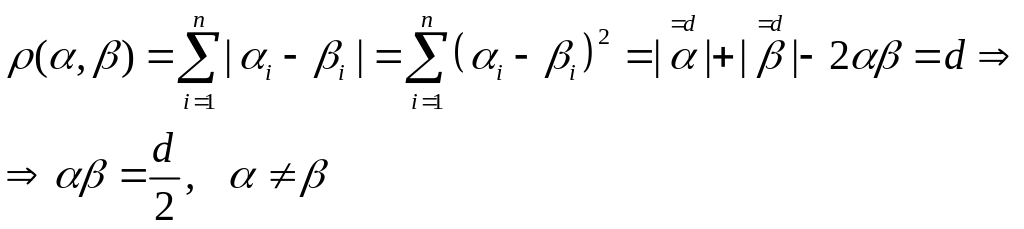
Будем считать, что 0 V

Определитель Грамма для векторов :

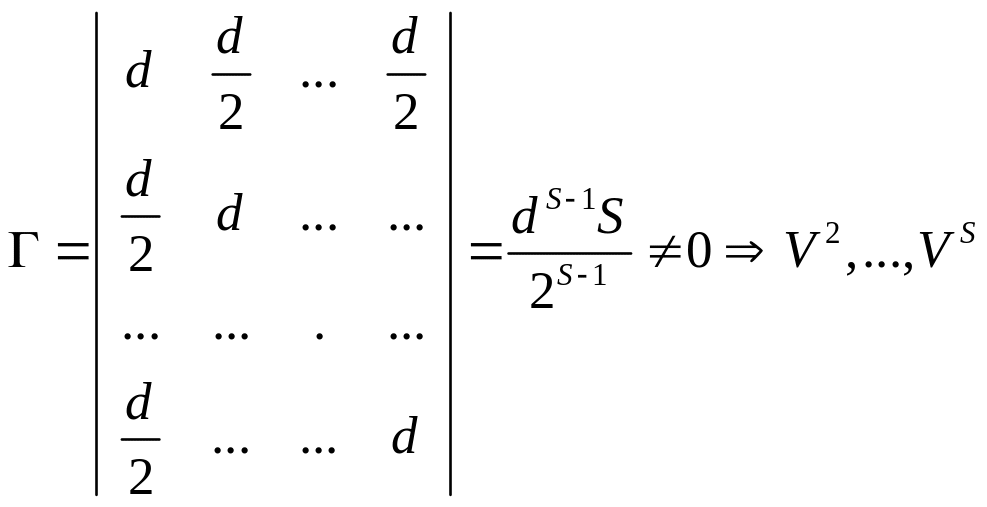- линейно независимы.

Итак, имеем S-1 линейно независимых векторов.

В пространстве Bⁿ может быть не более n линейно независимых векторов

S n+1.

11Рекомендованная литература

1. Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычислительных алгоритмов. М.: Мир, 1979.

2. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. М.: Мир, 1982.

3. Мендельсон Э. Введение в математическую логику. М.: Наука, 1971.

4. Пападимитриу Х., Стайглиц К. Комбинаторная оптимизация. Алгоритмы и сложность. М.: Мир, 1984.

5. Лидовский В.В. Теория информации: Уч. пособие. - М.: Компания Спутник+, 2004.

6. Потапов В.Н. Теория информации. Кодирование вероятностных источников.- Уч. пособие / Новосибирский государственный университет. -- Новосибирск, 1999.

7. Панин В.В. Основы теории информации: учебное пособие для вузов. - 3-е изд. испр. - М.: БИНОМ. Лаборатория знаний, 2009.

8. Кузьмин И.В. Основы теории информации и кодирования.- Электронный учебник. www.info.oglib.ru/bgl/4607.html.

9. У. Питерсон, Э. Уэлдон. Коды, исправляющие ошибки. – Мир, 1976.

79