10.3Корректирующие способности кодов. Границы мощности.

Пусть k – число информационных символов. Закодировали 2^k слов.

C(p) = 1 – H(p) – доля канала, предназначенного для информации.

Ниже (теорема Шеннона для канала с шумом) будет показано, что существуют коды, когда для любого Ԑ V(C) и 1- H(p) отличаются на Ԑ.

Опр. Код называется кодом, исправляющим t ошибок, если алгоритм декодирования

правильно декодирует все слова, в которых при передаче по каналу произошло

не более t ошибок.

Утверждение. (n,M,d)-код – код с исправлением ошибок.

Есть еще коды, обнаруживающие ошибки.

Опр. Код называется кодом, обнаруживающим t ошибок, если в случае, когда

произошло не более t ошибок, декодер выдает сообщение об ошибке.

Утверждение. (n,M,d)-код обнаруживает ошибку.

Мажоритарное кодирование – схема, где слово повторяется p раз.

a = 11 → 11|10|11|00|11|11|11 – передали по каналу 7 раз.

На первой позиции 6 раз «1» и 1 раз «0» a = 1х.

На второй позиции 5 раз «1» и 2 раза «0» a = 11.

Избыточность огромна. Уместно при высоких p (~1/10), при p~1/1000 уже бессмысленно.

Введем A(n,d) – максимальная мощность кода в Bⁿ с расстоянием d.

Утверждение. Пусть есть множество V=(α₁… α_k), . Также есть множество V’=(β₁… β_S), и для любых x,y V’: множества не пересекаются.

Доказательство. От противного.

где , .

Теорема (граница Хемминга)

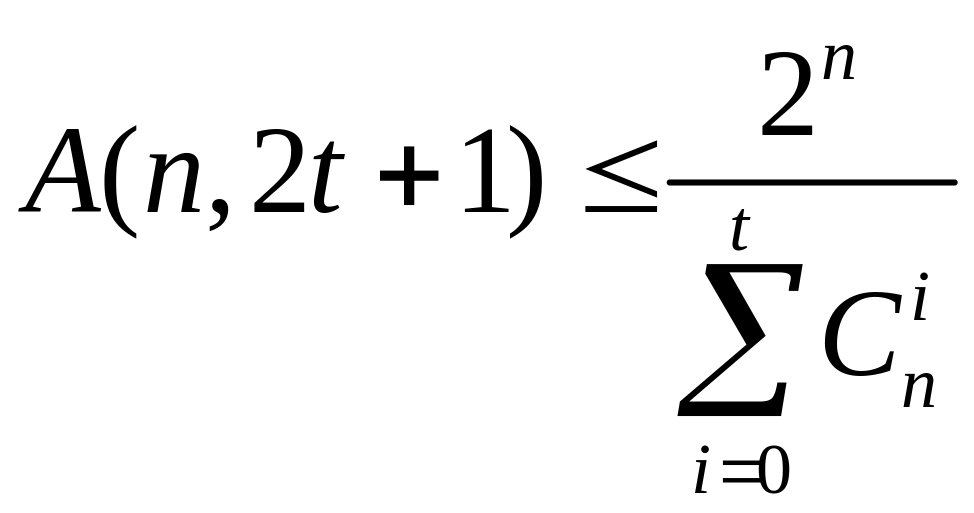
Доказательство:

Пусть V – наш код, V’ – шар радиуса t, тогда в это шаре расстояние между двумя любыми точками .

Таких множеств // // .

По определению и получим искомое неравенство.

Теорема (граница Джоши)

Доказательство:

Пусть V – код с расстоянием d, , V’ – множество всех векторов, у которых . Тогда , для любых x,y V’: .

.

Теперь получим оценку снизу.

0

0.1

0.2

0.3

0.4

0.5

d/2n

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

k/n

0.156

x

П

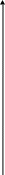
ВГ

Теорема (Варшамова-Гильберта)

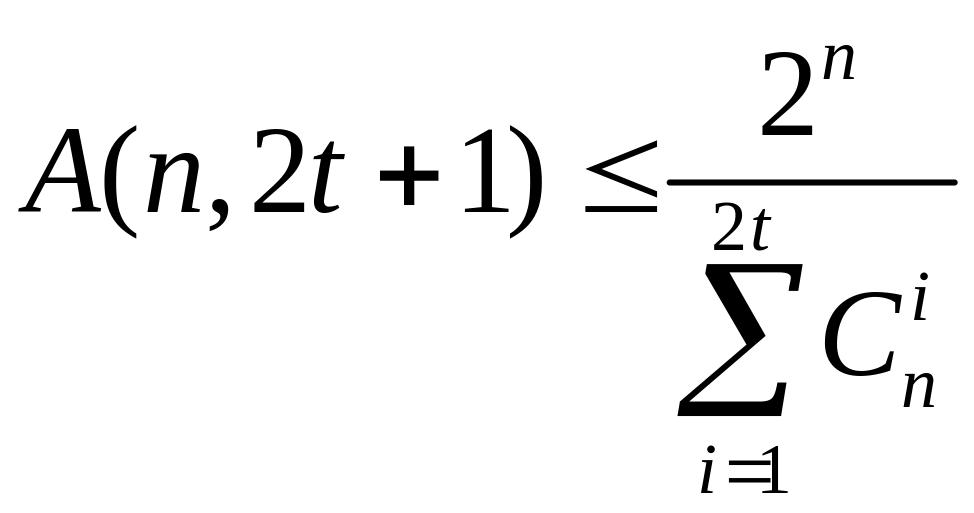
Доказательство:

Построим код V^*следующим образом:

И терации:

1. x¹ → V^*

2. x² → V^* \ S_t(x’)

… p-1 точка кода.

p) x^p → V^* \

В какой-то момент сделать это не сумеем. Расстояние между любыми точками таким образом построенного кода равняется 2t, откуда и следует неравенство.

Теорема (Плоткина)

Доказательство:

Рассмотрим код . Построим таблицу.

k₁ k₂ k_n – количество единиц в каждом столбце.

Рассмотрим сумму расстояний между всеми кодовыми словами.

Здесь каждое расстояние подсчитано 2 раза. Тогда .

max x(S-x) достигается при x = S/2. Воспользуемся этим.

( )

Хотим, чтобы . Поставим это неравенство в ( ):

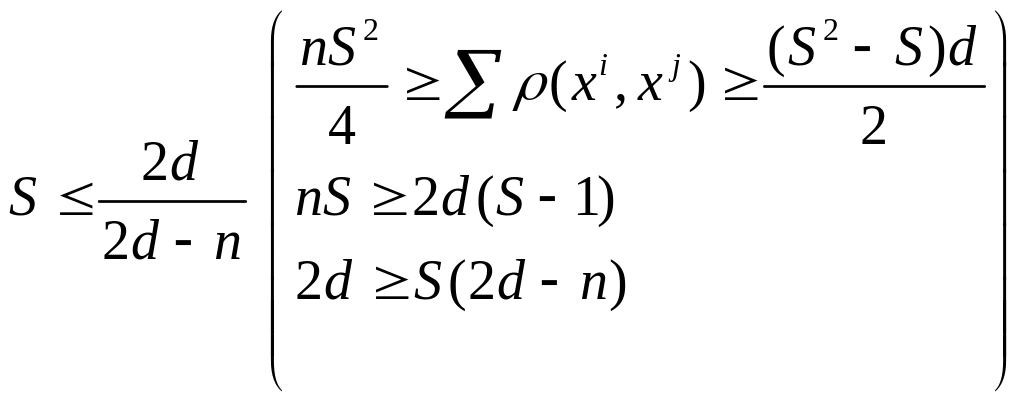
10.4Теорема Шеннона для канала с шумом.

10.4.1Факты из теории вероятности.

- случайная величина.

- мат. ожидание.

- дисперсия.

Теорема (неравенство Чебышева)

Испытание Бернулли, вероятность успеха p (неудача 1- p). Есть n испытаний. Тогда .

Доказательство:

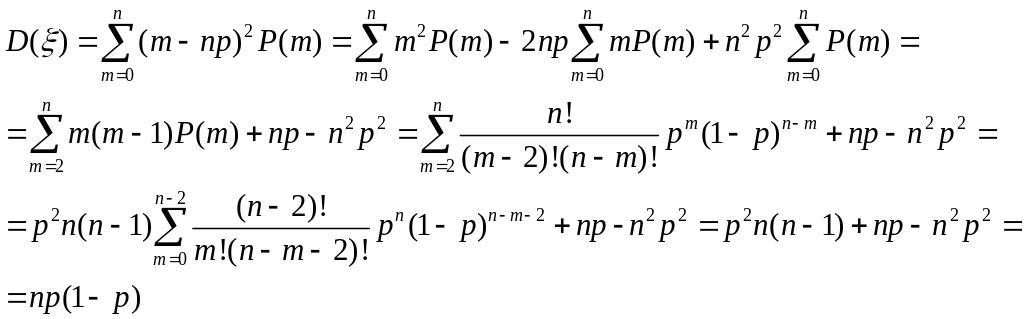
10.4.2Схема кодирования и декодирования. Вспомогательные утверждения.

Если передается слово из n 0 и 1, то - вектор, подчиняется распределению Бернулли мат. ожидание и дисперсия такого вектора считаются по доказанному выше.

1) Есть код C = {x¹…x^m} – кодовые слова

2) Применяем декодирование в ближайшее слово (по наибольшему правдоподобию)

П ередача Прием

a x¹ T(C) – таблица

b x²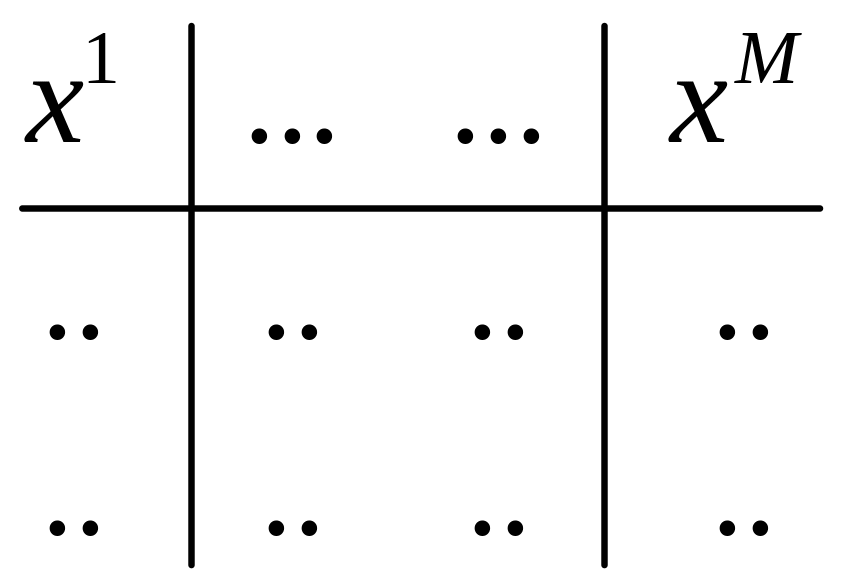

… …

… x^M

3) Вероятность ошибки декодирования

P(x) – вероятность неправильного декодирования x * Bⁿ. ∑P(x) – зависит от комбинаторных свойств кода, ошибки p, потерь в канале и т.д.

P_c (характеристика кода C) = 1\M ∑P(x)

Число различных кодов в Bⁿ: *формула* - число кодов мощности M в Bⁿ.

Пусть L – множество таких кодов. ρ(x) – вероятность правильного декодирования.

ρ_с = 1\M ∑ρ (x)

P_c + ρ_с = 1

P*(M, n, p) = min Pc → P*(M, n, p) ≤ , где P*(M, n, p) – характеристика существующего кода, являющаяся наилучшей из возможных с точки зрения ошибки декодирования.

На сегодняшний день наилучший код не найден, все существующие отличны от него в константу раз.

Лемма ( ): Возьмем точку в Bⁿ и шар S_[pn](x), оценим число точек в нем: |S_[pn](x)| ≤ 2^nH(p)

Доказательство: |S_[pn](x)| =

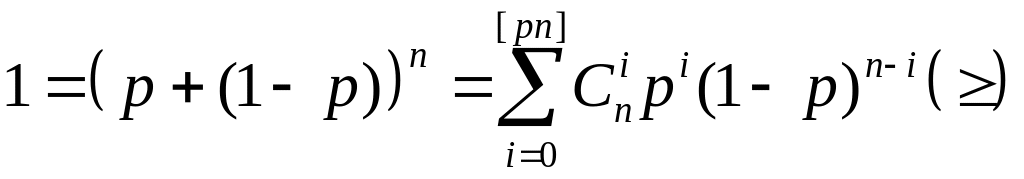
Вспомним, что 0 ≤ p < 1\2, принцип – декодирование в ближайшее, (1 – p)ⁿ ≥ p(1 – p)^n-1 ≥ … ≥ p^k(1-p)^n-k

, где - мощность.

Тогда |S_[pn](x)| ≤ (p^[pn] (1 – p) ^{n – [pn]})^-1 = = 2^nH(p)

xⁱ → канал → Y

Считаем, что Y = x_i + e, e – вектор ошибок

τ – случайная величина = |e| (количество ошибок)

Т.к. источник Бернулли, то E(τ) = np, D(τ) = np (1 – p)

b = - добавим к мат ожиданию, тогда радиус шара *формула*

Лемма ( ): P{ τ > ρ} ≤ ε\2 для любого заранее заданного ε.

Доказательство: Применим неравенство Чебышева:

P{| τ – E(τ)| > ε} ≤ D(τ)\ε²

ρ = [E(τ) + b]

P {|τ – nP| > b} ≤ D(τ) \ b²

P{| τ – nP| > b} ≤ ε\2

P(τ > ρ) = P{|τ – nP| > b} – проверим это:

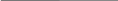
- τ np τ

τ > nP +b

τ – nP > b

Лемма ( ): Пусть ρ = [E(τ) + b] и b = формула, тогда 1\n log |S_ρ(x)| ≤ H(P) – O(n-^1\2) при n → ∞.

Доказательство: Из леммы ( ) и леммы ( ):

|S_ρ(x)| ≤ 2^nH(ρ\n) . Домножим на log и поделим на n.

1\n log |S_ρ(x)| ≤ H(ρ\n) = - ρ\n log ρ\n – (1 – ρ\n) log (1 – ρ\n) = - [nP + b]\n log [nP + b]\n – (1 – [nP + b]\n] log (1 – [nP + b]\n) ≈ -P log P – (1 – P) log (1 – P) – O(b\n) = O(n^-1\2)

1. 

2.