10Канал с шумом.

Рассмотрим теперь следующую более общую схему.

Код

Источник

F

Получатель

F^-1

Декодер

I

Декодер

II

Канал

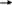
Потери информации

Избыточность

10.1Модели каналов.

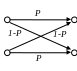1. Д воичный симметричный канал

1 1

P > 1/2

0 0

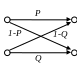2. Д воичный ассиметричный канал

1 1

P > 1/2, Q > 1/2

0 0

3. Двоичный стирающий канал

P

1

1-P

1

1-P

x – стирание

P

0 0

Пример:

Передаем 11011, p = 4/5

Для : 11001

Для II: 110х1

4. Канал с выпадением

Поскольку искаженная информация информацией не является, возникает еще один кодер и декодер: F^-1(F*(α)) = α с вероятностью (1 – ε).

Должны сделать такой механизм, чтобы если в канале произошли потери, то с вероятностью (1 – ε) декодер сможет их восстановить.

Эффективность идеи избыточности была доказана Шенноном: добавим o(H) для того, чтобы с вероятностью (1 – ε) декодировать сигнал с шумом.

Мы работаем со стационарными источниками, при других технические различия не очень велики, при смене модели вся математика меняется капитально.

10.2Передача информации по двоичному симметричному каналу с шумом

10.2.1Схема и принципы кодирования.

Вероятность ошибки p (p < 1/2).

Теперь считаем, что источник выдает двоичное слово, и в двоичном симметричном канале шум представляет собой искажение символа с вероятностью 0<p <1/2.

Источник

Bⁱ→a_i

F(Bⁱ)

0<P<1/2

F’(Bⁱ)

C

Bⁱ

Канал

F^-1(Bⁱ)

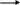
Опр. Пропускная способность канала

C(p) = 1 – H(p)

- энтропия канала.

Пусть Bⁿ - булев куб размерности n.

Опр. Кодом C называется произвольное подмножество .

Пусть M – мощность множества C.

Опр. Скорость передачи кода .

Опр. Расстояние Хемминга .

= количество различных бит в x и y.

Пусть |x| - количество единиц в ( норма x).

Опр. Кодовое расстояние .

Опр. (n,M,d)-код – это код C, такой, что |C| = M, C = {xⁱ}, xⁱ Bⁿ, d(C) = d.

Схемы кодирования могут быть самые разные. Рассмотрим одну из самых известных.

В ее основе лежит два принципа:

1. Принцип наибольшего правдоподобия. Этот принцип вытекает из очевидного соотношения

pⁿ < p^n-1(1-p) < p^n-2(1-p)² < … <(1-p)ⁿ (*)

и говорит о том, что вероятность k ошибок с кодовом слове меньше, чем вероятность s ошибок для всех s>k.

2. Принцип избыточности.

Схема кодирования по наибольшему правдоподобию

d

x¹

x²

x³

Шар Bⁿ, в нем 2ⁿ точек.

M < 2ⁿ

Стараемся, чтобы каждую из этих точек можно было окружить шаром радиуса t так, чтобы эти шары не пересекались.

pⁿ < p^n-1(1-p) < p^n-2(1-p)² < … <(1-p)ⁿ (*)

(*) следует из того, что p < 1/2.

Это значит, что вероятность того, что ошибок не будет, больше, чем того, что будет одна ошибка и т.д. Это единственное обоснование схемы кодирования по наибольшему правдоподобию.

Д ешифруем Yⁱ. В xⁱ на расстоянии 1 в шаре стоят все векторы, которые получились бы с одной ошибкой, на расстоянии 2 все векторы с двумя ошибками и т.д.

Возможны 3 случая:

1. Yⁱ оказалась в шаре с центром в xⁱ – произошло менее, чем d ошибок, ;

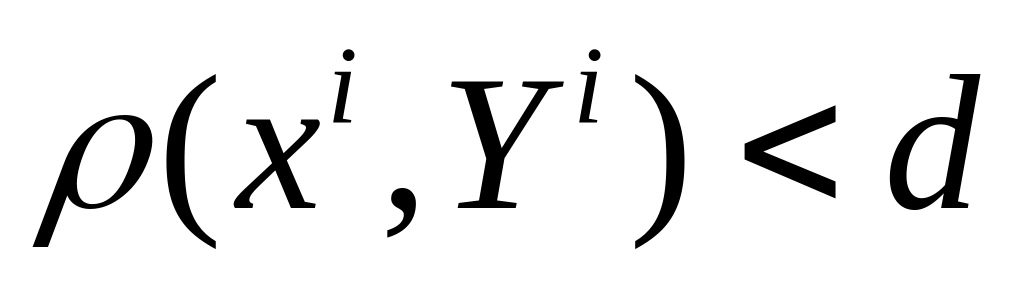2. Yⁱ не попадает ни в один из шаров, 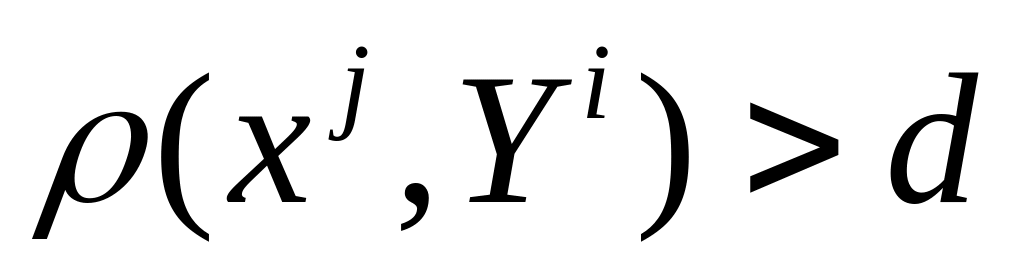для любого j;

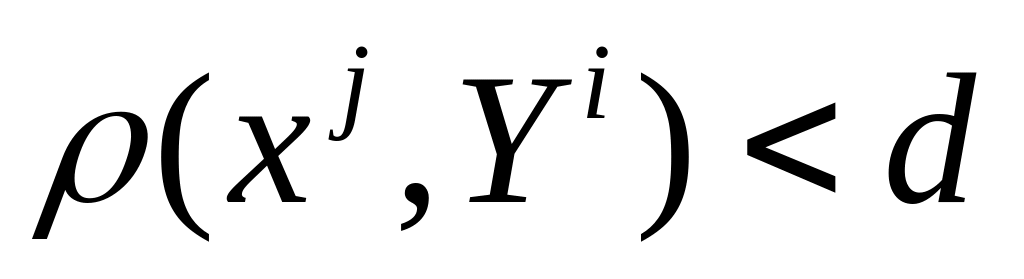3. (попала не в этот шар, а в соседний).

Если выполняется первый случай, то Yⁱ → xⁱ. Если третий, то Yⁱ → x^j, декодирование неверное.

Во втором случае обычно декодируют Yⁱ в x^j, тоже ошибка декодирования.

Пример:

C: a = 11 → x¹ = 11000

b = 00 → x² = 00110

c = 10 → x³ = 10011

d = 01 → x⁴ = 01101

11000	00110	10011	01101
11001	00111	10010	01100
11010	00100	10001	01111
11100	00010	10111	01001
10000	01110	11011	00101
01000	10110	00011	11101
11110	00000	01011	10101
01010	10100	11111	00001

Источник Кодер B⁵

a x¹

b x¹ → канал

c x¹ C – (5,4,3)-код

d x¹

|

xⁱ

x^j

d

B⁵| = 32

Если d = 2t + 1, то шары вокруг кодовых слов строим радиуса t.

Если d = 2t + 2, то шары радиуса t.

Тогда здесь каждое кодовое слово окружаем шаром радиуса 1.

Если получили любое слово из первых пяти строк таблицы, то декодирование произойдет правильно. Если же взять другое слово, то декодирование произойдет либо правильно, либо нет.

Т.о. куда отнести не вошедшее слово – часть не алгоритма декодирования, а схемы декодирования.

Код не обязан быть систематическим.