6Теорема Шеннона

Рассмотрим теперь математическую модель, являющуюся объединением двух предыдущих. Случайный источник генерирует буквы алфавита А = (а₁, … , а_n), к которым потом применяется некоторый алгоритм алфавитного кодирования φ. (Каждой букве a_i алфавита A ставится в соответствие B_i= φ(a_i) – слово длины l_i в алфавите B = (b₁, … , b_q)). Как можно оценить качество такого алгоритма?

В случае вероятностного источника такие количественные характеристики алгоритма как или уже не являются информативными, так как не зависят от вероятностей.

В этом случае удобно использовать величину , которая характеризует среднее количество букв алфавита B , приходящееся на один символ алфавита A при алфавитном кодировании ϕ. (Назовем эту величину стоимостью кодирования ϕ). Пусть теперь , где минимум берется по всем возможным дешифруемым алгоритмам алфавитного кодирования (при заданных алфавитах A и B и распределении вероятностей p₁…p_n). (Назовем эту величину минимальной стоимостью кодирования).

Если бы мы знали C(A), то смогли бы оценить качество нашего алгоритма ϕ.

Следующая теорема (она известна под названием теоремы Шеннона для канала без шума) дает ответ на этот практически важный вопрос.

Теорема. Справедливо соотношение

.

Доказательство.

1. Сначала докажем оценку снизу

.

В следующих выкладках все суммы берутся по i=1,..,n. Используется известное из математического анализа неравенство ln x x – 1, log x log e(x – 1), а также неравенство Крафта.

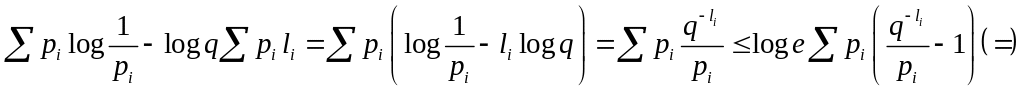
( – по неравенству Крафта, ).

2. Для доказательства оценки сверху мы построим конкретный алгоритм алфавитного кодирования ϕ (известный как алгоритм Шеннона-Фано). Ведь если оценка сверху будет выполняться для некоторого C_ϕ(A), то она будет выполняться и для C(A).

В данном коде набор длин задается следующим соотношением.

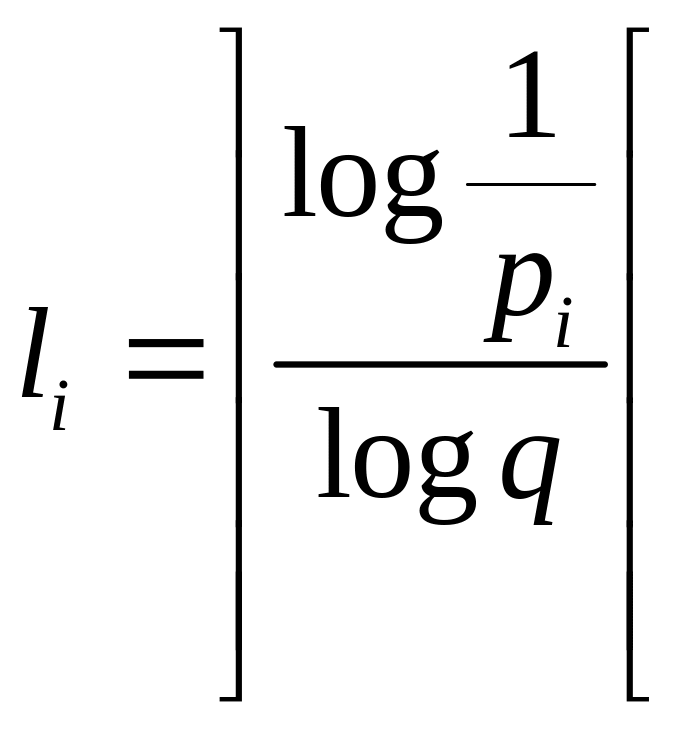(целая часть с избытком (сверху)).

Проверим, удовлетворяет ли этот набор неравенству Крафта.

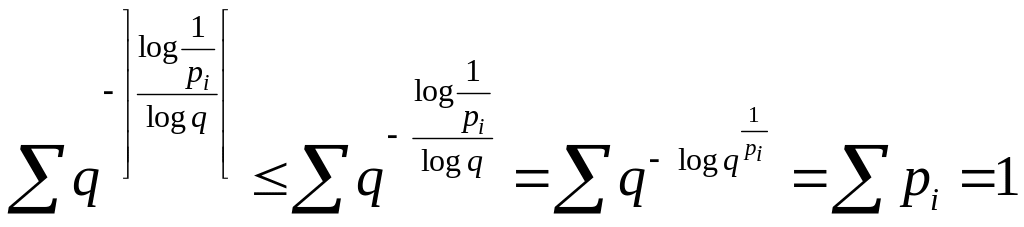
, неравенство выполняется.

Теперь построим код точно также, как это делалось выше при доказательстве теоремы о существовании префиксного кода. Оценим теперь сверху величину C_ϕ(A) для этого кода.

C_ϕ(A) = .

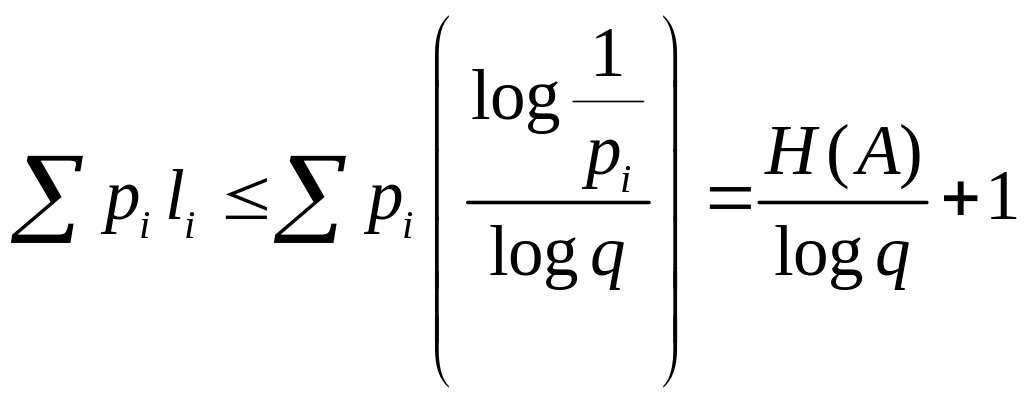Теорема доказана.

Для случая бинарного алфавита В получаем неравенство

Н(А) С(А) Н(А) + 1.

Пример. Рассмотрим алфавит А = {0,…,9}. Ниже приведены два способа префиксного дешифруемого кодирования цифр бинарными последовательностями. Первый способ – это простой перевод в двоичную запись.

I способ 0 0000 II способ: 0 000

1 0001 1 010

2 0010 2 001

3 0011 3 011

4 0100 4 100

5 0101 5 101

6 0110 6 1100

7 0111 7 1101

8 1000 8 1110

9 1001 9 1111

На рисунке по колонками приведены значения C_ϕ(A) для обоих способов в предположении, что цифры генерируются случайным источником равновероятно. Из теоремы Шеннона следует оценка

С(А) Н(А) =

Второй алгоритм дает достаточно близкий результат. (На самом деле можно показать, что для данного случайного источника С(А)=3,4. )