5.1.2Энтропия по Шеннону.

Этот теоретический предел возможного сжатия и определяется количеством информации в том слове (множестве слов) с помощью которых информация представлена.

5.1.2.1Математическая модель: алфавитное кодирование случайного источника.

Рассмотрим следующую модель. Имеется источник, который поочередно генерирует буквы алфавита A=(a₁…a_n) с вероятностями p₁…p_n. То есть имеет место следующая ситуация.

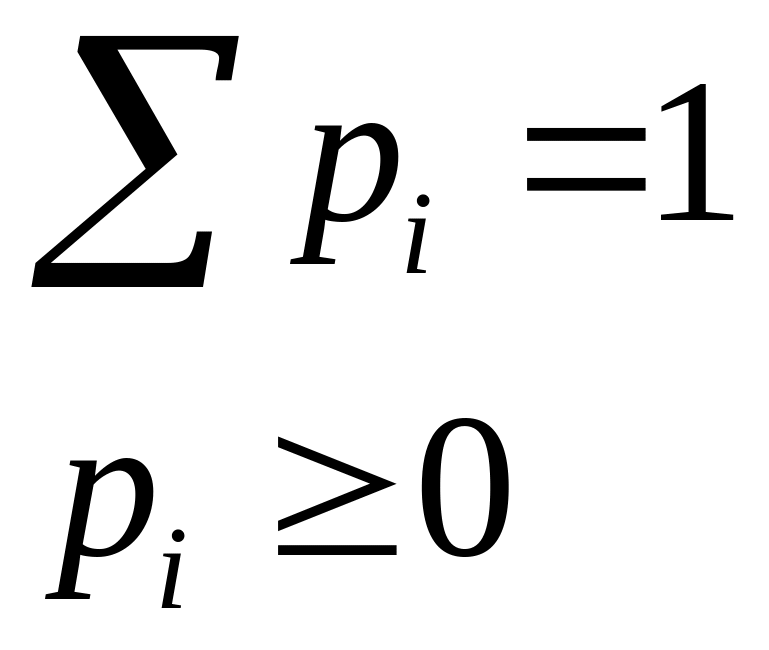
Каждая буква a_i генерируется с некоторой вероятностью p_i. Эта вероятность p_i не зависит от того, что выдал источник ранее и что он будет выдавать потом. Она также не зависит от очередности выдачи букв источником и от того, какой по счету от начала выдачи выдана данная буква. Такой источник называется источником Бернулли, что является частным случаем стационарного источника. На практике встречаются и другие источники. Для них приведенный ниже результаты неверны, но могут быть получены их аналоги.

5.1.2.2Энтропия по Шеннону

Опр. Энтропией случайного источника (энтропией Шеннона) называется число

H(A) = .

В качестве замечания приведем следующее рассмотрение, которое показывает, почему данная формула выглядит именно так.

Пусть мы хотим ввести меру µ(A), которая характеризовала бы случайный источник.

Наложим на меру ограничения:

1. µ(A) = φ(p₁…p_n)

2. µ(A) ≥ 0, µ(A) < M

3. A×A – опыт на множестве A – 2 раза. Вероятность генерации следующей буквы не зависит от предыдущей итерации. φ(n²) исходов. φ(n^k) = k φ(n)

4. φ(n) – монотонна по n

5. p₁ < … p_n = 1/n → φ(n) схожа с энтропией по Хартли.

Пусть a, n – целые неотрицательные числа.

Для любых a, n существует k: 2^k ≤ aⁿ ≤ 2^k+1

(1)

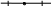
k < n log a < k+1

Применим монотонность φ к (1):

φ(2^k) ≤ φ(aⁿ) ≤ φ(2^k+1)

k φ(2) ≤ n φ(a) ≤ (k+1) φ(2)

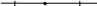
k k+1

(поделим на n и устремим к ∞)

φ(a) – φ(ε) log a → 0

φ(a) = φ(2) log a (возникает в 5 случае) – мера неопределенности

φ(n) = φ(2) log n – константа, необходимая для различия 2 элементов, полагаем ее равной 1 (отсюда и следует понятие бита)

Опыт A:

Пусть p_i – рациональные числа, p₁…p_k, n – НОК знаменателей p_i.

Тогда

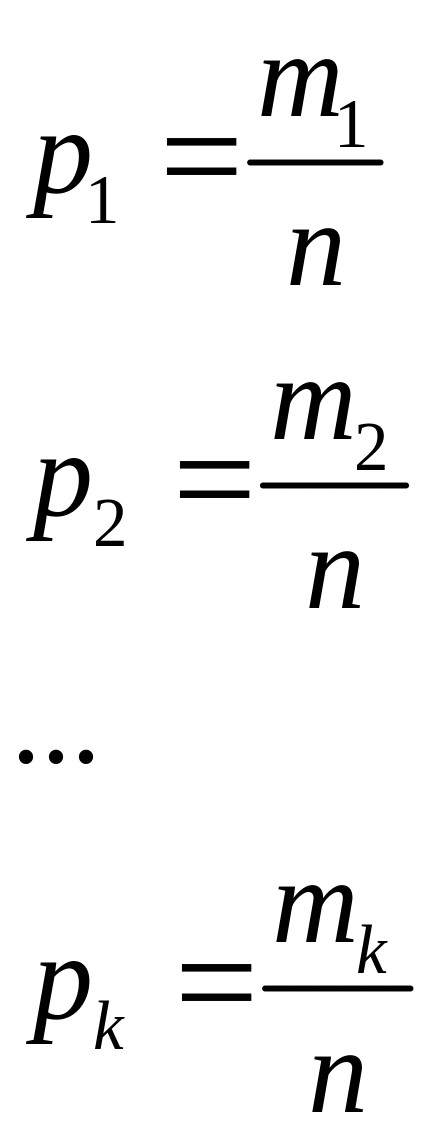
Опыт B:

n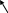 равновероятных событий разобьем на k групп .

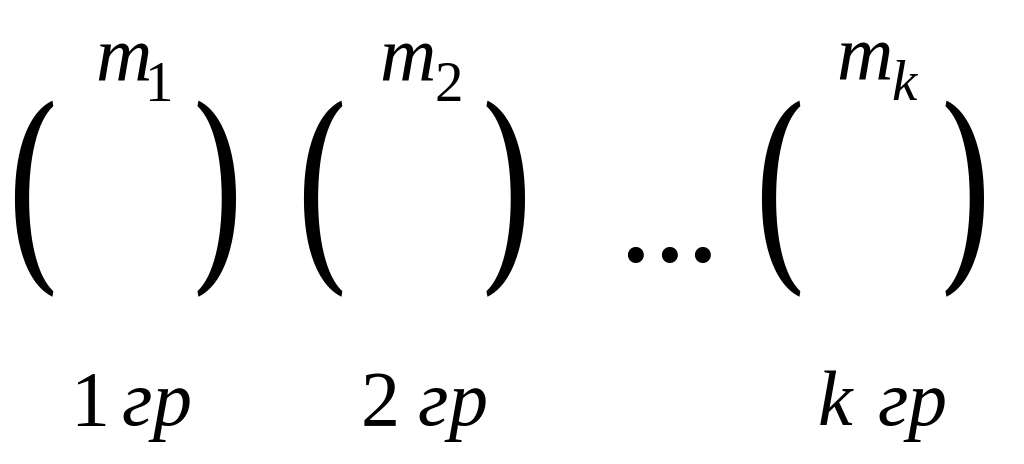Сначала определим, в какой группе необходимо исследовать события. Тогда

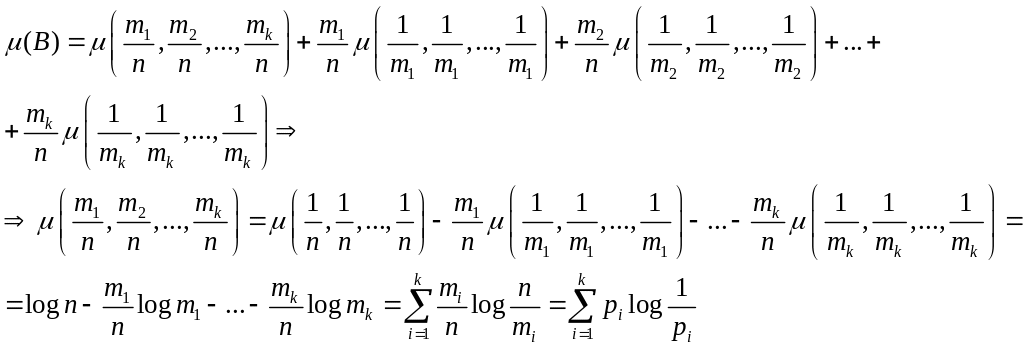
5.1.2.3Энтропия по Шеннону и энтропия по Хартли.

Заметим, что Энтропия по Хартли является частным случаем энтропии по Шеннону. Если все , то H(A) = log n , а это и есть Энтропия по Хартли множества из n элементов. В общем случае справедливо следующее утверждение, которое показывает, что энтропия по Хартли является оценкой сверху для энтропии по Шеннону. То есть ситуация равновероятных событий наихудшая с точки зрения информативности.

В следующем и других доказательствах нам потребуется математический факт, известный как неравенство Йенсена.

Неравенство Йенсена. Пусть даны числа α₁…α_n , α_i>0 , . Тогда для выпуклой вверх функции f(x) справедливо неравенство.

Теорема: Пусть имеется случайный источник, который генерирует буквы алфавита A = (a₁…a_n) с вероятностями p₁…p_n,тогда справедливо соотношение

H(A) = .

Доказательство. Рассмотрим функцию f(x) = -x log x. Так как f’(x) = - log x – 1/ln2 и f’’(x) = - 1/x , то при

x ≥ 0 функция f(x) выпукла вверх. Тогда для нее справедливо неравенство Йенсена:

Возьмем α₁…α_n , α_i>0 ,

Положим a_i = 1/n, x_i = p_i ,i=1,…,n.

H(A) =

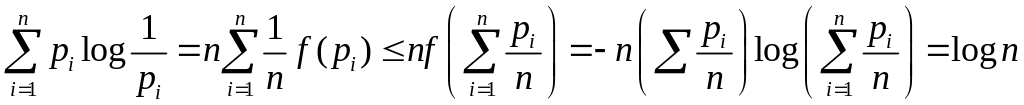
Здесь мы учли, что .

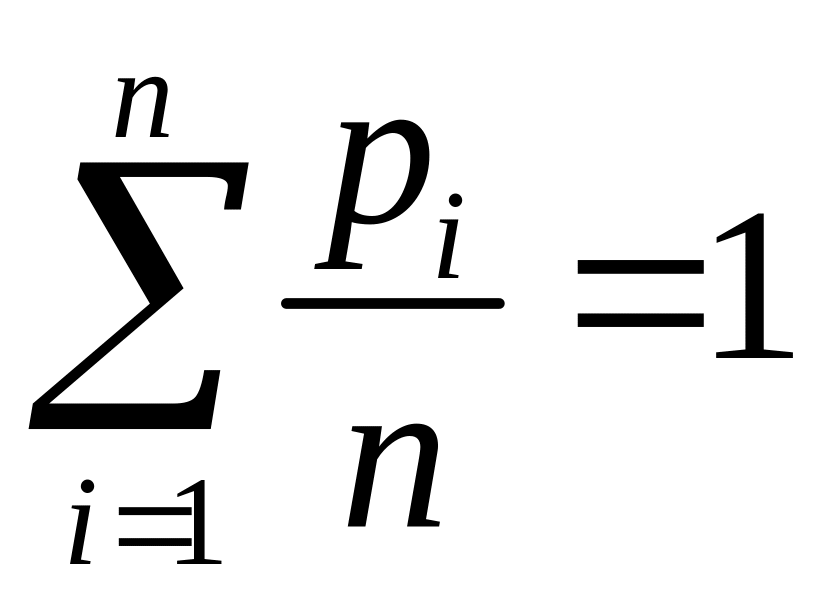Теорема доказана.