2. Компоновка лестничной клетки

Высота этажа в проектируемом здании Нэт=3300 мм, тогда высота одного марша составит (рис.3а):

Н_м= = = 1650 мм.

Размеры ступеней принимаем из расчета, чтобы двойная высота подступенка, сложенная с шириной проступи ступени, равнялась среднему шагу человека, предварительно задавшись размерами ступени 150×300мм (рис.3в) :

2∙А + В = 600÷ 640 мм;

2∙150 + 300 = 600 мм.

Окончательно принимаем ступень с размерами 150×300 мм.

Число подступенков в одном марше составит:

n_под = = = 11 шт.

Кроме этого количество ступеней должно быть в пределах 3< n=11 < 16.

Окончательно принимаем 2 марша по 11 ступеней (рис.3а,б).

Число проступей будет на единицу меньше числа подступенков, т. к. верхняя проступь совпадает с лестничной площадкой(рис.1а,б):

n_прос = n_под -1= 11-1= 10 шт.

Определим длину горизонтальной проекции лестничного марша(рис.3а,б):

l_m=n_прос∙b_ст=10∙300=3000 мм.

Определим длину лестничной клетки в свету(рис.1а,б):

L = l_m +2∙a = 3000 + 2∙1500=6000 мм,

где, a=1500мм –ширина междуэтажной лестничной площадки, принимаемой равной ширине марша.

Определим ширину лестничной клетки в свету (рис.3а,б):

В=2∙а+c=2∙1500+200=3200 мм.

где, а=1500 мм — ширина марша;

c=100….300 мм — зазор для пропуска пожарных шлангов.

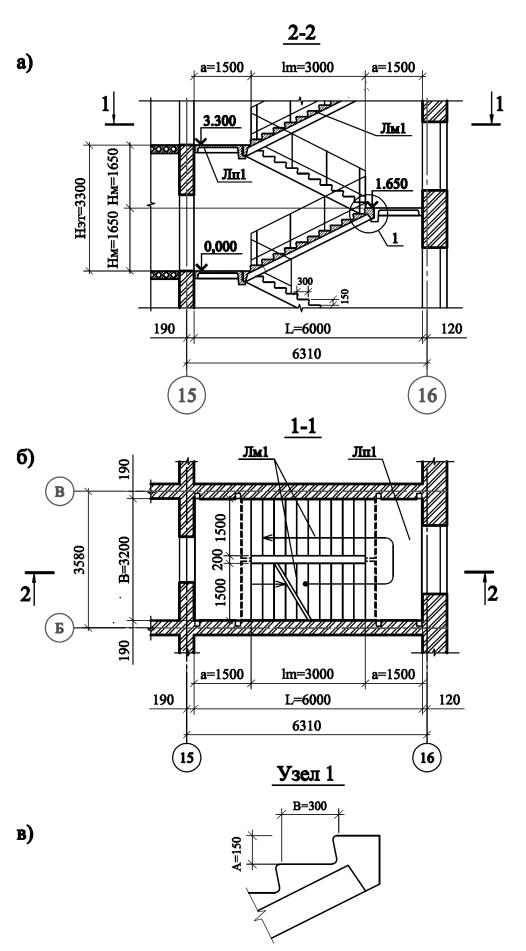
3. К компоновке лестничной клетки:

а-продольный разрез лестничной клетки; б-фрагмент плана лестничной клетки;

в-узел 1

2. Расчет и конструирование лестничного марша

   1. Предварительное назначение размеров сечения лестничного марша

Лестничный марш ребристой конструкции с фризовыми ступенями состоит из продольных ребер (косоуров), поперечных ребер (опорных), плиты монолитно связанной с ребрами и ступенями, а также ступеней –рядовых и фризовых (рис.4а,б).

Геометрические размеры рядовых ступеней h×b приняты при компоновке лестничной клетки и составляют 150×300 мм, размеры фризовых ступеней h×b принимаем равными 150×220 мм .

Определим пролет лестничного марша l₁, при конструктивной длине горизонтальной проекции l= 3440 мм и угле наклона марша α= :

l₁= = =3846 мм=3,846м,

где, α-уклон марша, характеризующийся величинами размеров ступеней и составит tg α= =0,5 => α=arctg 0.5= ; cosα=cos =0,8944

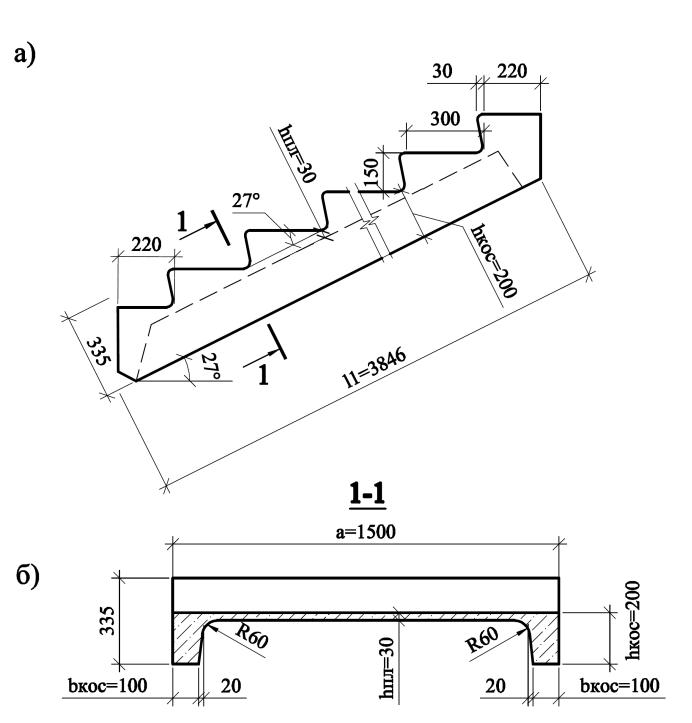
4. Лестничный марш:

а-вид сбоку; б-поперечное сечение марша

Толщина плиты между ступенями h_пл принимается равной 30 мм (рис.4а,б):

Принимаем h_пл=30 мм.

Высота продольных ребер h_кос принимается равной ( … ) пролета l₁, в пределах 150 ÷ 250 мм (рис.4а,б):

h_кос=( … )∙ l₁=h_кос=( … )∙3846=256,4…192,3мм,

Принимаем h_кос=200 мм.

Ширина продольных ребер b_кос принимаем равной (1/2…1/3) высоты косоура h_кос (рис.4а,б):

b_кос =(1/2…1/3)∙h_кос =b_кос=(1/2….1/3)∙200=100…66,7 мм

Принимаем b_кос =100 мм.

1. Определение нагрузок и внутренних усилий в марше.

На лестничный марш действуют следующие нагрузки:

• постоянная нагрузка от собственного веса марша;

• временная полезная нагрузка, которая зависит от назначения здания или сооружения, к которым примыкает марш и принимается по ДБН В.1.2-2:2006. СНБС. Нагрузки и воздействия. Нормы проектирования.

Так как плоскость действия нагрузки не совпадает с главными плоскостями сечения марша, то необходимо определить величину составляющей этой нагрузки, действующей по нормали к продольной оси марша. Для этого определим значение нагрузки на 1 горизонтальной проекции марша.

Подсчет нагрузки на 1 горизонтальной проекции лестничного марша произведем в табличной форме, анализируя их нормативные и расчетные значения раздельно.

Таблица № 1

Вид нагрузки	Характеристическое значение нагрузки, кН/	Коэффициент надежности по предельному значению нагрузки, γfm	Расчетное значение нагрузки, кН/
Постоянная нагрузка ( ): От веса ступеней 150×300 От веса плиты δ=30мм От веса косоуров за вычетом толщины плиты (h=hкос –hпл) : От ограждения и поручней: 0,2 кН/	1,875 0,838 0,696 0,2	1,1 1,1 1,1 1,1	2,06 0,922 0,766 0,22
Итого постоянная:	3,609		гор=3,968
Временная полезная нагрузка ( ) для торгового зала по ДБН В.1.2-2:2006	4	1,2	pгор =4,8
Всего: ( +p)	7,609		qгор= 8,768

Нагрузка на 1 м длины марша, действующая по нормали к его оси, с учетом коэффициента по ответственности γ_n=0,95 составит:

• расчетная полная q=q_гор ∙а∙cos α∙ γ_n =8,768∙1,5∙0,894∙0,95=11,17 кН/м

• нормативная полная q_n= ∙а∙cos α=7,609∙1,5∙0,894∙0.95=9,69 кН/м

Лестничный марш свободно опирается на консольные выступы лестничных площадок, поэтому расчетная схема марша принимается в виде однопролетной свободно опертой балки, загруженной равномерно распределенной нагрузкой q (рис.5).

Определим расчетный пролет марша при длине площадки опирания с=90мм:

l₀=l₁∙-

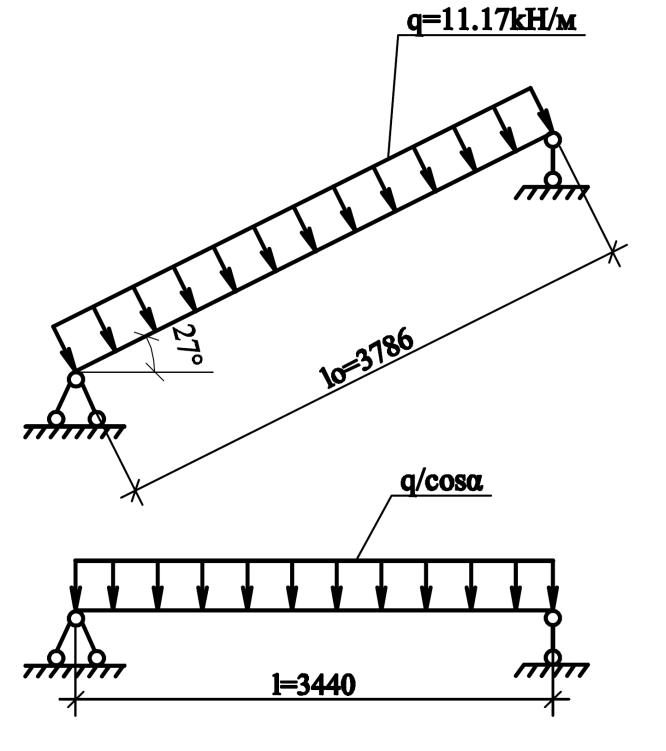
5. Расчетная схема лестничного марша

Определим усилия от расчетной нагрузки:

• изгибающий момент:

M= = = 20,01 кН∙м

• поперечная сила:

Q= = = 21,15 кН