Тема 4. Способы изучения стохастических (корреляционных) взаимосвязей в экономическом анализе

Задание 4.

Для изучения связи между зависимой и независимой величинами на базе отобранных данных:

1) постройте корреляционную таблицу, характеризующую зависимость результа­тивного признака от факторного. Сделайте выводы о характере связи между признаками;

2) изобразите связь между изучаемыми признаками графически;

3) постройте уравнение регрессии по сгруппированным данным. Параметры уравнения определите методом наименьших квадратов. Рассчитайте теоретические (полученные по уравнению регрессии) значения результативного признака. Определите форму связи между признаками;

4) на основе F-критерия Фишера и t-критерия Стьюдента проверьте значимость: в первом случае - уравнения регрессии; во втором - его параметров. Дайте экономическую интерпретацию параметров уравнения связи;

5) по сгруппированным данным вычислите линейный коэффициент корреляции и корреляционное отношение. Сделайте выводы о степени и направлении связи между изучаемыми признаками;

6) с экономической точки зрения сформулируйте выводы относительно иссле­дуемой вами связи.

Решение.

Расчетная таблица для определения параметров уравнения регрессии (парная регрессия) :

Таблица 8

N п/п	X	Прирост населения Y	X2	XY	Y2
1	10,74	-11550	115,3476	-124047	133402500	-10631,2
2	9,00	-17742	81,0	-159678	314778564	-8849,1
3	10,69	-9865	114,2761	-105456,8	97318225	-10580,0
4	10,16	-5754	103,2256	-58460,64	33108516	-10037,2
5	10,10	-9389	102,01	-94828,9	88153321	-9975,7
6	11,44	-12163	130,8736	-139144,72	147938569	-11348,1
7	11,93	-3322	142,3249	-39631,46	11035684	-11850,0
8	9,19	-9409	84,4561	-86468,71	88529281	-9043,7
9	8,75	-15031	76,65	-131521,25	2259302961	-8593,1
Итого:	92,00	94225	950,1639	-939237,53	1140195621	-939237,53

Используя таблицу 8, построим уравнение регрессии:

-846,4а₁=866870

а₁=-1024,2

92а₀ - 973157,9=-939237,5

92а₀=33920,4

а₀=368,7

Получим уравнение прямой вида:

Данные для расчетов оформим в виде таблицы.

Таблица 9

№п/п
1	-11550	-10631,2	-918,8	844193,44	-2127,5	4526256,25
2	-17742	-8849,1	-8892,9	79083670,41	-8319,5	69214080,25
3	-9865	-10580,0	715,0	511225	-442,5	195806,25
4	-5754	-10037,2	4283,2	18345802,24	3668,5	13457892,25
5	-9389	-9975,7	586,7	344216,89	33,5	1122,25
6	-12163	-11348,1	-814,9	664062,01	-2740,5	7510340,25
7	-3322	-11850,0	8528	727267,84	6100,50	37216100,25
8	-9409	-9043,7	-365,3	133444,09	13,5	182,25
9	-15031	-8593,1	-6437,9	41446556,41	-5608,5	31455272
ИТОГО:	-94225	90908,1	-3316,9	214099954,49	-9422,50	754522806

На основе t-критерия Стьюдента проверим значимость параметров уравнения регрессии.

=4877,38

Вычислим расчетные (фактические) значения t-критерия:

для параметра :

для параметра :

=1,0488

=5,0

v=n-2=9-2=7

t_табл =2,365

Вывод: т.к. t_расчt_табл, то параметры а₀ и а₁ признаются значимыми.

m – число параметров в уравнении регрессии.

_у = 9156,19

_ост = 4877,38

v₁ = m – 1=2 – 1=1

v₂ = n – m= 9 – 7=2

F_табл=5,59

Вывод: т.к. F_расч  F_табл (24,67  5,59) больше чем в 4 раза, то уравнение регрессии статистически значимо, т.е. доля вариации, обусловленная регрессией, намного превышает случайную ошибку и уравнение регрессии пригодно для практического использования.

Корреляционное отношение -  представляет собой относительную величину, получающуюся в результате сравнения среднего квадратического отклонения выровненных значений результативного признака , т.е. рассчитанных по уравнению регрессии, со средним квадратическим отклонением (фактических) значений результативного признака :

или

При линейной форме уравнения применяется показатель тесноты связи – линейный коэффициент корреляции

_X=1,0488

_Y=9156,19

Вывод: линейный коэффициент корреляции принял положительное значение, что указывает на прямую связь.

Для оценки значимости коэффициента корреляции - r используют t-критерий Стьюдента, который применяется при t-распределении, отличном от нормального.

где (n-2) – число степеней свободы при заданном уровне значимости  и объеме выборки n.

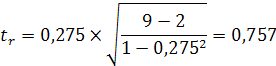
_y=9156,19

Вывод: линейный коэффициент корреляции принял положительное значение, что указывает на прямую связь.

=173,7

=172,5

_X1=1,0488

_X2=2,51

Вывод: линейный коэффициент корреляции принял отрицательное значение, что указывает на обратную связь.

Множественный коэффициент корреляции вычисляется при наличии линейной связи между результативным и несколькими факторными признаками, а также между каждой парой факторных признаков:

В случае оценки тесноты связи между Y, X₁, X₂ множественный коэффициент корреляции определяется по следующей формуле:

Задание 5.

Для изучения связи между зависимой и независимой величинами на базе отобранных данных:

1) определите результативный и не менее 2-х факторных признаков. Оцените с экономической точки зрения важность факторов и последовательность их включения в уравнение регрессии;

2) определите форму корреляционного уравнения и обоснуйте его выбор. Проанализируйте характер связей;

3) постройте расчетную таблицу для определения параметров уравнения регрес­сии. Постройте множественное уравнение регрессии. Параметры уравнения регрессии определите методом наименьших квадратов;

4) рассчитайте линейные (парные) коэффициенты корреляции, проверьте их зна­чимость. Проанализируйте характер парных зависимостей между признаками. Исключите коллинеарно связанные факторы. Рассчитайте множественный коэффициент корреляции и проверьте его значимость;

5) проверьте значимость уравнения регрессии на основе:

• F-критерия Фишера;

• Средней ошибки аппроксимации;

6) проверьте значимость коэффициентов регрессии на основе t-критерия Стьюдента.

Решение.

Результативным признаком является численность постоянного населения за 2008г, а в качестве факторных выступают прирост (разница между числом родившихся и числом умерших) и число умерших на 1000жителей, потому что два этих фактора, являются наиболее значимыми и оказывают существенное влияние на изменение (увеличение или уменьшение) численности населения.

Таблица 10

Расчетная таблица для определения параметров уравнения регрессии (множественная регрессия)

№п/п
1	-11550	10,74	18,71	-124047	115,35	133402500	200,95	350,06	-216100,50	847,9
2	-17742	9,00	20,34	-159678	81,0	314778564	183,06	413,72	-360872,28	-7458,7
3	-9865	10,69	11,94	-105456,85	114,28	97318225	127,64	142,56	-117788,10	-27284,6
4	-5754	10,16	17,16	-58460,64	103,23	33108516	174,35	294,46	-98738,64	-10486,7
5	-9389	10,10	19,65	-94828,9	102,01	88153321	198,47	386,12	-184493,85	-814,3
6	-12163	11,44	15,28	-139144,72	130,87	147938569	174,80	233,48	-185850,64	-7162,4
7	-3322	11,93	14,54	-39631,46	142,32	11035684	173,46	211,41	-48301,88	-5972,9
8	-9409	9,19	17,70	-86468,71	84,46	88529281	162,66	313,29	-166539,30	-16626
9	-15031	8,75	17,96	-131521,25	76,56	225930961	157,17	322,56	-269956,76	-19349,2
Итого:	-94225	92,00	153,28	-939237,53	950,08	1140195621	1552,54	2667,66	-1498761,95	-94306,9

Используя данные таблицы 10, построим уравнение множественной регрессии. Оно имеет вид:

Параметры уравнения регрессии определим методом наименьших квадратов, т.е. в основу этого метода положено требование минимальности сумм квадратов отклонений эмпирических данных Y_i от выровненных :

9,7a1 – 14,4a₂ = 23951,4

9,7a₁=23951,4+14,4a₂

a₁=2469,2+1,5a₂

a₁=2469,2+1,5*4091,9=8607,1

92a₀+2345986,9+(1425,2а₂+1552,5а₂)= – 939237,5

92a₀+2345986,9+2977,7а₂= – 939237,5

153,3а₀+3833433+2328,8а₂+2667,7а₂= –1498761,9

92a₀+2345986,9+2977,7а₂= –939237,5 :92 (-153,3)

– 75695,2+34,7а₂=66293,6

34,7а₂=141988,8

а₂=4091,9

9а₀+928607,1+153,34091,9= –94225

9а₀+791853,2+627288,3= –94225

9а₀= –1513366,5

а₀= –168151,8

Получим уравнение множественной регрессии:

Y_X1,X2 = –168151,8+8607,1X₁+4091,9X₂

Таблица 11

№п/п
1	-11550	-10631,2	-918,8	844193,44	-2127,5	4526256,25
2	-17742	-8849,1	-8892,9	79083670,41	-8319,5	69214080,25
3	-9865	-10580,0	715,0	511225	-442,5	195806,25
4	-5754	-10037,2	4283,2	18345802,24	3668,5	13457892,25
5	-9389	-9975,7	586,7	344216,89	33,5	1122,25
6	-12163	-11348,1	-814,9	664062,01	-2740,5	7510340,25
7	-3322	-11850,0	8528	727267,84	6100,50	37216100,25
8	-9409	-9043,7	-365,3	133444,09	13,5	182,25
9	-15031	-8593,1	-6437,9	41446556,41	-5608,5	31455272
ИТОГО:	-94225	90908,1	-3316,9	214099954,49	-9422,50	754522806

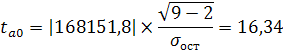
=5,0

v=n-2=9-2=7

t_табл=2,365

Вывод: т.к. t_расч t_табл, то параметры а₁ и а₀ признаются значимыми.

v₁=m-1=3-1=2

v₂=n-m=9-3=6

F_табл=5,59

Вывод: т.к. F_расчF_табл (36,785,59) более чем в 4 раза, то уравнение регрессии статистически значимо, т. е. доля вариации, обусловленная регрессией, намного превышает случайную ошибку и уравнение регрессии пригодно для практического использования.