Практична робота № 6 (2 год.)

1 Тема

Розв'язання систем нелінійних рівнянь методом ітерацій і Ньютона.

2 Мета

Ознайомитись з основними методами рішення систем нелінійних рівнянь. Придбати навички рішення за допомогою програмних засобів.

3 Обладнання: ПЕОМ

4 Порядок виконання роботи

4.1 Постановка задачі

Дана нелінійна система рівнянь

Необхідно:

1) Використовуючи метод простої ітерації, вирішити систему нелінійних рівнянь з точністю до 0,001.

2) Використовуючи метод Ньютона, вирішити систему нелінійних рівнянь з точністю до 0,001.

4.2 Математична модель задачі

4.3 Алгебраїчне розв'язання задачі

Результати обчислень звести до таблиці за зразком приведеним в теоретичних відомостях

4.4 Результати розв'язку

5 Висновок (по меті).

Теоретичні відомості

Рішення систем нелінійних рівнянь методом ітерацій і Ньютона

Зразок виконання завдання

1) Перепишемо дану систему у вигляді

Відділення коренів робимо графічно. З графіка бачимо, що система має одне рішення, розміщене в області D: 0<х<0.3; -2,2<х<-1,8.

Переконаємося в тому, що метод ітерацій може бути використаний для уточнення вирішення системи, для чого запишемо її у такому вигляді:

Так як

то в області D маємо

Таким чином, умова збіжності виконується. Обчислення проводимо за формулами

За початкові наближення приймаємо х₀=0,15, у₀=-2

n			-0,6	sin{ -0,6)	cos ,
0	0,15	-2	-0,45	-0,4350	-0,4161	-0,1384
1	0,1616	-2,035	-0,4384	-0,4245	-0,4477	-0,1492
2	0,1508	-2,0245	-0,4492	-0,4342	-0,4382	-0,1461
3	0,1539	-2,0342.	-0,4461	-0,4313	-0,4470	-0,1490
4	0,1510	-2,0313	-0,4490	-0,4341	-0,4444	-0,1481
5	0,1519	-2,0341	-0,4481	-0,4333	-0,4469	-0,1490
6	0,1510	-2,0333	-0,449	-0,4341	-0,4462	-0,1487
7	0,1513	-2,0341	-0,4487	-0,4340	-0,4469	-0,1490
8	0,1510	-2,0340

Відповідь: x=0,151; y= -2,034.

2) Відділення коренів робимо графічно. Для побудови графіків функцій складемо таблицю значень функцій у₁ і у₂, що входять в перше і друге рівняння (табл.I).

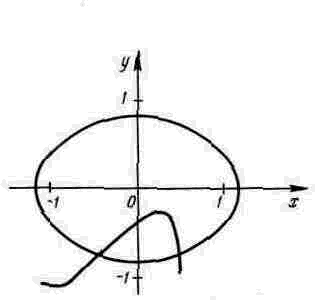
Таблиця 1

x	-1,1	-1	-0,8	-0,6	-0,2	-0,4	0	0,2	0,4	0,5
	1,21	1	0,64	0,36	0,04	0,16	0	0,04	0,16	0,25
0,8	0,97	0,8	0,51	0,29	0,032	0.13	0	0,032	0,13	0,2
1-0,8	0,03	0,2	0,49	0,71	0,97	0,87	1	0,97	0,87	0,8
	0,02	0,13	0,33	0,47	0,65	0,58	0,67	0,65	0,58	0,53
	±0,14	±0,36	±0,57	±0,69	±0,81	±0,76	±0,82	±0,81	±0,76	±0,73
1,2х	-1,32	-1,2	-0,96	-0,72	-0,24	-0,48	0	0,24	0,48	0,6
0,4+1,2х	-0,92	-0,8	-0,56	-0,32	0,16	-0,08	0,4	0,64	0,88	1
2х-у	-1,17	-0,93	-0,59	-0,33	0,16	-0,08	0,41	0,69	2,06 1,08	1,57
	-1,03	-1,07	-1,01	-0,87	-0,56	-0,72	-0,41	-0,29	-1,26 -1,28	-0,57

Значення для х можна брати виходячи з таких умов: з першого рівняння

, тобто з другого рівняння , тобто - Таким чином, . Система має два рішення. Уточнимо одне з них, що належить області D: 0,4<х<0,5; -0,76<у<-0,73. За початкове наближення приймемо х₀=0,4; у₀=-0,75. Маємо

Уточнення коріння проводимо методом Ньютона: