1. Способ вспомогательной прямой и проецирующей плоскости

Через заданную точку А проводим вертикальную проецирующую плоскость и вспомогательную прямую АВ (фронтальная проекция не указана), перпендикулярную картинной плоскости (рисунок 29).

Рисунок 29

Плоскость Σ пересекает основание картины в точке 1, которую переносим в перспективу (рисунок 30). Перспектива плоскости Σ представляет вертикальную прямую, проходящую через точку 1. Вспомогательную прямую А2 строим в перспективе при помощи точки схода Р и картинного следа 2. Высота точки 2 равна высоте точки А. Построив перспективу 2'Р и вторичную проекцию 2'₁Р вспомогательной прямой, получим в точках их пересечения с плоскостью Σ перспективу точки А и ее вторичную проекцию.

В качестве вспомогательной прямой можно взять любую горизонтальную прямую с учетом, однако, простоты построения ее перспективы.

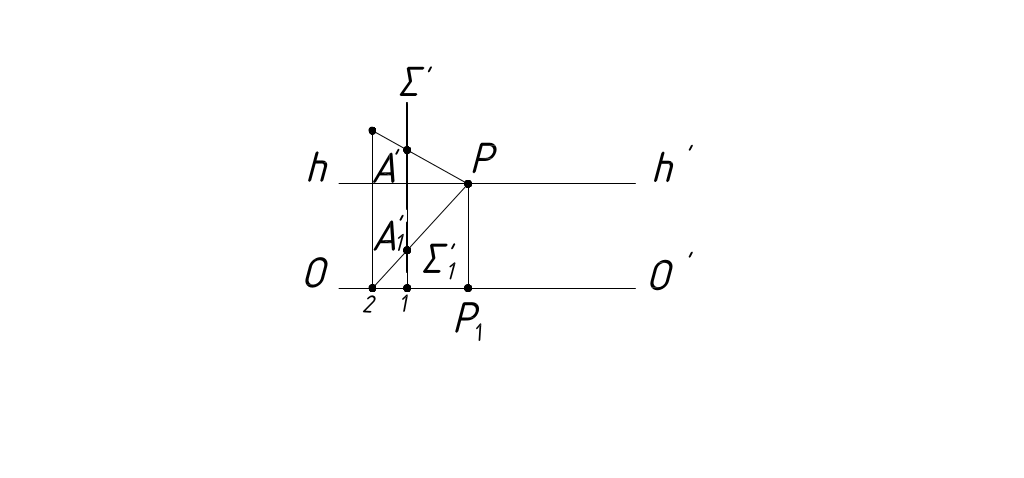
Рисунок 30

2. Метод архитекторов

Этот метод основан на использовании точек схода основных направлений горизонтальных прямых предмета, вертикальных центрально-проецирующих плоскостей, картинных следов горизонтальных прямых.

Построение перспективы геометрического тела или здания методом архитекторов обычно начинают с построения перспективы его основания, расположенного в предметной плоскости (часто с применением опущенного плана), после чего строят перспективу. Такой порядок облегчает ориентировку в перспективе, в особенности при изображении сложных объектов.

ВЫБОР ТОЧКИ ЗРЕНИЯ И ПОЛОЖЕНИЯ КАРТИННОЙ ПЛОСКОСТИ

Для того, чтобы обеспечить удачное перспективное изображение предмета, рекомендуется руководствоваться следующими правилами, выработанными практикой (рисунок 31)

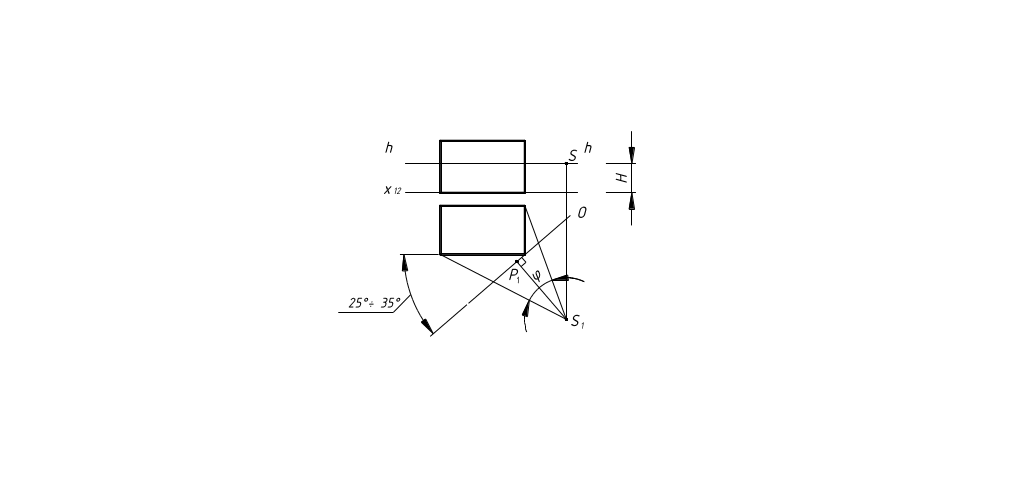
Рисунок 31

1.Угол между проецирующими прямыми, направленными в крайние точки плана предмета, называется углом зрения. Угол зрения φ следует выбирать в пределах 18° < φ < 53°. Оптимальное значение угла зрения равно 28° ( в учебной практике 38° - 40°).

2. Картинную плоскость ориентируют так, чтобы, во-первых, главная точка Р оказалась в пределах средней трети угла зрения, во-вторых, картинная плоскость составила с главным фасадом угол 25° - 35°. Боковой фасад при этом получает сильное перспективное сокращение, и изображение в целом получается более выразительным. Целесообразно картинную плоскость совместить с одним из ребер здания или сооружения, которое на перспективе изобразится в натуральную величину.

3. Высоту горизонта обычно принимают на уровне глаз человека, стоящего на земле, т.е. Н = 1,5 – 1,7 м. В том случае, если здание или сооружение имеет в плане сложную форму или при построении перспективы застройки участка, высоту точки зрения принимают до 100 м и более. Такую перспективу называют перспективой с «высоты птичьего полета».

Рассмотрим пример построения перспективы методом архитекторов.

Необходимо построить перспективу условного здания, заданного в ортогональных проекциях (рисунок 32, 33).

1. На горизонтальной проекции проводим через точку зрения S вертикальные центрально-проецирующие плоскости, проходящие через вертикальные ребра здания. Точки пересечения 1, 4, 5 этих плоскостей с основанием картины переносим в перспективу и проводим через них вертикальные линии. Продолжаем прямые СD и КD до пересечения с картинной плоскостью в точках 2 и 3. Точки 2 и 3 тоже переносим в перспективу. Точка А принадлежит картине, и ее переносим в перспективу (рисунок 33).

2. На горизонтальной проекции проводим прямые SF₁ и SF₂, параллельные сторонам основания здания, до пересечения с основанием картины в точках F₁ и F₂ – это точки схода горизонтальных прямых двух направлений. Точки F₁ и F₂ в перспективе находим на линии горизонта, откладывая их расстояния от главной точки Р (рисунок 33).

3. Начиная от точек А, 2, 3 строим перспективу вторичной проекции здания с помощью точек схода F₁ и F₂ и вертикальных прямых, проведенных через точки 1, 4 и 5.

4. Строим перспективу ребра А, откладывая от точки А вверх натуральную величину этого ребра.

5. Строим перспективу ребра D, откладывая натуральную высоту в точке 3.

6. Дальнейшие построения заключаются в проведении горизонтальных прямых, идущих в точки схода F₁ и F₂.

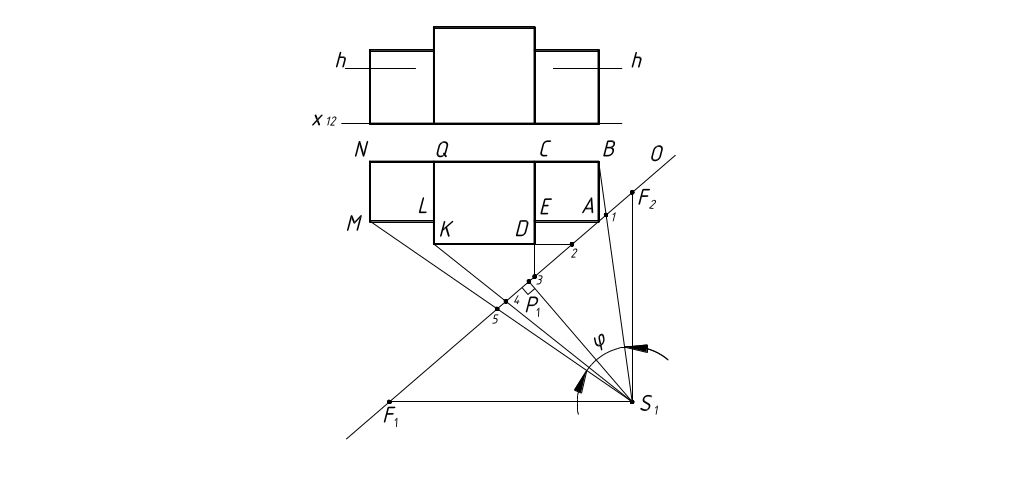
Рисунок 32

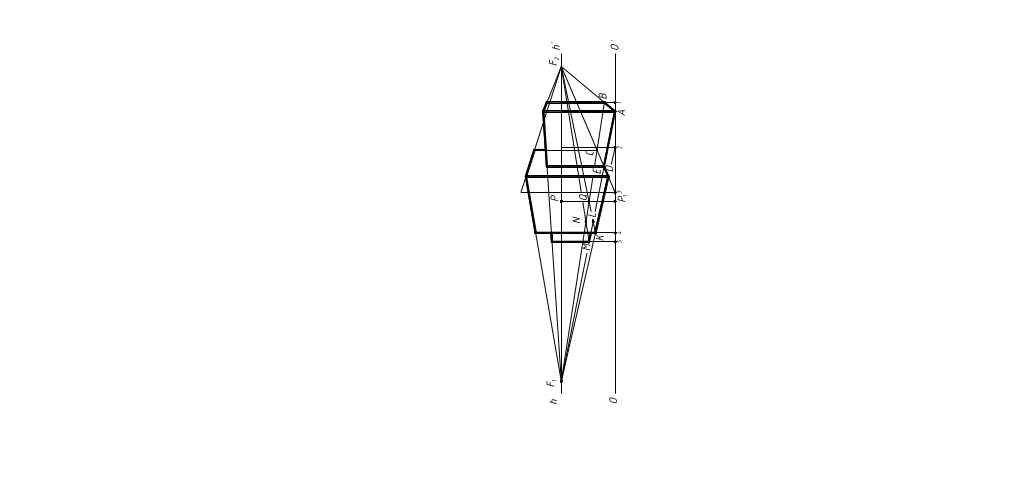
Рисунок 33

ПОСТРОЕНИЕ ОПУЩЕННОГО ПЛАНА

При сложных планах зданий и сооружений их перспективу строят с «опущенным планом». Для этого параллельно основанию картинной плоскости проводим опущенное основание картинной плоскости и строим вторичную проекцию (опущенный план) здания при заданном положении линии горизонта hh. Опущенный план представляет более раскрытую фигуру, чем основной план. Кроме того, применение опущенного плана дает возможность многие вспомогательные построения вместе с планом вынести за пределы поля перспективного изображения.

Рассмотрим пример построения перспективы с применением опущенного плана.

ПОДГОТОВИТЕЛЬНЫЕ ПОСТРОЕНИЯ В ОРТОГОНАЛЬНЫХ ПРОЕКЦИЯХ

1. Проводим картинную плоскость через ребро здания А.

2. Выбираем положение точки зрения (S₁), находим главную точку Р (P₁).

3. Определяем точки схода F₁ и F₂.

4. Через характерные точки плана здания и через точку зрения S (S₁) проводим центрально-проецирующие плоскости и определяем точки пересечения их с основанием картины OO' (точки 1,2,3,4).

5. Определяем в необходимом количестве картинные следы продолженных линий плана (точки 5,6,7,8,9,10,11,12).

Эти построения показаны на рисунке 34 а).

ПОДГОТОВИТЕЛЬНЫЕ ПОСТРОЕНИЯ В ПЕРСПЕКТИВЕ

1. Выбор размеров перспективного изображения. Так как ортогональные проекции условного дома в мелком масштабе, а перспективу желательно получить крупнее, то необходимо все размеры в перспективе пропорционально увеличить в три раза, на рисунке 34 (2:1).

2. Построение основных элементов картины. Выбираем положение главной точки Р и проводим через нее линию горизонта hh'. На линии горизонта определяем положение точек схода F₁ и F₂, перенося из ортогональных проекций их увеличенные в трое (на рисунке 34 б в два раза) расстояния от главной точки Р. Если лист чертежа имеет недостаточные размеры, его следует временно надставить с одной или с двух сторон.

Ниже линии горизонта, на расстоянии от нее, равном утроенной высоте точки зрения S, проводим основание картины О. На нем определяем основание Р₁ главной точки Р.

3. Для построения опущенного плана проводим опущенное основание картины ОO' на произвольном расстоянии от линии горизонта, сообразуясь с размерами листа чертежа. Определяем опущенное основание Р₁ главной точки Р (рисунок 34 б).

Рисунок 34

ПОСТРОЕНИЕ ОПУЩЕННОГО ПЛАНА

1. На опущенное основание картины переносим из ортогональных проекций картинные следы линий плана здания (точки А,5,6,7, 8, 9), увеличивая втрое расстояния до этих точек от точки Р.

2. Переносим на опущенное основание картины точки (1,2,3,4) пересечения центрально-проецирующих плоскостей с основанием картины и проводим через них вертикальные прямые.

3. Соединяем картинный след А с точками схода F₁ и F₂, картинные следы 5, 9, 10 – с F₁, а 6, 7, 8 – с F₂.

4. На пересечении АF₁ с вертикальной линией, проходящей через точку 2, находим точку С, также находим точки L, III, VII. Точки D, М, IV, VIII находим на пересечении горизонтальных линий плана.

5. Линии VI – IХ и II – ХI, определяющие линии коньков крыши, находим как линии, проходящие через точки пересечения диагоналей планов крыш в точки схода F₁ и F₂ .

ПОСТРОЕНИЕ ПЕРСПЕКТИВЫ ЗДАНИЯ

1. План здания строится также, как и соответствующие линии опущенного плана, т.е. при помощи картинных следов, точек схода F₁ и F₂ , вертикальных линий, проходящих через соответствующие точки опущенного плана.

2. Крыша. Перспективу точки А, расположено на плоскости картины, определяем непосредственным откладыванием утроенной высоты от А'₁. Далее при помощи точек схода F₁ и F₂ и на одной линии связи со вторичными проекциями находим точки С', D', Е', L'. Перспективы точек В, II находим при помощи картинного следа 11, а К и VI – при помощи картинного следа 12. Свесы крыш строим при помощи картинных следов 6 и 9. Точку пересечения ХI конька II 13 со скатом крыши V VI IХ Х находим при помощи вспомогательной секущей плоскости Σ, как точку пересечения прямой с плоскостью, соединяя точки IV и ХI, находим линию пересечения скатов крыш.