Вынужденные колебания струны, закрепленной на концах.

Рассмотрим колебания струны длины l, закрепленной на концах, под действием внешней силы f(x,t), рассчитанной на единицу длины. Эта задача приводит к решению уравнения

(1)

при граничных условиях

(2)

и начальных условиях

. (3)

Будем искать решение в виде

(4)

где v(x,t) – решение неоднородного уравнения

(5)

при граничных условиях

(6)

и начальных условиях

, (7)

а w(x,t) – решение однородного уравнения

(8)

при граничных условиях

(9)

и начальных условиях

, (10)

Решение v(x,t) представляет вынужденные колебания струны, т.е. такие колебания, которые совершаются под действием внешней возмущающей силы f(x,t), а решение w(x,t) – свободные колебания (было найдено в предыдущем пункте). Для нахождения v(x,t) применим метод разложения по собственным функциям. Решение будет иметь вид:

(11)

где - собственные функции однородной краевой задачи.

Определим функции T_k (k=1, 2,…). Подставив v(x,t) в виде (11) в (5), получим

(12)

Разложим функцию f(x,t) в интервале (0,l) в ряд Фурье по синусам

(13)

где

(14)

Сравнивая разложения (12) и (13) для одной и той же функции получим дифференциальные уравнения

. (15)

Чтобы решение v(x,t), определяемое рядом (11), удовлетворяло нулевым начальным условиям, достаточно подчинить функции T_k(t) условиям

. (16)

Пользуясь методом вариации постоянных, получим, что решения уравнений (15) при условиях (16) имеют вид

(17)

где f_k(t) определяются по формулам (14).

Подставив T_k(t) в (11), получим решение v(x,t).

Тогда решение u(x,t) задачи (1) – (3)

где T_k(t) определяется по (17), а

Примеры:

1. Решить смешанную задачу

Решение: Ищем в виде

(*)

откуда

В силу начальных условий

откуда

Таким образом для T₁(t) имеем

(**)

(***)

Выпишем общее решение уравнения (**)

Потребовав выполнения начальных условий (***), находим с₁=0, с₂= -1, так что

Для n>1

Пользуясь формулой (*) находим решение

2. Найти вынужденные колебания струны без начальных смещений и скорости, если на струну действует равномерно распределенная сила , зависящая от времени.

3. 

4. 

5. 

6. 

Лекция 11. Тема: Вынужденные колебания струны с подвижными концами.

Рассмотрим колебания струны длины l, под действием внешней силы f(x,t), рассчитанной на единицу длины, причем концы струны не закреплены, а двигаются по заданному закону. Эта задача приводит к решению уравнения

(1)

при граничных условиях

(2)

и начальных условиях

. (3)

К решению этой задачи метод Фурье непосредственно не применим. Однако, эта задача сводиться к задаче с нулевыми граничными условиями. Для этого введем вспомогательную функцию

(4)

Легко видеть, что

(5)

Таким образом, функция w(x,t) на концах отрезка удовлетворяет условиям (2), а внутри этого отрезка она линейна по х (рис. 1). Говорят, что функция w(x,t) продолжает граничные условия в интервале 0<x<l.

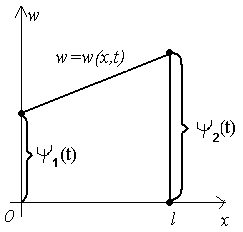
рис. 1

Решение задачи (1) – (3) ищем в виде

где v(x,t) – новая неизвестная функция.

В силу выбора функции w(x,t) функция v=u-w удовлетворяет нулевым граничным условиям

(7)

и начальным условиям

. (8)

Подставив u=v+w в уравнение (1), получим

или, учитывая выражение для w(x,t),

,

где

.

Таким образом, при приходим к смешанной задаче с нулевыми граничными условиями для функции v(x,t): найти решение уравнения

с граничными условиями

и начальными условиями

.

Пример:

Решение: Вводим вспомогательную функцию

Решение исходной задачи будем искать в виде

(*)

где v(x,t) – новая неизвестная функция.

Для нее получаем уравнение

(I)

граничные условия

(II)

начальные условия

(III)

Задача (I) – (II) имеет очевидное решение v(x,t)=0, и это единственное решение. Тогда по формуле (*) получаем решение исходной задачи