фКдержание.

Лекция №6 2

Тема: Классификация дифференциальных уравнений с частными производными второго порядка. 2

Лекция 7 10

Тема: Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. 10

Лекция 8 14

Тема: Основные уравнения и постановка задач математической физики. 14

Лекция 9 20

Тема: Постановка краевых задач. Решение задачи Коши. 20

Лекция 10 27

Тема: Свободные колебания однородной струны, закрепленной на концах. Метод Фурье. 27

Лекция 11. 36

Тема: Вынужденные колебания струны с подвижными концами. 36

Лекция 12. 44

Тема: Колебания круглой мембраны. Применение преобразований Лапласа к решению смешанной задачи. 44

Лекция 13. 50

Тема: Уравнение теплопроводности. Задача Коши для уравнения теплопроводности. 50

Лекция 14. 56

Тема: Метод Фурье для уравнения теплопроводности. 56

Лекция 15. 63

Тема: Метод Фурье для уравнения теплопроводности. 63

Лекция 16. 70

Тема: Неоднородные уравнения теплопроводности. 70

Лекция 17. 77

Тема: Уравнение Лапласа. 77

Лекция 18. 79

Тема: Решение задачи Дирихле для круга методом Фурье. Интеграл Пуассона. 79

Лекция №6 Тема: Классификация дифференциальных уравнений с частными производными второго порядка.

Определение: Уравнением с частными производными второго порядка с двумя независимыми переменными называется соотношением между независимой функцией и ее частными производными второго порядка включительно:

(1)

Аналогично записывается и для большего числа независимых переменных.

Определение: Уравнение называется линейным относительно старших производных, если оно имеет вид

(2)

где являются функциями и .

Определение: Если зависят не только от х и , а являются функциями , то такое уравнение называется квазилинейным.

Определение: Уравнение называется линейным, если оно линейно как относительно старших производных , так и относительно функции и ее первых производных :

(3)

где - функции только от и .

Определение: Если коэффициенты уравнения (3) независимы от и , то оно представляет линейное уравнение с постоянными коэффициентами.

Определение: Если , то уравнение называется однородным.

Далее рассмотрим упрощения, т.е. приведения к каноническим (простейшим) формам.

С помощью преобразования переменных

,

допускающего обратное преобразование, мы получаем новое уравнение, эквивалентное искомому,

Естественно поставить вопрос «Как выбирать , чтобы уравнение в этих переменных имело наиболее простую форму?»

. Рассмотрим линейное уравнение относительно старших производных (1).

Преобразуя производные к новым переменным, получаем

(4)

Подставляем (4) в уравнение (1), будем иметь

(5)

где

,

а функция не зависит от вторых производных.

Замечание: Если исходное уравнение линейно, т.е.

,

то

,

т.е. уравнение остается линейным.

Выберем переменные и так, чтобы коэффициент был равен нулю. Рассмотрим уравнение с частными производными первого порядка.

(6)

Пусть какое-нибудь частное решение этого уравнения.

Если положить , то коэффициент . Таким образом, упомянутая выше задача о выборе новых независимых переменных связана с решением уравнения (6).

Лемма: 1. Если является частным решением уравнения , то соотношение представляет собой общий интеграл обыкновенного дифференцированного уравнения

(7)

2. Если представляет собой общий интеграл обыкновенно дифференцированного уравнения , то функция удовлетворяет уравнению (6).

Доказательство см. Тихонов А.Н., Самарский А.А.

Определение: Уравнение (7) называется характеристическим для уравнения (1), а его интегралы – характеристиками.

Полагая , где есть общий интеграл уравнения (7), мы обращаем в нуль коэффициент при .

Если является другим общим интегралом уравнения (7), независимым от , то полагая , мы обратим в нуль и коэффициент при , т.е. .

Уравнение (7) распадается на два уравнения:

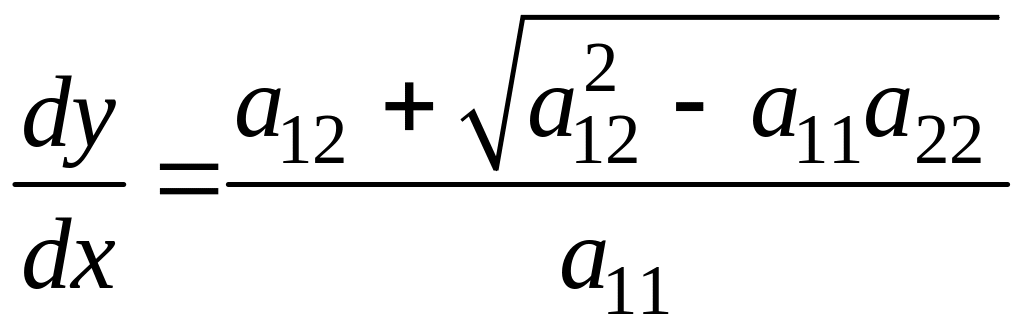(8)

(9)

Знак подкоренного выражения определяет тип уравнения (1).

Это уравнение мы будем называть в точке М уравнением

• гиперболического типа, если ,

• параболического типа, если ,

• эллиптического типа, если .

Нетрудно убедиться в правильном соотношении , где , из которого следует инвариантность уравнения при преобразовании переменных.

В размеченных точках области определения уравнения может принадлежать различным типам.

Пример: Уравнения

и

- гиперболические при всех х и у, уравнение

- параболическое при всех х и у,

- эллиптическое при всех х и у,

- эллиптическое при y>0, параболическое на линии у=0 и гиперболическое в полуплоскости y<0.