Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

Ярославский государственный технический университет

Кафедра «Кибернетика»

Отчет защищен

с оценкой

Преподаватель

Василькова Н.Н.

Исследование методов интерполяции и аппроксимации

Отчет о лабораторной работе №1

по курсу “Компьютерные технологии вычислений

в математическом моделировании”

ЯГТУ 220301.65-001 ЛР

Отчет выполнили

студенты гр. МА-33

Савинская Ю.А.

Рощина Е.А.

2009

Часть 1. Интерполяция

Цель работы:

Проанализировать для каждого из представленных методов интерполяции влияние числа узлов интерполяции на точность предсказания функции в одной точке, а также влияние положения точки прогноза на точность интерполяции. Провести сравнительный анализ методов.

1. Основная задача интерполяции – нахождение значения таблично заданной функции в тех точках внутри данного интервала, где она не задана. Решением этой задачи является построение интерполяционной функции L(x), приближенно заменяющей таблично заданную и проходящей через все заданные точки.

Метод Лагранжа состоит в построении интерполяционного полинома n-го порядка при наличии n+1 узла интерполяции.

, где

Метод Ньютона использует понятие конечных разностей

, где

Метод Чебышева для повышения точности располагает узлы по определенному закону

2.1. Моделирующая функция № 8

Параметры плавной функции: A=1, B=2, C=2, D=3

Вид функции:

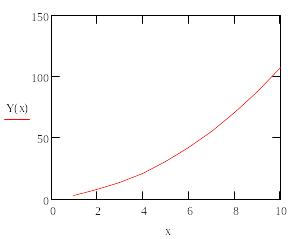
Рисунок 1. Моделирующая функция

Интервал:

2.2. Моделирующая функция № 3

Параметры изогнутой функции: A=1, B=4, C=1, D=2.

Вид функции:

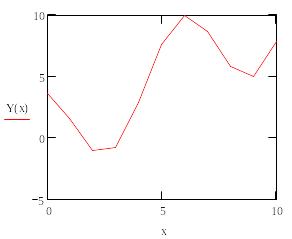
Рисунок 2. Моделирующая функция

3. Исследование влияния числа узлов на точность прогноза функции

3.1 Исследование функции:

3.1.1 По методу Лагранжа:

n	1	2	3	4	5	6	7	8
	-15,72	0,856	0,2	0,013	-0,0088	0,0009	0,043	0,0016
	-22,86	0,0695	-0,12	-0,01	0,0076	0,0005	0,0004	0,0004
	-15,90	-0,38	0,11	-0,02	-0,0028	0,002	0,0004	-0,0008

3.1.2 По методу Ньютона:

n	1	2	3	4	5	6	7	8
	-15,72	0,856	0,2	0,013	-0,0088	0,0009	0,043	0,0016
	-22,86	0,0695	-0,12	-0,01	0,0076	0,0005	0,0004	0,0004
	-15,90	-0,38	0,11	-0,02	-0,0028	0,002	0,0004	-0,0008

3.1.3 По методу Ньютона:

n	1	2	3	4	5	6	7	8
	-5,02	0,6196	0,2365	-0,0933	-0,1875	-0,0985	0,0292	0,0863
	-11,728	0,0519	-0,2118	-0.0339	0,097	0,0248	-0,0539	-0,194
	-4,2032	-0,2309	0,1045	0,0098	-0,0556	0,0417	-0,005	-0,0209

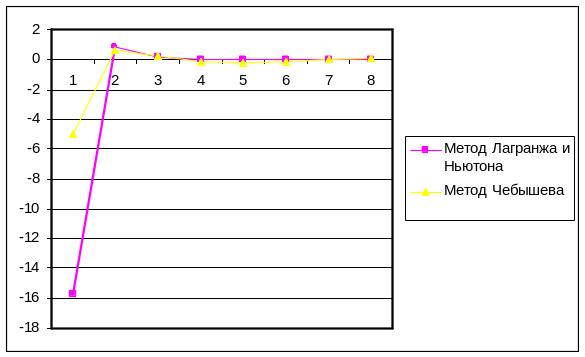
Рисунок 3. График зависимости R(x)=f(n) для точки

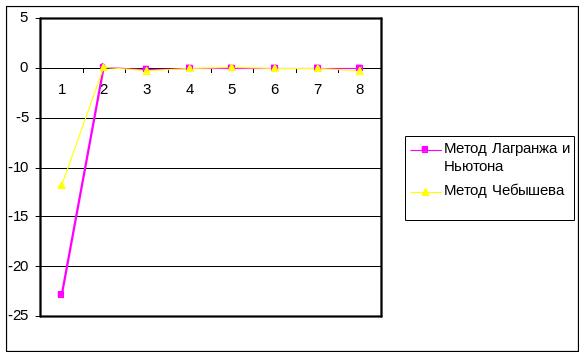
Рисунок 4. График зависимости R(x)=f(n) для точки

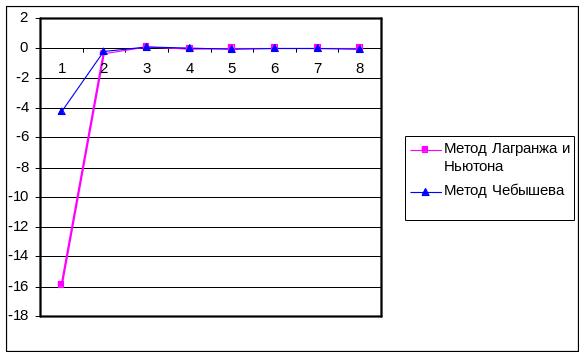
Рисунок 5. График зависимости R(x)=f(n) для точки