1.3 Физические процессы в вакууме

Вязкость газов

При перемещении твердого тела со скоростью vп за счет переда­чи количества движения молекулам газа возникает сила внутреннего трения.

В области низкого вакуума газ между подвижной 2 и неподвижной 1 пластинами можно разделить на слои толщиной L, где L – средняя длина свободного пути, рис. 1.4.

Рис. 1.4.

Скорость движения каждого слоя различна и линейно зависит от расстояния между поверхностями переноса. В плоскости х₀ происходят столкновения молекул, вылетевших из плоскостей х^` и х^``.

Причиной возникновения силы вязкостного трения является то, что движущиеся как единое целое отдельные слои газа имеют различную скорость, вследствие чего происходит перенос количества движения из одного слоя в другой. Изменение количества движения в результа­те одного столкновения равно 2mLdv_п/dx. В среднем в отрицательном и положительном направлениях оси х в единицу времени единицу пло­щади в плоскости х₀ пересекают согласно (1.8) nv_ap/4 молекул, тогда общее изменение количества движения в единицу времени для плоскости х₀

(1.28)

Сила трения по всей поверхности переноса, согласно второму закону Ньютона, определяется общим изменением количества движения в единицу времени:

, (1.29)

где А - площадь поверхности переноса; η - коэффициент динамической

вязкости газа:

. (1.30)

Отношение η/ρ называют коэффициентом кинематической вязкости. Согласно полученному выражению коэффициент динамической вязкости при низком вакууме не зависит от давления.

С повышением температуры газа η изменяется по зависимости

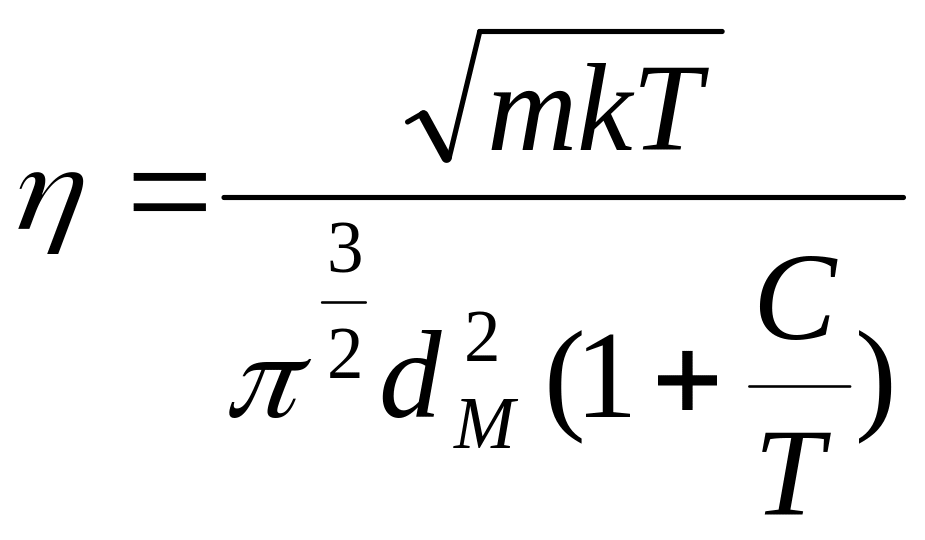. (1.31)

В области высокого вакуума молекулы газа перемещаются между движущейся поверхностью и неподвижной стенкой без соударения. В этом случае сила трения рассчитывается по уравнению

Fтр = -mv_пv_apA/4_. (1.32)

Сила трения в области высокого вакуума пропорциональна моле­кулярной концентрации или давлению газа. Уравнение (1.32) с учетом (1.13) можно записать

. (1.33)

откуда следует, что сила трения возрастает пропорционально корню квадратному из абсолютной температуры.

В области среднего вакуума сила трения

. (1.34)

При низком вакууме L→0 и формула (1.34) совпадает с (1.29), а при высоком вакууме, когда L→∞cовпадает с (1.33).

Перенос теплоты в вакууме

Теплопередача в разреженных газах может происходить за счет конвекции, теплопроводности и излучения.

При низком вакууме конвективный теплообмен играет важную роль. Перенос теплоты конвекцией от поверхности нити, нагретой до температуры Т_н, к стенкам камеры, имеющим температуру Т, описыва­ется уравнением

Е_к = α(Т_н-Т)А, (1.35)

где α - коэффициент теплообмена; А - площадь поверхности нити. Ко­эффициент теплообмена в условиях вынужденной конвекции при попе­речном обтекании нити воздухом

α_в = Nuλ/d, (1.36)

где λ - коэффициент теплопроводности газа; d - характерный размер, диаметр нити; Nu=k₁Re^k2 - критерий Нуссельта; Re=v_гdr/h - критерий Рейнольдса; v_г - скорость газового потока; k₁ и k₂ - константы.

Теплопроводность газа в качестве явления переноса при низком вакууме можно рассматривать аналогично вязкости газа. Вместо коли­чества движения в этом случае переносится энергия молекул газа.

Количество теплоты, отнесенное к одной молекуле газа,

Q₁=c_vmT_, (1.37)

где с_v- теплоемкость газа при постоянном объеме; m - масса молеку­лы газа; Т - абсолютная температура.

Если концентрация газа n постоянна, то аналогично (1.29) по­лучим выражение для теплового потока:

, (1.38)

где λ_н - коэффициент теплопроводности газа при низком вакууме:

λ_н = nmv_арLc_v/2 = ηc_v. (1.39)

Коэффициент теплопроводности газа равен произведению коэффи­циента динамической вязкости на удельную теплоемкость, которую можно рассчитать по формуле

, (1.40)

где γ=с_p/с_v - отношение теплоемкости газа при постоянном давлении к теплоемкости при постоянном объеме (для одноатомных газов γ=1,66; для двухатомных γ=1,4; для трехатомных γ=1,3); k - посто­янная Больцмана; m - масса молекулы газа.

Теплопередачу излучением в низком вакууме можно определить по закону Стефана-Больцмана:

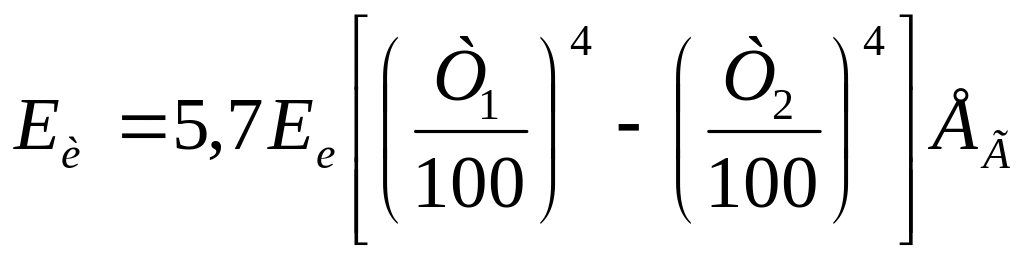, (1.41)

где Е_и - плотность теплового потока, Вт/м ; Т₁, Т₂ – температуры на внешней и внутренней поверхности переноса; Е_г – геометрический фактор (для параллельных плоскостей и цилиндрических оболочек Е_г=1); Е_е - приведенная степень черноты.

В высоком вакууме конвективным теплообменом для технических расчетов пренебрегают. Теплопроводность газа между двумя поверх­ностями с температурой Т₂ и Т₁, используя (1.8) oпишем

, (1.42)

Или с учетом уравнения газового состояния и (1.40)

E_т = - λ_b(dT/dx)A, (1.43)

где λ_b - коэффициент теплопроводности газа при высоком вакууме:

, (1.44)

т.е. при высоком вакууме коэффициент теплопроводности пропорциона­лен давлению.

Теплопередачу излучением в высоком вакууме рассчитываем по формуле (1.41).

В области среднего вакуума конвективный теплообмен рассчиты­ваем по формулам (1.35), (1.36). А коэффициент теплопроводности приближенно

, (1.45)

где g₁ и g₂ примерно равны длине свободного пути L при средней

температуре.

Электрические явления в вакууме

Прохождение электрического тока через газы при приложении разности потенциалов связано с перемещением электронов и положи­тельных ионов. При отсутствии электрического поля энергетическое распределение электронов, ионов и нейтральных молекул одинаково.

Среднюю длину свободного пути электронов в вакууме определим по формуле

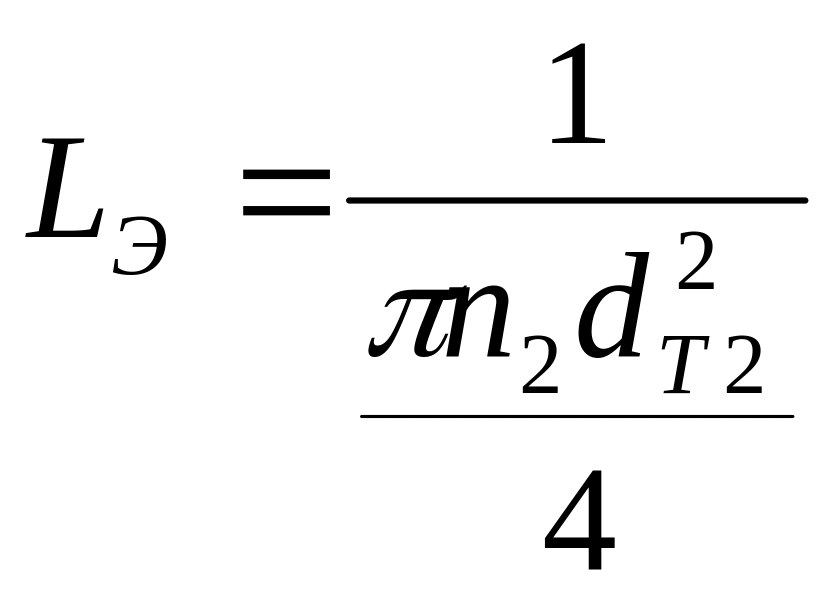, (1.46)

где n₂ - концентрация молекул газа; d_T2 - эффективный диаметр мо­лекулы газа; L_э - средняя длина свободного пути электронов.

Длина свободного пути электронов не зависит от их концентра­ции и при одинаковой концентрации молекул в 5,6 раза больше, чем у положительных ионов.

Ионизация молекул остаточных газов с образованием свободных электронов и положительных ионов возможна при воздействии на моле­кулу α-, β-, или γ-излучения с энергией, превышающей энергию ионизации соответствующего газа. Наиболее часто для ионизации применя­ют электронную бомбардировку. Минимальна энергия ионизации у гелия и неона, максимальна - у метана.

Электропроводность газового промежутка при самостоятельном разряде (без дополнительных ионизирующих излучений) зависит от давления. Электропроводность газа при низком вакууме мала, в об­ласти среднего вакуума наблюдаются наибольшие значения электропро­водности, при высоком вакууме, в связи с малым количеством частиц_, электропроводность газа еще меньше, чем при низком.

Прохождение тока через газы в области среднего вакуума сопро­вождается свечением газа в зависимости от рода и давления газа.

Диффузия в газах

В низком вакууме уравнение стационарной диффузии молекул газа имеет следующий вид:

, (1.47)

где D - коэффициент диффузии; dn/dx - градиент концентрации; Рп -

плотность потока частиц в направлении, противоположном градиенту

концентрации.

Коэффициент самодиффузии в низком вакууме согласно (1.6), (1.13), (1.47)

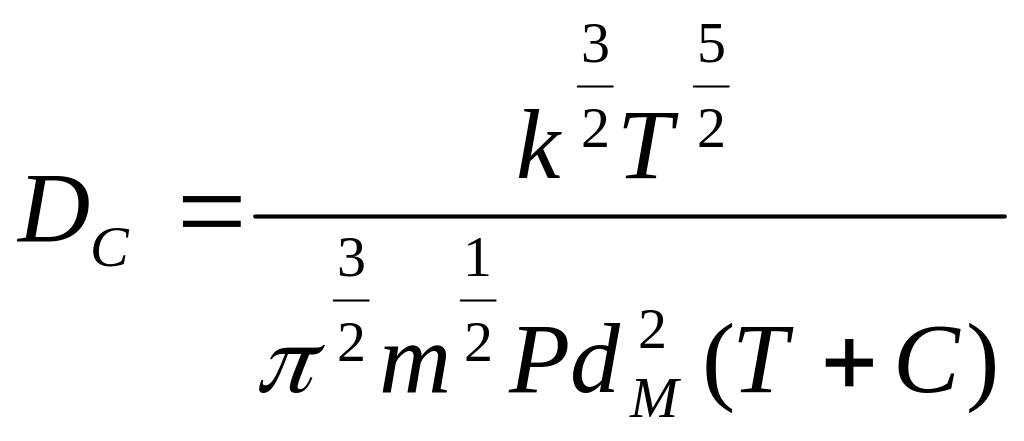. (1.48)

Таким образом, коэффициент самодиффузии в области низкого ва­куума обратно пропорционален давлению. Температурная зависимость коэффициента самодиффузии определяется множителем Т^5/2(Т+С).

Коэффициент взаимной диффузии D_в двух газов при низком вакуу­ме

, (1.49)

где d₁ и d₂ - эффективные диаметры молекул газа с массой m₁ и m₂.

Коэффициент взаимной диффузии Dв не зависит от процентного состава смеси и обратно пропорционален общему давлению.

В области высокого вакуума при разности концентраций (n₁-n₂) скорость диффузии

. (1.50)

В области среднего вакуума скорость диффузии можно рассчитать по приближенному уравнению

P_n=D_c(n₁-n₂)/d, (1.51)

где d - расстояние между поверхностями переноса;

.

Режимы течения газов

Уравнение стационарной диффузии газа в элементе вакуумной системы в соответствии с (1.47) и учетом массы молекулы газа m, площади проходного сечения А и длины элемента l можно записать

, (1.52)

где P - поток газа через трубу, измеряемый массой газа, проходящей

через элемент в единицу времени, кг/с; n₁, n₂ - концентрации моле­кул газа на концах элемента; D_э - коэффициент диффузии.

Преобразуем (1.52) с учетом (1.6):

. (1.53)

Если газовый поток выразить не в кг/с а в условных единицах потока газа, то согласно (1.53) и (1.7)

Q = U(P₁-P₂), (1.54)

где U - проводимость элемента вакуумной системы, зависящая от сте­пени вакуума, при котором происходит течение газа. В низком вакуу­ме проводимость растет при повышении давления, в высоком она оста­ется постоянной. В низком вакууме при высоких давлениях возможно существование инерционного режима течения газа, аналогичного тур­булентному режиму, рассматриваемому в гидродинамике. Силы инерции движущейся массы газа, вызывающие образование вихрей, приводят к сложному характеру распределения скорости движения газа по попе­речному сечению элемента.

Для определения условия существования инерционного режима те­чения можно пользоваться критерием Рейнольдса Re=dv_г/υ, где d - характерный размер элемента; v_г - скорость течения газа; υ - коэффициент кинематической вязкости. При Re>2200 возникает инерционный режим течения газа.

При течении газов в трубопроводах условие существования инер­ционного режима можно записать в другой форме, выразив vг через поток газа Q:

.

Для воздуха при комнатной температуре Re>2200 при Q>3000d, где Q - поток газа, м³Па/с; d - диаметр тру­бопровода, м.

В элементах вакуумных систем такие потоки встречаются в ос­новном в момент запуска, т.е. режим этот нехарактерен для вакуум­ных систем.

В низком вакууме основную роль играет вязкостный режим тече­ния газа, при котором характер распределения скорости в поперечном сечении определяется силами внутреннего трения.

При высоком вакууме силы внутреннего трения в газах стремятся к нулю и существует режим течения газа, для которого характерно независимое перемещение отдельных молекул. Это молекулярный режим.

В среднем вакууме существует переходный - молекулярно-вяз­костный режим.

Отверстием называется трубопровод, длина которого значительно меньше диаметра. Примем, что отверстие расположено в стенке, раз­деляющей два бесконечно больших объема. Давление воздуха в одном объеме Р₁, в другом Р₂. Площадь отверстия А. Тогда, в зависимости от отношения давлений r=Р₂/Р₁, при комнатной температуре проводи­мость отверстия:

при 1> r > 0,528 U_ов=289(0,72 - 0,68r⁶)A/(1-r); (1.55)

при 0,528> r >0,1 U_ов=200A/(1-r); (1.56)

при r < 0,1 U_ов=200A. (1.57)

Проводимость отверстия в условиях высокого вакуума при моле­кулярном режиме

, (1.58)

где М - в кг/моль; Т - в К; U - в м³/с. Для воздуха при комнатнойтемпературе U=116А.

Для среднего вакуума при молекулярно-вязкостном режиме тече­ния проводимость

U_омв = U_омb+U_ов, (1.59)

где

.

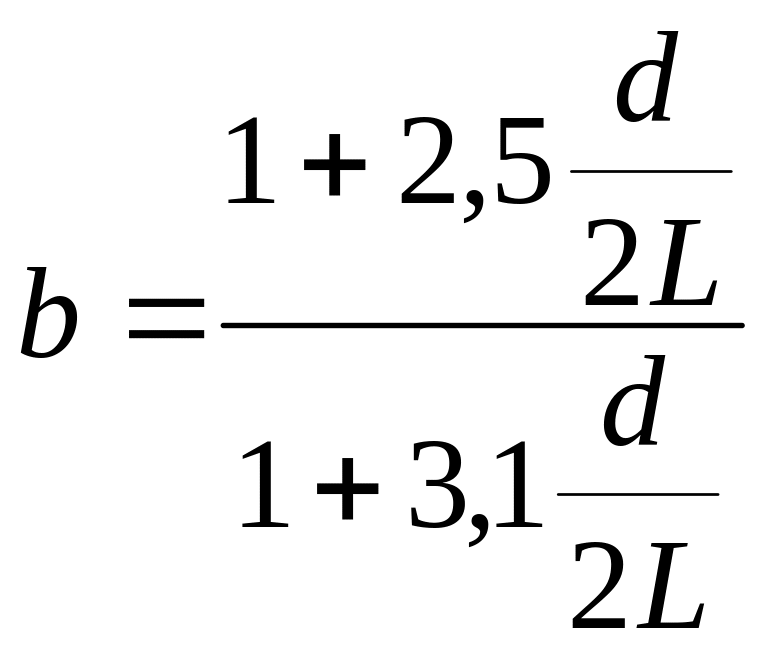Проводимость трубопровода при вязкостном режиме течения

U_тв = 1360d⁴(P1+P2)/(2l), (1.60)

где d - диаметр; l - длина трубопровода.

Проводимость трубопровода постоянного сечения при молекуляр­ном режиме течения газа в условиях высокого вакуума

U_тм = 4v_apА²/(3Вl), (1.61)

где А - площадь поперечного сечения трубопровода, В - его периметр

Для воздуха при т=293 К проводимость цилиндрического трубопровода длиной l и диаметром d U_тм = 121d³/l.

В области среднего вакуума можно пользоваться для приближен­ных расчетов формулой

U_тмв = 0,9U_тм + U_тв. (1.62)