Лекции по вакуумной технике.

1. Физика вакуума

1.1 Понятие о вакууме и давлении

Основой физики вакуума являются следующие постулаты:

1) Газ состоит из отдельно движущихся молекул.

2) Существует постоянное распределение молекул газа по скоростям.

3) При движении молекул газа нет преимущественного движения.

4) Температура газа - величина, пропорциональная его средней кине­тической энергии молекул.

5) При взаимодействии с поверхностью твердого тела молекулы газа адсорбируются.

В а к у у м - состояние газа при более низком давлении, чем атмосферное. При давлениях, близких к атмосферному, пользуются ко­личественным определением вакуума как разности атмосферного и абсолютного давлений. При абсолютном давлении, отличающемся от ат­мосферного более чем на два порядка, эта разность остается практи­чески постоянной и не может служить количественной характеристикой разреженного газа. В этих условиях вакуум определяют абсолютным давлением газа. При очень малых давлениях, которые не могут быть измерены приборами, состояние газа можно характеризовать количест­вом молекул в единице объема - молекулярной концентрацией газа.

Согласно второму закону Ньютона, давление молекулы на поверх­ность твердого тела:

, (1.1)

где ΔA - площадь поверхности; Δt - время взаимодействия молекулы

с поверхностью.

Давление газа на поверхность твердого тела найдем интегриро­ванием по объему полусферы, из которой молекулы достигают поверх­ности за время Dt, с радиусом R=vDt. С учетом выражения (1.1)

(1.2)

Вводя вместо постоянной среднеквадратичную скорость, получим

, (1.3.)

где n - молекулярная концентрация.

Учитывая, что плотность газа ρ=nm, выражение (1.3) можно при­вести к виду

Р = ρv_кв/3.

Уравнение (1.3) применимо при условиях равновесия, т.е. ра­венства потоков падающих и вылетающих молекул газа. Равенство мо­жет нарушаться, например, при адсорбции молекул на поверхности.

Атмосферный воздух - основная газовая смесь, с которой прихо­дится иметь дело в вакуумной технике. Он состоит в основном из азота, кислорода, паров воды и др. При 25ºС и 50% влажности парци­альное давление паров воды - 12 гПа (табл. 1.1).

В качестве нормальных условий приняты давление 10⁵ Па и тем­пература 273 К. При этом объем, занимаемый 1 кмоль, равен 22,4 м³.

Таблица 1.1

Состав сухого атмосферного воздуха.

Газы	Содержание, %	Парциальное давление, гПа	Газы	Содержание, %	Парциальное давление, гПа
N2 O2 Ar CO2 Ne He	78,1 21 0,9 0,03 0,0018 0,00052	781 210 9 0,3 0,018 0,0052	CH4 Kr N2O H2 Xe	0,0002 0,0001 0,00005 0,00005 0,000009	0,002 0,001 0,0005 0,0005 0,00009

Газовые законы

Парциальное давление газа - давление, оказываемое химически индивидуальным газом, содержащимся в газо­вой смеси, равное давлению, какое бы оказывал этот газ, если бы он был без других примесей при тех же условиях.

Если в объеме находится смесь из К химически не взаимо­действующих газов, то для определения давления смеси Рсм необходи­мо подсчитать сумму

(1.4)

Сравнивая (1.3) и (1.4), можно записать

(1.5.)

Последнее выражение - закон Дальтона: общее давление смеси химически не взаимодействующих газов равно сумме парциальных дав­лений смеси.

Учитывая, что температура пропорциональна средней кинети­ческой энергии молекул газа, можно записать mV_кв/2=сТ, где с - по­стоянная. Тогда уравнение (1.3) для расчета давления газа можно представить в виде P=2ncT/3. Если обозначить k=2c/3, то

Р = nkT, (1.6)

а средняя кинетическая энергия молекул

mV_кв/2 = 3kT/2.

Уравнение (1.6) - уравнение газового состояния, связывающее между собой три основных параметра состояния газа: давление, моле­кулярную концентрацию и температуру. Постоянная k - постоянная Больцмана, ее экспериментальное значение 1,38·10^-23 Дж/К.

Уравнение (1.6) можно записать

(1.7)

где М - молекулярная масса газа; V - объем газа; R - универсальная

газовая постоянная: R=kN =8,31·10³ Дж/(К·моль); N - число Авогад­ро: N =М/m=6,02·10²⁶ кмоль^-1.

Следствия из (1.7):

1. Закон Гей-Люссака - при постоянной массе и неизменном давлении объем газа пропорционален его абсолютной температуре.

2. Закон Шарля - при постоянной массе газа и его объеме давление газа пропорционально его абсолютной температуре.

3. Закон Бойля-Мариотта - при постоянных массе и температуре газа произведение его давления на объем неизменно.

4. Закон Авогадро - при постоянном давлении и температуре газа мо­лекулярная концентрация не зависит от рода газа.

Частота соударений газа с поверхностью

Число молекул, ударяющихся о единицу поверхности в единицу времени, или частота соударений,

N_q=nV_ар/4, (1.8)

где Vар - среднеарифметическая скорость молекул газа.

Объем газа, ударяющийся о единицу поверхности в единицу вре­мени, можно выразить через частоту соударений и молекулярную кон­центрацию:

V_q=N_q/n=V_ар/4. (1.9)

Полученное выражение не зависит от давления и определяет максимальную быстроту действия идеального вакуумного насоса, отка­чивающего все молекулы газа, которые попадают в него через входное отверстие.

Давление атмосферного воздуха зависит от высоты над уровнем моря и определяется по формуле Больцмана

(1.10)

где Р_о - давление газа у поверхности земли, z - высота.

Согласно формуле Больцмана, при подъеме на каждые 15 км давление воздуха уменьшается примерно на один порядок.

Распределение молекул по скоростям

При соударениях друг с другом или стенками вакуумной камеры молекулы газа изменяют свои скорости как по величине, так и по направлению. Скорость, при которой наблюдается максимум функции распределения, называется наиболее вероятной скоростью:

(1.11)

Обозначив с=v/v_вер, можно записать функцию распределения мо­лекул по скоростям так:

(1.12)

Безразмерные функции распределения

и

показаны на графике, рис. 1.1.

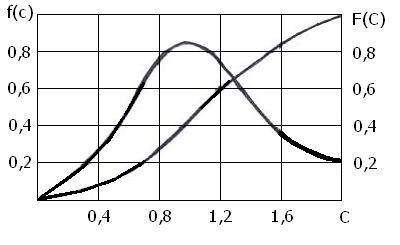
Рис. 1.1.

Функция F(c) численно равна доле общего числа молекул, скорости которых не превышают с.

В вакуумных расчетах часто используют скорости: среднеарифметическую

; (1.13)

среднеквадратичную

(1.14)

Соотношение между скоростями v_вер, v_ар, v_кв равно 1:1,128: 1,225. Так, для азота при 0ºС v_вер=402 м/с, v_ар=453 м/с, v_кв=492 м/с.

Средняя длина свободного пути

Направленный молекулярный поток, содержащий в начальный мо­мент N молекул газа, за счет столкновений с хаотически движущимися молекулами с частотой К за время dt уменьшается на величину

dN=-KNdt. После интегрирования получим

N = N_oe^-Kt = N_oe^-l/L. (1.15)

Средняя длина свободного пути молекул газа определяется отно­шением скорости молекул к числу столкновений в единицу времени: L=v/K.

Столкновение молекул произойдет, если расстояние между цент­рами молекул не более диаметра молекулы d_m. Примем, что одна молекула имеет радиус d_m, а остальные - математические точки с нулевым радиусом. При движении со скоростью v в газе с молекулярной кон­центрацией n такая молекула опишет объем и испытает cоударений. Средняя длина пути в этом случае

(1.16)

С учетом относительных скоростей движения молекул газа, кото­рые не учитывались, получим более точное выражение:

(1.17)

Опытные данные показывают, что при постоянной молекулярной концентрации с увеличением температуры длина свободного пути уве­личивается. Это можно учесть введением дополнительного множителя, определяемого экспериментально:

(1.18)

где С - постоянная Сазерленда, равная температуре, при которой в случае постоянной молекулярной концентрации газа средняя длина свободного пути молекул уменьшается вдвое по сравнению со значени­ем, соответствующим бесконечно большой температуре (табл.1.2).

С учетом взаимодействия молекул газа между собой (взаимного притяжения) и учетом (1.6) формулу (1.18) можно записать:

(1.19)

Для воздуха при Т=293 К и давлении 1 Па из (1.19) следует, что L₁ = 6,7·10^-3 м·Па. При любом другом давлении

L = L₁/P=6,7·10^-3/P, (1.20)

где Р - в Па; L - в м.

Таблица 1.2

Средняя длина свободного пути молекул различных газов при давлении 1 Па

Газы	L1·103, м·Па при t,К				Газы	L1 ·103, м·Па при t, K
	600	293	77	4,2		600	293	77	4,2
N2 O2 Ar CO2 Ne Kr	20,8 16,9 16,7 11,6 30,7 14,1	8,67 7,02 6,79 4,32 13,9 5,52	1,26 1,00 0,933 0,492 2,50 0,691	0,0061 0,0047 0,0042 0,0019 0,0165 0,0029	H2 Xe H2O Воздух He	28,2 10,5 13,9 16,0 43,6	12,2 3,93 4,38 6,72 19,1	0,197 0,448 0,391 0,995 3,13	0,0108 0,0017 0,0013 0,0048 0,0174

Понятие о степенях вакуума

Многие физические процессы в вакууме существенно зависят от соот­ношения между числом взаимных столкновений молекул и числом столк­новений молекул со стенками вакуумной камеры. Частота столкновений между молекулами Кm обратно пропорциональна средней длине свобод­ного пути: К_m=v_ap/L. Среднее число соударений со стенкой камеры , где F - площадь поверхности стенок, сопри­касающихся с разреженным газом; V - объем камеры; d_эф=4V/F - эф­фективный размер вакуумной камеры.

Для молекул газа внутри сферического сосуда диаметром D d_эф=2D/3, для трубы бесконечной длины с диаметром D d_эф=D, а для двух бесконечных параллельных поверхностей, расположенных на расстоянии D друг от друга, d_эф=2D.

Отношение К_с/К_m - критерий Кнудсена

Kn = K_c/K_m = L/d_эф (1.21)

В зависимости от значения этого критерия различают вакуум низкий, средний и высокий.

Низкий вакуум - состояние газа, при котором взаимные столкно­вения между молекулами преобладают над столкновениями молекул газа со стенками вакуумной камеры, Kn<<1. При этом длина свободного пу­ти молекул газа значительно меньше размеров вакуумной камеры. При напылении в низком вакууме столкновения молекул газа с молекулами распыленного вещества не дают возможности получить на стенках камеры изображение экрана, поставленного на пути молекулярного пучка. Из условия изменения режима течения газа принимают Kn<0,005.

Средний вакуум - состояние газа, когда частоты соударений мо­лекул друг с другом и со стенками камеры одинаковы: L=d_эф, Kn=1.

Высокий вакуум - состояние газа, при котором столкновения мо­лекул газа со стенками камеры преобладают над взаимными: Kn>1. В этом случае, при напылении, изображение экрана на пути молекуляр­ного пучка получается отчетливым. Из условия изменения режима те­чения газа принимают Kn>1,5. Тогда условие существования среднего вакуума можно записать в виде 0,005<Kn<1,5.