Министерство образования Российской Федерации
Камский Государственный Политехнический Институт
ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МОДЕЛИ и МЕТОДЫ
Линейное программирование
Учебное пособие для студентов экономических специальностей
Набережные Челны
2004
Учебное пособие по экономико-математическим моделям и методам разработано на кафедре «Математическое моделирование и информационные технологии в экономике» и предназначено для студентов экономических специальностей. Оно включает в себя теоретический материал, примеры моделирования реальных экономических задач и их методы решения. Приведенные алгоритмы решения задач ориентированы на использование современных информационных технологий.
Для организации самостоятельной работы приводятся варианты индивидуальных заданий с примерами их решения.
Составители: Смирнов Ю.Н., Шибанова Е.В.
Набережные Челны: Изд-во КамПИ, 2004, 81 с.
Рецензент: доцент, кандидат физико-математических наук Углов А.Н.
Печатается по решению научно-методического совета Камского государственного политехнического института от 24.03.03 г.
Камский Государственный
Политехнический Институт,
2004
Содержание
Содержание 3
1. Введение 4
2. Примеры задач линейного программирования 5
3. Общая, стандартная и основная задачи линейного программирования 8
4. Геометрическая интерпретация задачи линейного программирования 11
5. Графический метод решения задачи линейного программирования 13
6. Симплекс - метод решения задач линейного программирования 16
7. Двойственные задачи линейного программирования 33
8. Двойственный симплекс-метод 42
9. Задача целочисленного линейного программирования 46
10. Транспортная задача 52
11. Задачи производственного менеджмента 69
Задание для самостоятельной работы 73
Варианты задач для самостоятельной работы 74
Литература 80
Введение
Линейное программирование является одним из разделов математического программирования – дисциплины, занимающей изучением экстремальных задач и разработкой методов их решения.
В
общем виде постановка экстремальной
задачи математического программирования
состоит в определении наибольшего или
наименьшего значения функции
,
называемой целевой функцией, при условиях
,
где f
и
-
заданные функции, а
- заданные постоянные величины. При этом
ограничения в виде равенств определяют
множество допустимых решений, а
- называются проектными параметрами.
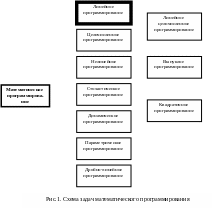
В зависимости от свойств функции f и задачи математического программирования делятся на ряд классов задач. Далеко неполная схема задач математического программирования приведена на рис.1.
Среди
них наиболее изученными являются задачи
линейного
программирования
(ЛП), когда все функции
f
и
- линейные.
Нелинейное программирование – если хотя бы одна из функций f и - нелинейная.
Выпуклое программирование – если отыскивается минимум выпуклой (максимум вогнутой) функции, заданной на выпуклом замкнутом множестве.
Целочисленное программирование – если проектные параметры могут принимать лишь целочисленные значения.
Дробно-линейное программирование – если целевая функция f – квадратичная, - линейные.
Параметрическое программирование – если функции f и зависят от некоторых параметров.
Стохастическое программирование – если в функциях f и содержаться случайные величины.
Динамическое программирование – если процесс нахождения решения является многоэтапным.
Рассмотрим задачи, сводящиеся к задачам линейного программирования.
