13

Лабораторна робота № 3

Тема: Робота з командами арифметичних операцій

Мета:

- ознайомлення з системами числення та переведення чисел з однієї системи в іншу;

- застосування арифметичних операцій над двійковими числами для написання програм ;

-застосування арифметичних операцій на десятковими (ВСD) числами для написання програм ;

Теоретичні відомості.

1. Системи числення

Системою числення називається сукупність правил запису чисел. Системи числення підрозділяються на позиційні і непозиційні. Як позиційні, так і непозиційні системи числення використовують визначений набір символів — цифр, послідовне сполучення яких утворить число. Непозиційні системи числення характеризуються тим, що в них символи, що позначають те чи інше число, не змінюють свого значення в залежності від місця розташування в записі цього числа.

Класичним прикладом такої системи числення є римська. У ній для запису чисел використовуються букви латинського алфавіту. При цьому буква I означає одиницю, V — п'ять, Х — десять, L — п'ятдесят, С — сто, D — п'ятсот, М — тисячу. Для одержання кількісного еквівалента числа в римській системі числення необхідно просто додати кількісні еквіваленти вхідних у нього цифр. Виключення з цього правила складає випадок, коли молодша цифра йде перед старшою, — у цьому випадку потрібно не складати, а віднімати число входжень цієї молодшої цифри. Приміром, кількісний еквівалент числа 577 у римській системі числення — це DLXXVII = 500 + 50 + 10 + 10 + 5 + 1 + 1 = 577. Інший приклад: CDXXIX = 500 -100+10+10 - 1 + 10 ⁼ 429.

У позиційній системі числення кількість символів у наборі дорівнює основі системи числення. Місце кожної цифри в числі називається позицією. Номер позиції символу (за винятком одиниці) у числі називається розрядом. Розряд 0 називається молодшим розрядом. Кожній цифрі відповідає визначений кількісний еквівалент.

У загальному випадку кількісний еквівалент деякого додатнього числа А в позиційній системі числення можна представити виразом:

,

де: р — основа системи числення (деяке ціле додатнє число);

а — цифра даної системи числення; п — номер старшого розряду числа. Для одержання кількісного еквівалента числа в деякій позиційній системі числення необхідно скласти добуток кількісних значень цифр на степені основи, показники яких дорівнюють номерам розрядів.

Двійкова система числення

Набір цифр для двійкової системи числення:{0, 1}, основа степені р = 2.

Кількісний еквівалент деякого цілого n-значного двійкового числа обчислюється відповідно до формули :

Наявність цієї системи числення обумовлено тим, що комп'ютер побудований на логічних схемах, що мають у своєму елементарному виді тільки два стани - включений і виключений

Наприклад, розглянемо двійкове число 10100111.

Обчислимо кількісний еквівалент цього двійкового числа це буде величина, рівна наступній сумі:

1 2⁷ + 0 2⁶ + 1 2⁵ +0 2⁴ + 0 2³ + 1 2² + 1 2¹ + 1 2⁰=167

Додавання і віднімання двійкових чисел виконується так само, як і для інших позиційних систем числення, наприклад десяткової. Точно так само виконуються позика і перенос одиниці з (в) старший розряд.

Наприклад:

11 11111 перенесення

110011011 +

110010101

1100110000

Шістнадцятерична система числення

Дана система числення має наступний набір цифр:

{0, 1, 2, .... 9, А, В, С, D, Е, F}, основа системи р = 16.

Кількісний еквівалент деякого цілого n-значного шітнадцятеричного числа обчислюється відповідно до формули:

Наприклад, кількісний еквівалент 16-кового числа f45ed23c дорівнює:

15 16⁷+4 16⁶+5 16⁵+ 14*16⁴+13 16³+2 16²+3 16¹+12 16⁰

Таблиця

Десяткове число	Двійкова тетрада	Шістнадцятеричне число
0	0000	0
1	0001	1
2	0010	2
3	0011	3
4	0100	4
5	0101	5
6	0110	6
7	0111	7
8	1000	8
9	1001	9
10	1010	А,а
11	1011	B,b
12	1100	С, с
13	1101	D,d
14	1110	Е,е
15	1111	F,f
16	10000	10

Таблиця містить представлення десяткових чисел з діапазону 0-16 у двійковій і шістнадцятеричній системах числення. Таблицю зручно використовувати для взаємного перетворення чисел. Шістнадцятерична система числення при проведені обчислень трохи складніша, ніж двійкова, зокрема, у тому, що стосується правил переносів у старші розряди. Головне тут — пам'ятати наступну рівність:

(1+F=10)₁₆

Ці переходи дуже важливі при виконанні додавання і вирахування шістнадцятеричних чисел.

Десяткова система числення

Дана система числення має наступний набір цифр:

{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, основа ступеня р = 10.

Кількісний еквівалент деякого цілого n-значного десяткового числа обчислюється відповідно до формули:

Переведення чисел з однієї системи числення в іншу

Переведення у десяткову систему числення

Цей тип переводу найбільш простий. Звичайно його роблять за допомогою алгоритму заміщення, суть якого полягає в наступному: спочатку в десяткову систему числення переводиться основа степені р, а потім — цифри вихідного числа. Результати підставляються у формулу:

Отримана сума і буде шуканим результатом.

Переведення у двійкову систему числення

Переведення з десяткової системи числення

1. Розділити десяткове число А на 2. Запам'ятати частку q і залишок а.

2. Якщо в результаті кроку 1 частка q  0, то прийняти її за нове ділене і відзначити залишок а, що буде черговою значущою цифрою числа, повернутися до кроку 1, на якому в я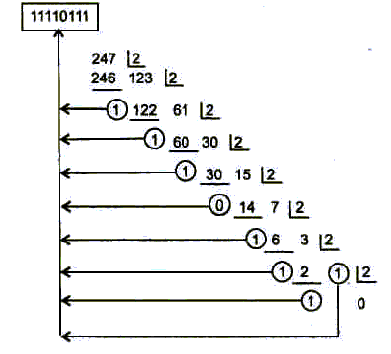 кості діленого (десяткового числа) бере участь отримане на кроці 2 частка.

3. Якщо в результаті кроку 1 частка q= 0, алгоритм припиняється. Виписати залишки в порядку, зворотному їхньому одержанню. Вийде двійковий еквівалент вихідного числа.

Наприклад, потрібно перевести число 247 у двійкову систему числення

Порядок обходу залишків для одержання результату показано стрілками, і результат перетворення дорівнює 11110111.

Переведення з шістнадцяткової системи числення

Суть його полягає в послідовній заміні шістнадцятеричних цифр відповідними двійковими тетрадами згідно вище наведеної таблиці. Наприклад e4d5-> 1110 0100 1101 0101.

Переведення у шістнадцятеричну систему числення

Переведення з десяткової системи числення

Загальна ідея такого переведення аналогічна переведенню в двійкову систему числення з десяткової.

1. Розділити десяткове число А на 16. Запам'ятати частка q і залишок а.

2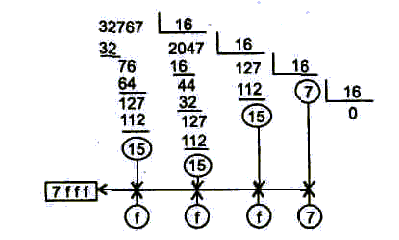 . Якщо в результаті кроку 1 частка q  0, то прийняти його за нове ділене, записати залишок і повернутися до кроку 1.

3. Якщо частка q = 0, припинити роботу алгоритму. Виписати залишки в порядку, зворотному їхньому одержанню. Вийде шістнадцятеричний еквівалент вихідного десяткового числа.

Наприклад, потрібно перевести 32 767 у шістняцятеричну систему числення

Порядок обходу залишків для одержання результату показаний на стрілками. Результат перетворення дорівнює 7fff.

Переведення із двійкової системи числення

Алгоритм аналогічний алгоритму переведення з двійкової системи числення в шістнадцаятеричну. Двійкове число розбивається на тетради, починаючи з молодшого розряду. Далі кожна тетрада приводиться до відповідного шістнадцятеричного числа.

Наприклад, перевести число 11100101101011110101100011011000111101010101101 у шістнадцятеричну систему числення.

Розіб'ємо його на тетради:

0111 0010 1101 0111 1010 1100 0110 1100 0111 1010 1010 1101

По тетрадам приводимо послідовності нулів і одиниць до шістнадцятеричного представлення: 72D7AC6C7AAD.

Переведення дробових чисел

Особливо це важливо при програмуванні алгоритмів, що використовують операції з плаваючою крапкою . Для цього використовується формула:

Розглянемо операції перекладу чисел на прикладах.

Приклад

Перевести в десяткове представлення дріб у двійковій системі числення 110100,01001011.

Для переведення використовується формула:

110100,01001011=1*2⁵ +1*2⁴ +0*2³ +1*2² +0*2¹ +0*2⁰ +0*2^-1+1*2^-2+0*2^-3 +0*2^-4 +1*2^-5 +0*2^-6 +1*2^-7 +1*2^-8.

Обчислити цілу частину десяткового дробу 1*2⁵ +1*2⁴ +0*2³ +1*2² +0*2¹+0*2⁰. Для обчислення дробової частини 0*2^-1+1*2^-2+0*2^-3 +0*2^-4 +1*2^-5 +0*2^-6 +1*2^-7 +1*2^-8 виразу використовують таблицю.

Таблиця