1 Способ
Алгоритм решения. В качестве первого делителя взять 2, присвоить это значение некоторой переменной i;
начать цикл "пока i <= n";
если данное число n делится на i, тогда выдать на экран значение i и разделив данное число на i, присвоить новое значение той же переменной n (n := n div i);
далее цикл продолжить, но значение i не увеличивать на 1, а проверить деление нового значения n на прежнее значение i;
если n не делится на i, тогда i увеличить на 1 (i := i + 1) и продолжить цикл, т.е. выполнить проверку условия цикла (i <= n), а затем снова проверить деление n на уже новое значение i.
Program Problem3; { Разлож. числа на прост. множит.. 1- й спос. }
uses Crt;
var
n, i : integer;
begin
write('Введите натуральное число '); readln(n);
write('Простые делители числа ', n, ' следующие; ');
i := 2;
while i <= n do
if n mod i =0 then
begin
write(i, ' ');
n := n div i
end
else i := i + 1
end.
2 Способ.
Алгоритм решения.
Вначале находим все делители, равные 2. Для этого последовательно делим число 360 на 2:
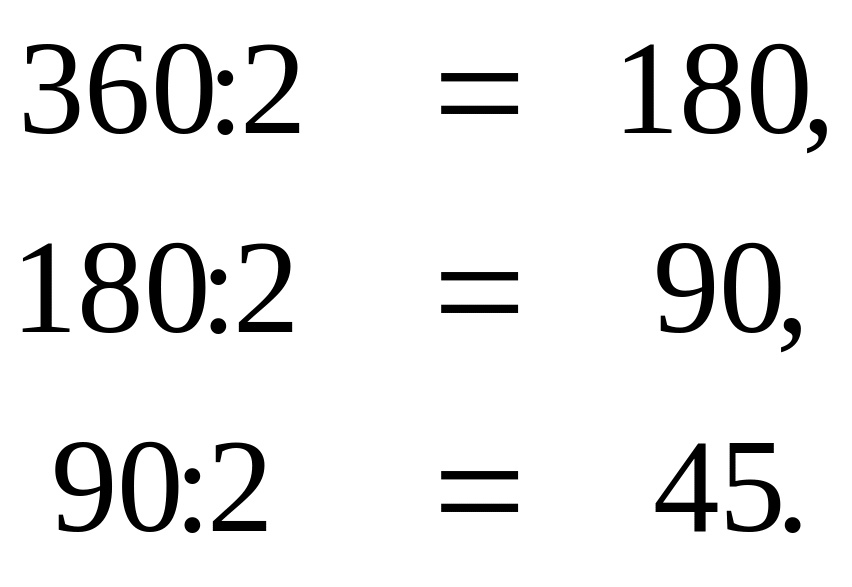
После этого, полученный результат делим на нечетные числа. Причем на каждое нечетное число делим не один раз, а до тех пор, пока такое деление будет возможным.
Делим на 3: 45:3 = 15, 15:3 = 5.
Делим на 5: 5:5 = 1.
Делим на 7, не делится, пробуем делить на следующее нечетное число.
Делим на 9, не делится, переходим к следующему нечетному числу.
Делим на 11, не делится, и так далее.
До тех пор будем пробовать деление на нечетные числа, пока они будут меньше или равны получаемому частному от деления числа на соответствующий делитель.
На основании этих соображений составляем программу.
Program Problem3a;
uses Crt;
var
i, n : integer;
begin
write('Введите целое число '); readln(n); writeln;
writeln('Простые делители целого числа ', n);
{----------------------------------------------------------------------------------------}
while n mod 2 = 0 do { Цикл для вывода делителей, равных 2 }
begin
write(2, ' ');
n := n div 2
end;
{----------------------------------------------------------------------------------------}
i := 3;
while i <= n do { Цикл для нечетных делителей }
if n mod i = 0
then
begin
write(i, ' ');
n := n div i
end
else i := i + 2;
writeln
end.
Задача 4. Написать программу, в результате выполнения которой выяснится, входит ли цифра 2 в запись данного целого числа n.
Решение
Алгоритм решения.
1. Начало. Переменные целого типа n, p, k: n - для вводимого числа; p - для цифр этого числа; k - счетчик, подсчитывающий количество цифр в числе, равных 2.
2. Ввод целого числа.
Счетчику k устанавливается первоначальное значение 0.
3. Цикл, пока n <> 0. В цикле, переменной p присваивать значение цифры числа.
Если p = 2, тогда увеличивать k на единицу.
Вычесть из числа n последнюю цифру и разделить его на 10.
Продолжить и закончить цикл.
4. Если k = 0, тогда выдать сообщение: "Цифра 2 не входит в запись числа", иначе, выдать сообщение: "Цифра 2 входит в запись числа".
5. Конец.
Program Problem4; { Входит ли цифра 2 в запись числа }
uses WinCrt;
var
n, p, k : integer;
begin
write('Введите целое число '); readln(n);
k := 0;
while n <> 0 do
begin
p := n mod 10;
if p = 2 then k := k + 1;
n := n div 10
end;
if k = 0 then writeln('Цифра 2 не входит в запись этого числа')
else writeln('Цифра 2 входит в запись этого числа')
end.
Задача 5. Составить программу вывода всех натуральных чисел, меньших n, квадрат суммы цифр которых равен заданному числу m.
Решение
Алгоритм решения.
1. Раздел описаний.
Переменные: n, m, k, a, p, s. Тип целый.
n - для границы значений натуральных чисел, m - для числа, с которым сравнивается квадрат суммы цифр (точный квадрат), k - для натуральных чисел от 1 до n, a - для запоминания натурального числа, перед тем, как будет определяться сумма его цифр, p - для цифр числа, s - для суммы цифр.
2. Раздел операторов.
Ввод значений n и m. Установить первоначальное значение для k (эта переменная "перебирает" все натуральные числа от 1 до n, k := 1).
Цикл, пока k <= n.
В цикле: установить первоначальные значения для суммы s (s:=0); запомнить число в переменную a (a := k).
Цикл для подсчета суммы цифр, пока k <> 0.
В цикле: выделять по одной цифре числа, известным способом; прибавлять по одной цифре к сумме; уменьшать число на последнюю цифру и на порядок.
Закончить цикл для подсчета суммы цифр.
Проверка выполнения условия.
Если квадрат суммы цифр равен заданному числу,
тогда вывести это натуральное число на экран.
Перейти к проверке следующего числа.
Закончить основной цикл проверки чисел.
3. Закончить программу.
Program Problem5;
uses Crt;
var
n, m, k, a, p, s : integer;
begin
write('Введите натуральное число, до которого ');
write('выводить искомые числа '); readln(n);
writeln('Введите число, с которым сравниваете квадрат');
write('его суммы цифр. Оно должно быть точн. квадрат. '); readln(m);
write('Искомые числа: ');
k := 1;
while k <= n do
begin
s := 0; a := k;
while k <> 0 do
begin
p := k mod 10;
s := s + p;
k := k div 10
end;
if sqr(s) = m then write(a, ' ');
k := a + 1
end
end.
Задача 6. Найти наименьшее натуральное число, дающее при делении на 2, 3, 4, 5, 6 соответственно остатки 1, 2, 3, 4, 5.
Решение
Алгоритм решения. Берется наименьшее натуральное число - единица и находятся остатки от деления его на 2, 3, 4, 5 и 6; если остатки будут равны 1, 2, 3, 4 и 5, тогда это число является искомым, его надо выдать на экран и закончить программу, в противном случае, надо брать следующее натуральное число - 2 и проверять его, и так далее.
Program Problem6;
uses WinCrt;
var
n : integer;
begin
n := 0;
repeat
n := n + 1;
until (n mod 2 = 1) and (n mod 3 = 2) and (n mod 4 = 3) and
(n mod 5 = 4) and (n mod 6 = 5);
writeln('Искомое целое число ', n)
end.
Задача 7. Числа, одинаково читающиеся и слева направо, и справа налево, называются палиндромами. Например, числа 42324 или 1331 - палиндромы. Составьте программу, которая будет находить числа - палиндромы из заданного промежутка
Решение
Алгоритм решения. Переставить цифры в числе и сравнить полученное число с заданным.
Пусть заданное число a, тогда введем еще одну переменную b, которой будет присвоено значение переменной a (для чего это делается вы узнаете позже): b := a;
Заведем еще одну переменную a1 для нового числа, в котором цифры уже будут переставлены.
Первоначальное значение этой переменной - ноль: a1 := 0;
Почему значение этой переменной равно нулю станет ясно из программы.
Далее организуем цикл repeat, в котором будет происходить перестановка цифр числа b:
repeat
a1 := a1*10 + b mod 10;
b := b div 10
until b = 0;
Итак, в цикле, также как и в цикле while ... do ..., отделяется последняя цифра:
b mod 10; (например, 343 mod 10 = 3); переменной a1 присваивается значение:
a1 := a1*10 + b mod 10; 0 * 10 + 3 =3;
"отбрасывается" последняя цифра заданного числа с помощью операции целочисленного деления:
b := b div 10; 343 div 10 = 34;
проверяется условие: b = 0, 34 = 0, условие не выполняется, значит цикл продолжается.
Отделяется последняя цифра уже нового числа:
b mod 10 = 34 mod 10;
новое число a1, уже равное 3, умножается на 10 и к результату прибавляется следующая цифра - 4:
a1 := a1*10 + b mod 10;
"отбрасывается" последняя цифра числа b:
b := b div 10 ; 34 div 10 = 3;
проверяется условие: b = 0, 3 = 0; условие не выполняется, значит цикл продолжается.
Отделяется последняя цифра числа:
b mod 10 ; 3 mod 10 = 3;
формируется новое число:
a1 := a1*10 + b mod 10 ; 34 * 10 + 3 = 343;
"отбрасывается" последняя цифра числа и получается новое число:
b := b div 10 ; 3 div 10 = 0;
проверяется условие: b = 0, 0 = 0; условие выполняется, значит цикл заканчивается.
Теперь становится ясно, почему введена другая переменная b для заданного числа, ее значение в цикле меняется от начального до нуля и, чтобы сохранить заданное число в переменной a, и вводится, так сказать, "рабочая" переменная - b.
После окончания цикла перестановки цифр числа, сравнивается первоначальное число, которое "сохранилось" в переменной a и число, которое получилось после перестановки цифр и "накопилось" в переменной a1.
Если a = a1, тогда значение a выдается на экран, так как это число является палиндромом.
Далее, значение a увеличивается на 1, т. е. берется для рассмотрения следующее по порядку натуральное число и снова продолжается внешний цикл. Цифры числа переставляются, полученное новое число после перестановки цифр - a1, сравнивается с первоначальным a и так далее.
Внешний цикл заканчивается, когда значение a становится равным правой границе интервала - n.
Program Problem7;
uses Crt;
var
m, n, a, b, a1 : longint;
begin
write('Введите левую границу промежутка '); readln(m);
write('Введите правую границу промежутка '); readln(n);
a := m;
writeln('Числа палиндромы из [', m, ';', n, ']');
repeat
b := a; a1 := 0;
repeat
a1 := a1*10 + b mod 10;
b := b div 10
until b=0;
if a1 = a then write(a, ' ');
a := a + 1
until a > n;
end.
Задача 8. Программа, подсчитывающая сумму цифр числа.
Решение
Program Sum; { Сумма цифр числа }
uses Crt;
var
n, s, a : integer;
begin
write('Введите целое число '); readln(n);
a := n; s := 0;
repeat
s := s + n mod 10; n := n div 10
until n = 0;
writeln('Сумма цифр числа ', a, ' равна ', s)
end.
Задача 9. Программа перестановки первой и последней цифр в числе:
Решение
Program Transpose;
uses Crt;
var
n, n1, p, a, i : longint;
begin
write('Введите натуральное число n '); readln(n);
a := n; i := 1;
p := n mod 10; {последняя цифра введенного числа}
repeat
i := i*10; n := n div 10
until n<10;
n1 := a - n*i - p + n + p*i;
writeln('Число после перестановки цифр ', n1)
end.
Задача 10. Если мы сложим все цифры какого-либо числа, затем - все цифры найденной суммы и будем повторять это много раз, мы наконец получим однозначное число (цифру), называемое цифровым корнем данного числа. Например, цифровой корень числа 561 равен 3 (5 + 6 + 1 = 12; 1 + 2 = 3). Составьте программу для нахождения числового корня числа.
Решение
Program Problem10; { Цифровой корень числа }
uses Crt;
var
n, a, s : integer;
begin
write('Введите натуральное число '); readln(n);
a := n;
repeat
s := 0;
while n <> 0 do
begin
s := s + n mod 10; n := n div 10
end;
n := s
until n < 10;
writeln('Цифровой корень числа ', a, ' равен ', n)
end.
Задача 11. Составить программу определения всех делителей числа n.
Решение