1.4.Матричная форма представления основных законов электротехники.

С использованием матриц инциденций М и N, а также матриц режимных параметров можно представить в компактной матричной форме основные законы электротехники.

1.4.1.Закон Ома

Матричное уравнение:

U_B = Z_BI - E_B (1.1)

Структура матриц:

= . -

U_B – матрица падений напряжений в ветвях схемы;

I – вектор токов в ветвях;

E_B – матрица ЭДС в ветвях;

Z _B – матрица сопротивлений в ветвях, где Z_ij, i = j – взаимные сопротивления ветвей обусловленных взаимной индуктивностью ветвей;

Z_ij = Z_ji = 0 – в установившемся симметричном режиме функционирования электрической системы.

Пример 1.2

Записать в матричной форме закон Ома для расчетной схемы:

Z₁ = 0,1 Е₁ = 100

Z₂ = 0,3 Е₃ = 200

Z₃ = 0,5

= . -

1.4.2.Первый закон Кирхгофа

Матричная форма записи позволяет представить баланс токов для всех узлов схемы одновременно.

M · I = J

Структура матриц:

1 ветви m

. =

M – матрица инциденций первого рода;

I – вектор неизвестных токов в ветвях;

J – вектор задающих токов.

Если J_i < 0, то он моделирует подключение нагрузки, если J_i > 0, то он моделирует генерацию мощности в i-том узле.

Пример 1.3

Записать первый закон Кирхгофа в матричной форме и перейти к системе уравнений:

Узлы нагрузочные:

J₁ = -5

J₂ = -3

J₃ = -1

1 2 3 4 5

М =

Б -1 0 -1 -1 0 - проверка

Матричная форма:

. =

Система уравнений:

I ₃ – I₅ = -5

I₂ + I₄ + I₅ = -3

I₁ – I₂ = -1

1.4.3.Второй закон Кирхгофа

Матричная форма позволяет записать баланс напряжений для всех независимых контуров схемы:

N · U_B = 0

Структура матриц:

1 ветви m

. = 0

Преобразуем закон Кирхгофа, используя матричную запись закона Ома:

N (Z_BI - E_B ) = 0

N Z_BI = N E_B

Произведение N E_B = E_К

где Е_в = - матрица ЭДС ветвей

Е_к = - матрица ЭДС контуров

Тогда второй закон Кирхгофа имеет вид:

N Z_BI = Е_К

Структура матриц:

1 . . . . m

. . =

Z_B - диагональная матрица сопротивлений ветвей;

I – вектор неизвестных токов в ветвях.

Пример 1.4

Записать в матричной форме и в виде системы алгебраических уравнений второй закон Кирхгофа для расчетной схемы:

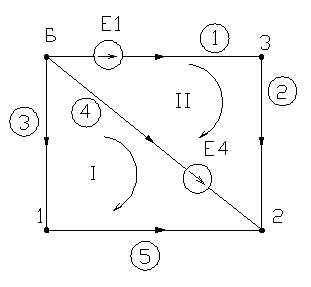
Z₁ = 0,1 Е₁ = 100

Z₂ = 0,3 Е₃ = 300

Z₃ = 0,4

Z₄ = 0,8

Z₃ = 0,6

1 2 3 4 5

N =

Найдем вектор контурных ЭДС

Е_К = N· Е_В

Е_К = . = =

В матричной форме:

. . =

. =

N Z_B · I = Е_К

Система уравнений:

- 0,4 I₁ + 0,8 I₄ – 0,6 I₅ = 300

0,1 I₁ + 0,3 I₂ – 0,8 I₄ = -200

Задание 2

Используя вариант расчетной схемы и исходные данные записать 1 и 2 законы Кирхгофа в матричной форме и в виде системы уравнений .