В. Газові суміші

Газова суміш - це механічна суміш газів, не вступаючих між собою в хімічні реакції. Вона може бути задана масовими, об'ємними або молярними частками.

Масовою часткою називають відношення маси М_i кожного газу, що входить в суміш, до загальної маси М суміші:

Об'ємною часткою називають відношення приведеного об'єму V_i газу до загального об'єму суміші V_см газів:

де V_i - приведений об'єм, тобто об'єм, який займав би компонент газу при певній температурі і тиску суміші

Молярною часткою називається відношення числа молей K_i кожного газу до числа молей К- К_i /К суміші. Молярна частка чисельно рівна об'ємній частці:

Газова постійна суміші газів залежно від способу завдання суміші

або .

Середня (уявна) молярна маса суміші

або

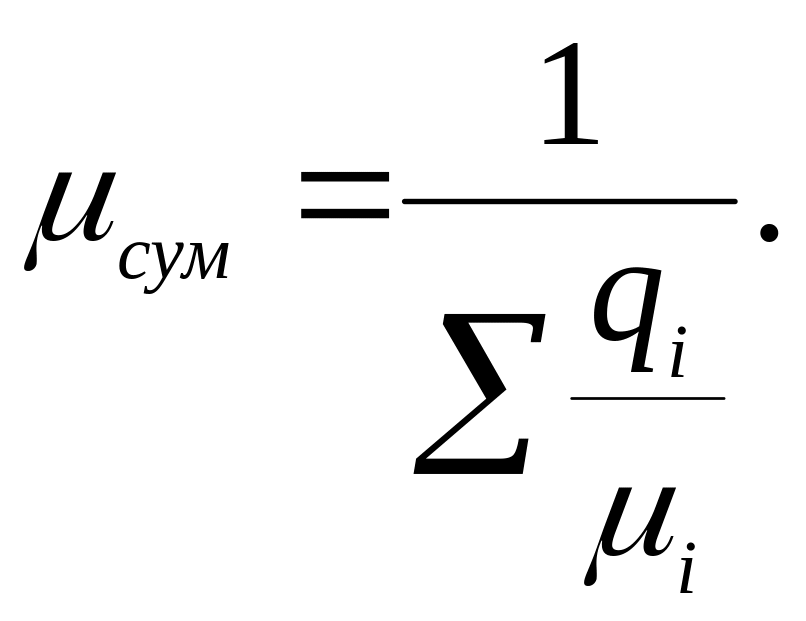
Парціальний тиск кожного газу дорівнює добутку загального тиску суміші на його об'ємну частку:

Параметри газової суміші можуть бути обчислені з рівняння Клапейрона PV=MRT, де всі величини, що входять в рівняння, відносяться до суміші газів.

Приклад 4. Об'ємний склад сухих продуктів згоряння палива наступний, %: Знайти уявну молярну масу, газову постійну, густину і питомий об'єм продуктів згоряння при В=750 мм рт.ст., t=800°С.

Рішення

Г. Термодинамічні процеси ідеального газу

Термодинамічним процесом називають зміну параметрів стану робочого тіла. Існує нескінченна кількість термодинамічних процесів, їх називають політропними, і зміна параметрів в них підкоряється рівнянню: PVⁿ = const, де n - показник політропи.

Окремими процесами є ізохорний (V=const), ізобарний (P=const), ізотермічний (T=const) і адіабатний (dq=const), який протікає без відведення і підведення теплоти. Для будь-якого процесу зміна внутрішньої енергії 1 кг газу обчислюється за виразом:

при С_v = const DU = C_v (t₂ – t₁).

зміна ентальпії при С_v = const Dt = C_p (t₂ – t₁).

зміна ентропії :

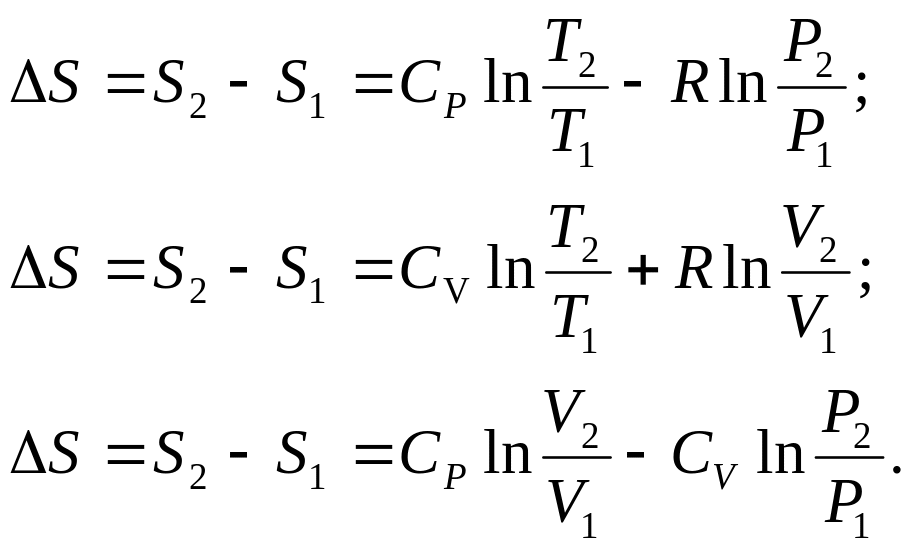
Приклад 5. В закритій посудині знаходиться повітря при тиску Р₁=5 бар і температурі t₁=27⁰ С. Визначте тиск повітря після охолодження до 0°С. Зобразите процес в P-V і Т-S - координатах.

Рішення. Залежність між початковими і кінцевими параметрами в ізохорному процесі . Тоді

Приклад 6. Визначте роботу ізобарного розширення азоту масою 7 кг при нагріванні в інтервалі температур від t₁= 200⁰С до t₂= 600⁰С. Покажіть процес в P-V-і Т-S - діаграмах.

Рішення. Робота розширення

де М - маса газу, R - газова постійна, Дж/ (кг⁰С); t₁, t₂ - відповідно початкова і кінцева температура азоту, ⁰С.

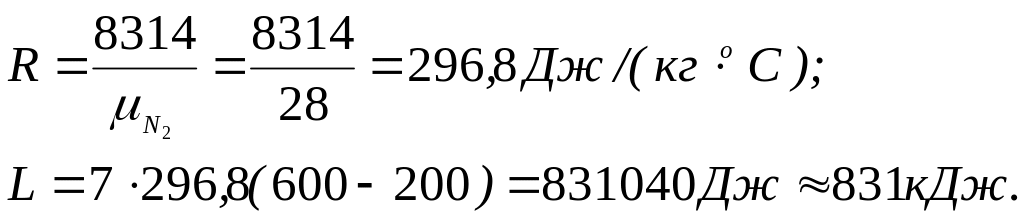
Приклад 7. 0,2 кг кисню при температурі t₁=25⁰С розширюється ізотермічно до триразового збільшення об'єму. Визначте кількість теплоти, що надається тілу.

Рішення. Оскільки в ізотермічному процесі вся підведена теплота йде на здійснення роботи, то

де Q - підведена теплота, Дж; М - маса газу, кг; R - газова постійна, Дж/(кг·К );

Т – температура газу, К; V₁ і V₂ - відповідно початковий і кінцевий об'єм, м³.

Приклад 8. Газ СО при тиску Р₁=0,9 бар і початковій температурі t₁=12⁰С адіабатно стискається до тиску Р₂=3,6 бара. Визначте температуру в кінці стиснення.

Рішення. Кінцеву температуру визначають із співвідношення параметрів Р і Т в адіабатному процесі:

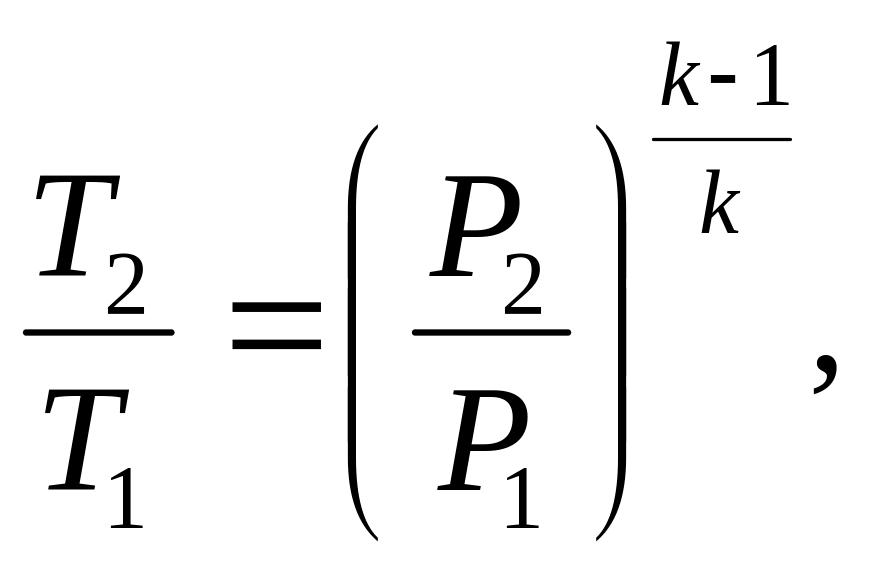
де k – показник адіабати. Для двоатомного газу k=1,4. Тоді

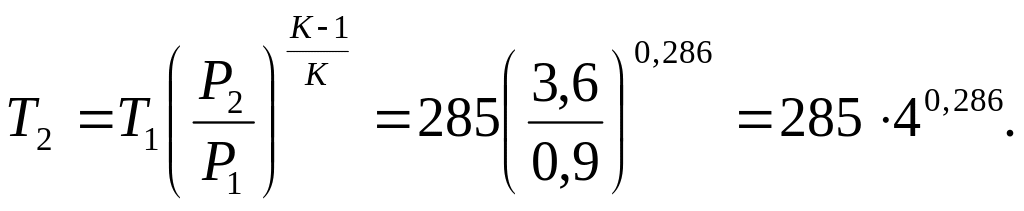
Позначимо через N. lg N = 0,286ln4 = 0,286·0,602 = 0,172.

Звідси N=1,49. Отже T₂=285·1,49=425K.