Розділ 3. Кореляційний аналіз в spss

Розв’яжемо сформульовану у розділі 2 задачу, використовуючи програму SPSS.

Після відкриття програми необхідно записати дані. Цю дію виконуємо в листі Data View, який активізований програмою автоматично. Змінні розміщуються у клітинках горизонтального ряду (var), а їх значення записуються вертикально. На рис.3.1 дана дія виконана для нашого прикладу. VAR00001, VAR00002, VAR00003 – це назви змінних, тобто x, y, k відповідно.

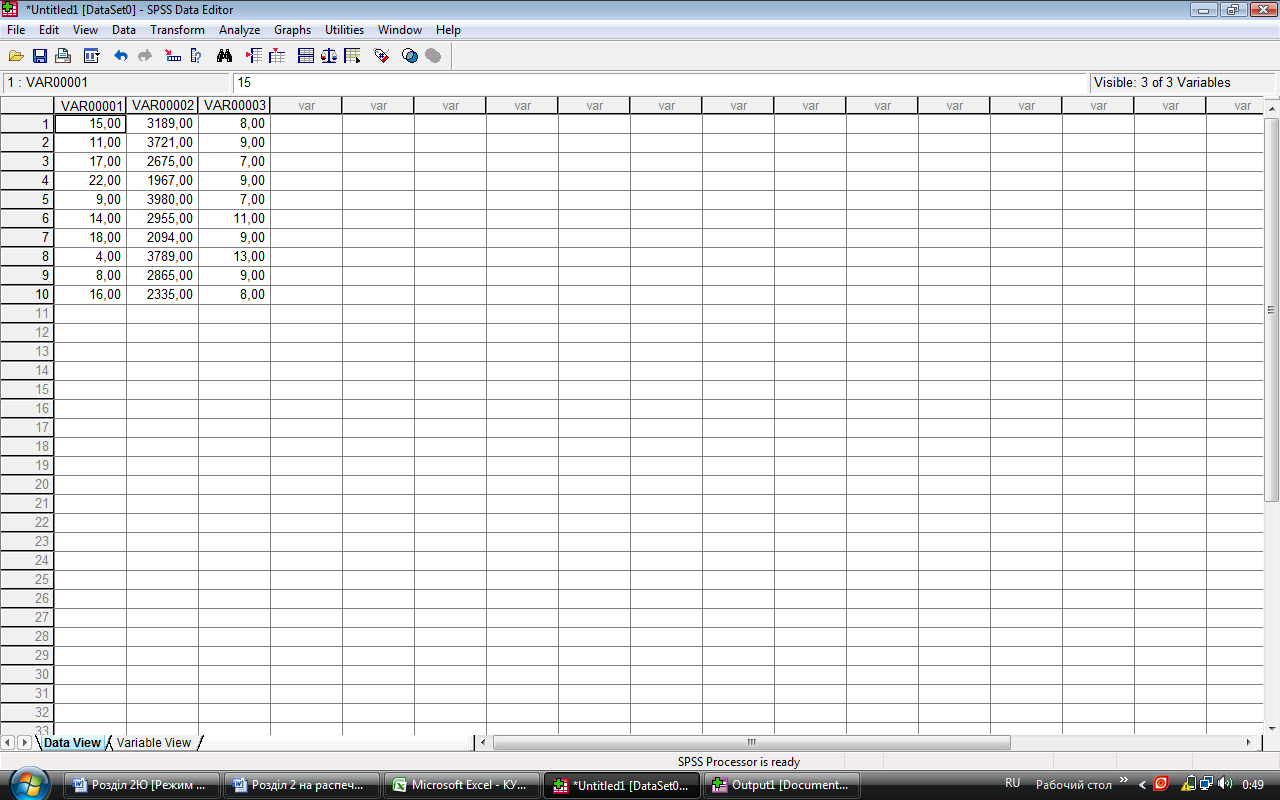
Рис. 3.1 Лист Data View.

У закладці Variable View нічого писати не потрібно, після введення даних програма автоматично заповнює відомості про змінні. Це зображено на рис.3.2.

Наступний крок – обчислення парної кореляції для змінних. Для цього на панелі інструментів натискаємо кнопку Analyze, з меню вибираємо команду Correlate, а потім – Bivariate. Відкриється наступне діалогове вікно – рис.3.3.

У лівому верхньому вікні програма автоматично записує всі початкові змінні. Для того, щоб програма обчислила парний коефіцієнт кореляції, необхідно виділити мінімум дві змінні і перенести їх у праве верхнє вікно Variables.

Рис. 3.2 Заповнення відомостей про змінні

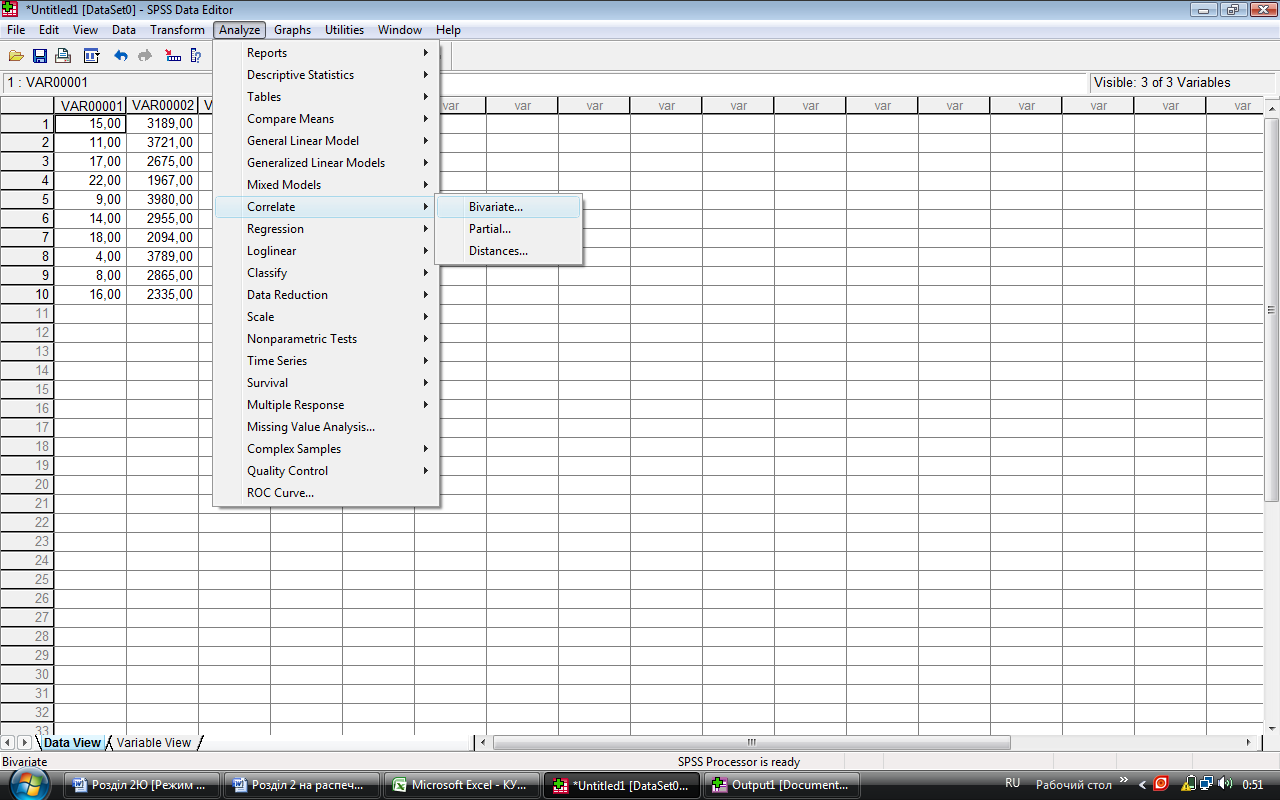
Рис. 3.3. Діалогове вікно для парної кореляції

Оскільки нам необхідно обчислити усі парні коефіцієнти, то перенесемо усі змінні у вікно Variables (рис.3.4).

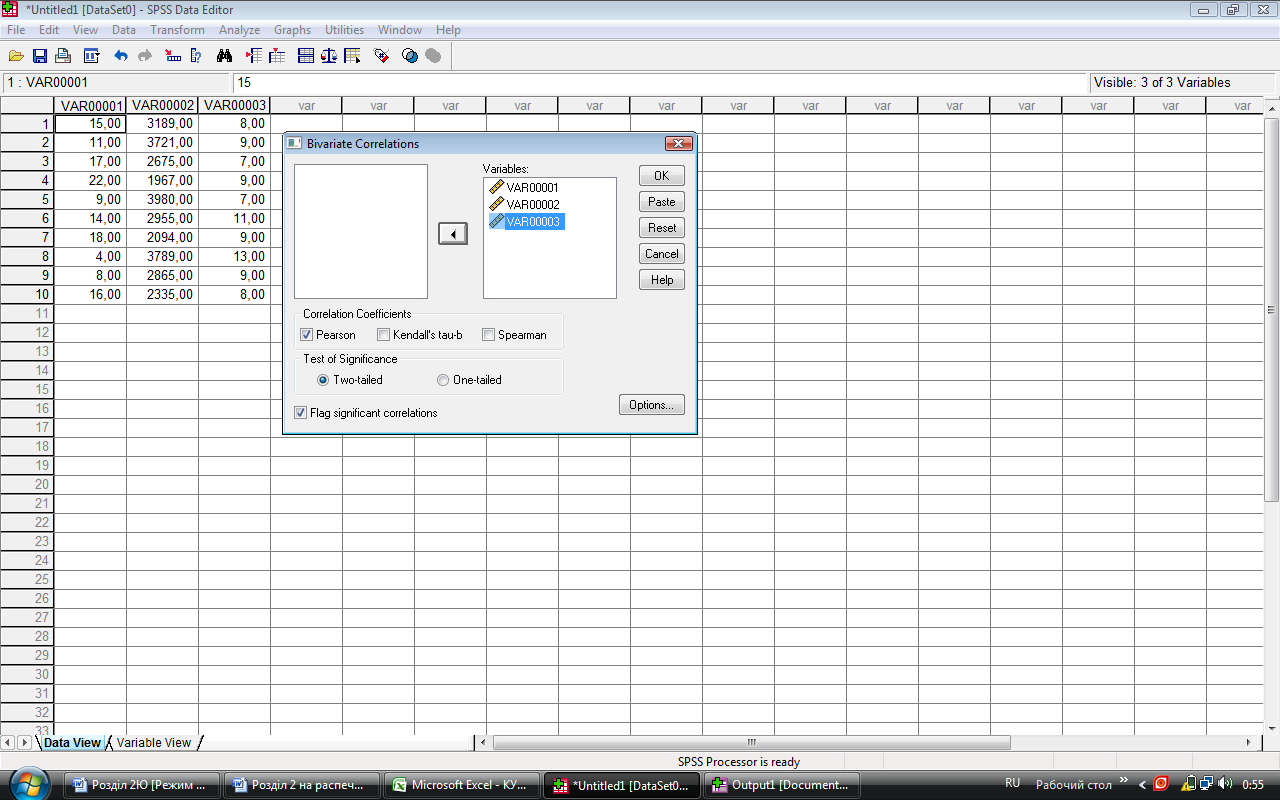Рис. 3.4. Вибір змінних для обчислення парного коефіцієнта кореляції

В параметрах Correlation Coefficients. Необхідно вибрати коефіцієнт Пірсона (Pearson) – програма робить це автоматично. Далі в параметрах Test of Significance вибираємо Two-tailed. Програма обраховує коефіцієнти кореляції і відкривається наступне вікно – рис.3.5.

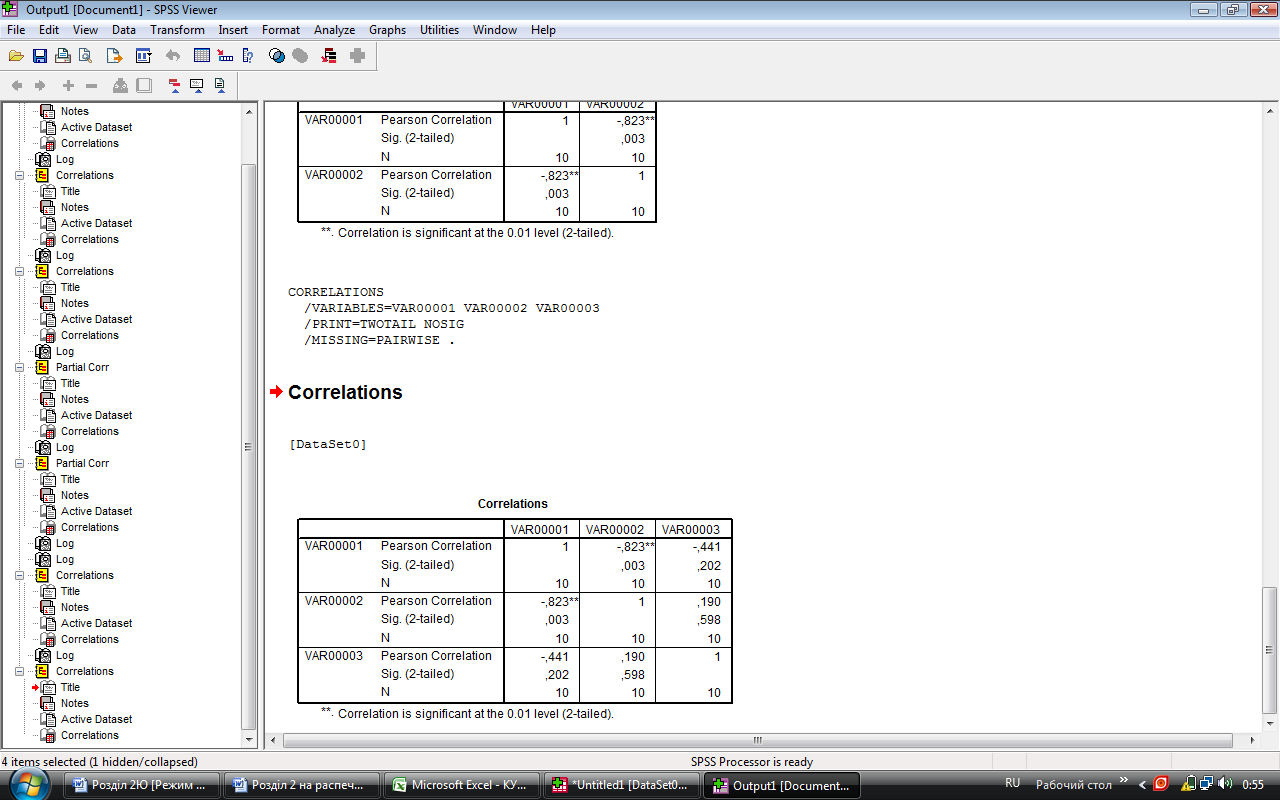
Рис. 3.5. Вивід на екран значень обчислених парних коефіцієнтів

Таким чином, обчислені парні коефіцієнти представлені у вигляді таблиці 3.1. Клітинка, що знаходиться на перетині між стовпцем і рядком з назвою змінної, і буде парним коефіцієнтом між цими змінними. Наприклад, парний коефіцієнт змінних VAR00001 і VAR00002 дорівнює 0,635, тобто r (xy) = 0,635

Таблиця 3.1

Correlations

		VAR00001	VAR00002	VAR00003
VAR 00001	Pearson Correlation	1	-,823(**)	-,441
	Sig. (2-tailed)		,003	,202
	N	10	10	10
VAR 00002	Pearson Correlation	-,823(**)	1	,190
	Sig. (2-tailed)	,003		,598
	N	10	10	10
VAR 00003	Pearson Correlation	-,441	,190	1
	Sig. (2-tailed)	,202	,598
	N	10	10	10

Для того, щоб обрахувати частинні коефіцієнти кореляції на панелі інструментів натискаємо кнопку Analyze, з меню вибираємо команду Correlate, а потім – Partial. Відкривається наступне вікно – рис.3.6.

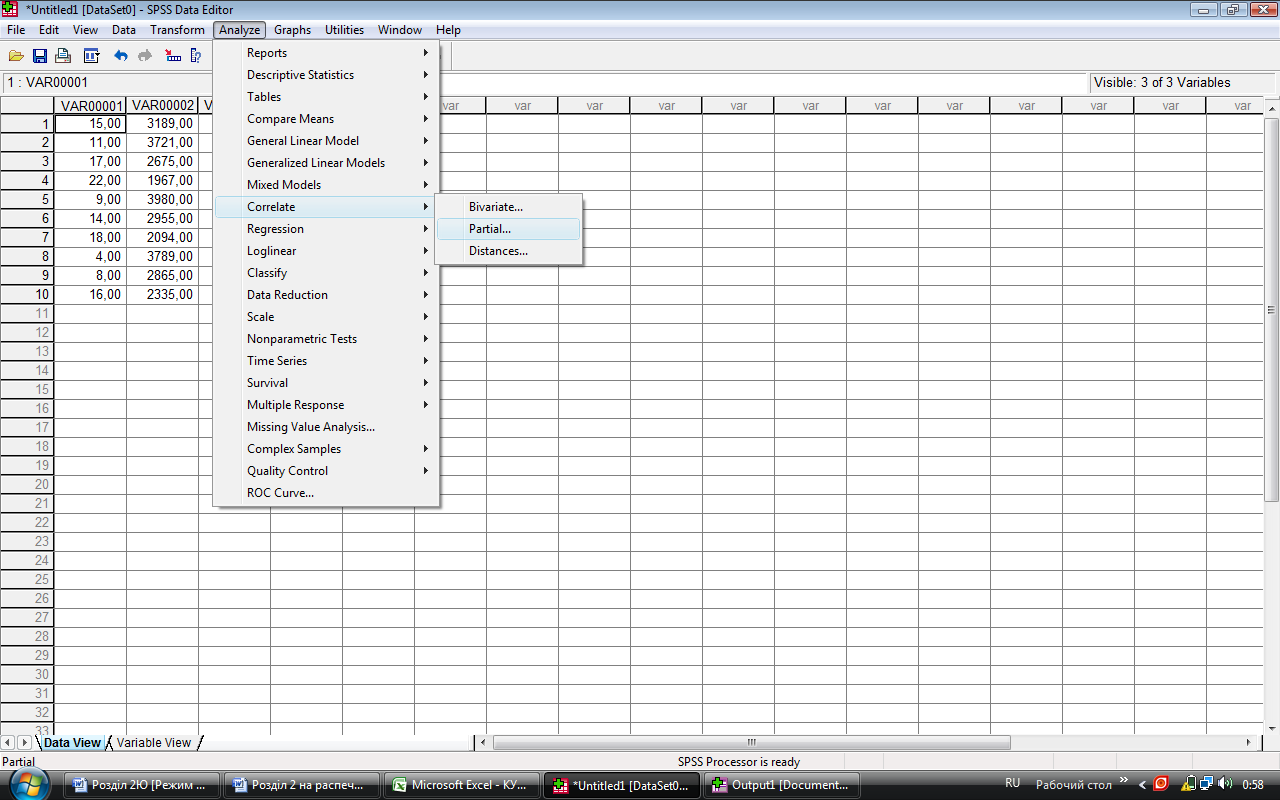Рис. 3.6. Діалогове вікно для частинної кореляції

Переносимо дві змінні з лівого вікна у праве (Variables) таким же чином, як це робили у вікні парної кореляції. А інші дві змінні (ті, вплив яких ми будемо виключати) переносимо у віконце Controlling for. Програма автоматично вибирає в вікні Test of Significance параметр Two-tailed (див. рис.3.7).

Рис. 3.7. Вибір змінних для обчислення частинного коефіцієнта кореляції

Якщо внизу вікна натиснути кнопку Options, то відкриється наступне вікно – рис.3.8.

Рис. 3.8. Опції частинної кореляції.

На екран виводяться результат обчислення – рис.3.9.

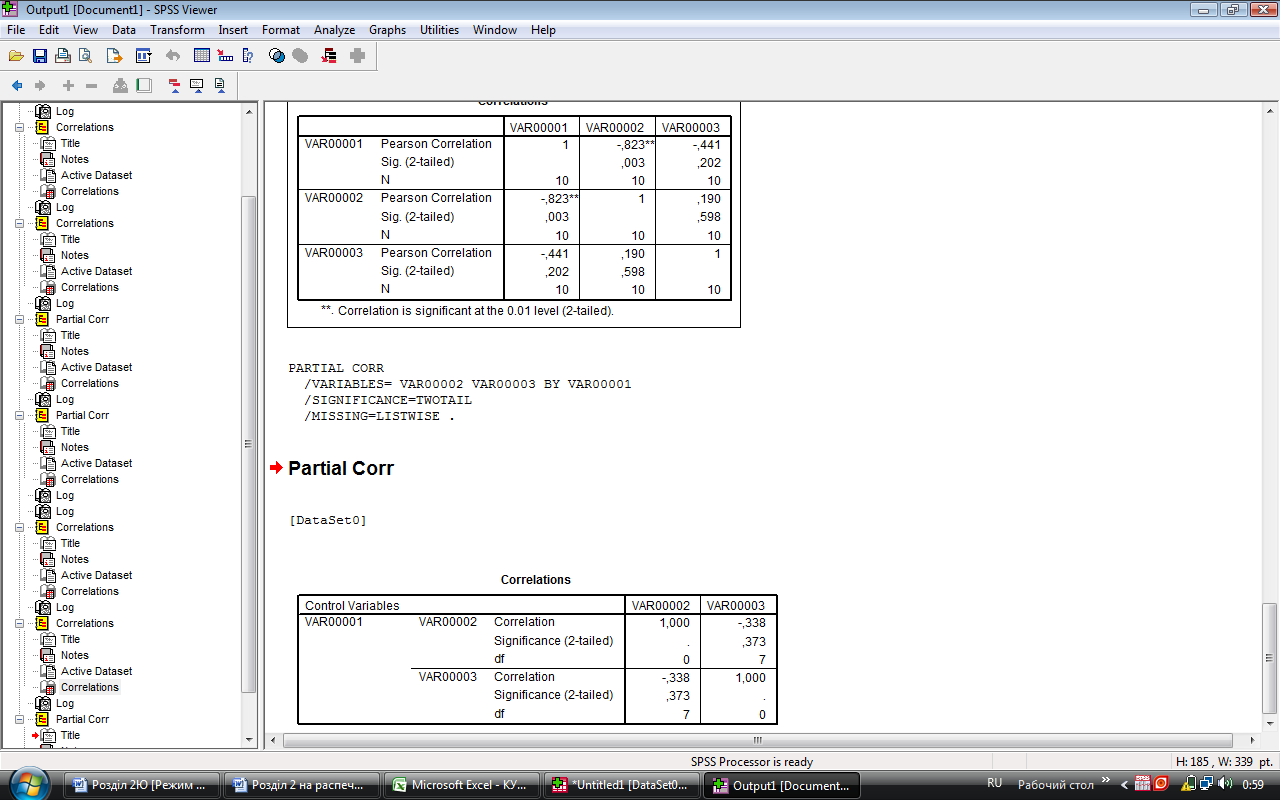
Рис. 3.9. Вивід на екран значень обчислених частинних коефіцієнтів

Результат обчислення частинного коефіцієнту кореляції між змінними VAR00001 і VAR00002, з виключенням впливу змінної VAR00003, подано в таблиці 3.2.

Таблиця 3.2

Correlations

Control Variables			VAR0001	VAR0002
VAR00003	VAR00001	Correlation	1,000	-,839
		Significance (2-tailed)	.	,005
		df	0	7
	VAR00002	Correlation	-,839	1,000
		Significance (2-tailed)	,005	.
		df	7	0

Аналогічно обраховуються частинні коефіцієнти кореляції для інших пар змінних (таблиця 3.3 та таблиця 3.4).

Результат обчислення частинного коефіцієнту кореляції між змінними VAR00002 і VAR00003, з виключенням впливу змінної VAR00001, подано в таблиці 3.3.

Таблиця 3.3

Correlations

Control Variables			VAR0002	VAR0003
VAR00001	VAR00002	Correlation	1,000	-,338
		Significance (2-tailed)	.	,373
		df	0	7
	VAR00003	Correlation	-,338	1,000
		Significance (2-tailed)	,373	.
		df	7	0

Результат обчислення частинного коефіцієнту кореляції між змінними VAR00001 і VAR00003, з виключенням впливу змінної VAR00002, подано в таблиці 3.4.

Таблиця 3.4

Correlations

Control Variables			VAR0001	VAR0003
VAR00002	VAR00001	Correlation	1,000	-,510
		Significance (2-tailed)	.	,161
		df	0	7
	VAR00003	Correlation	-,510	1,000
		Significance (2-tailed)	,161	.
		df	7	0