1.3. Частинний коефіцієнт кореляції.

Якщо змінні корелюють одна з одною, то на розмірі парного коефіцієнта кореляції частково відражається вплив інших змінних. Враховуючи це, часто з’являється необхідність дослідити часткову кореляцію між змінними при виключенні впливу однієї або декількох інших змінних.

Парний (повний) коефіцієнт кореляції між і-м і j-м випадковими змінними можуть не відповідати дійсності. Наприклад, додатня кореляція між змінними х_і і х_j можуть бути обумовленими їх залежністю від x_k, в той час коли при фіксованому x_k ці величини стохастично незалежні. Відповідно, при вивченні зв’язку між цими величинами необхідно виключати вплив x_k, тобто знайти щільність зв’язку при фіксованому значенні x_k.

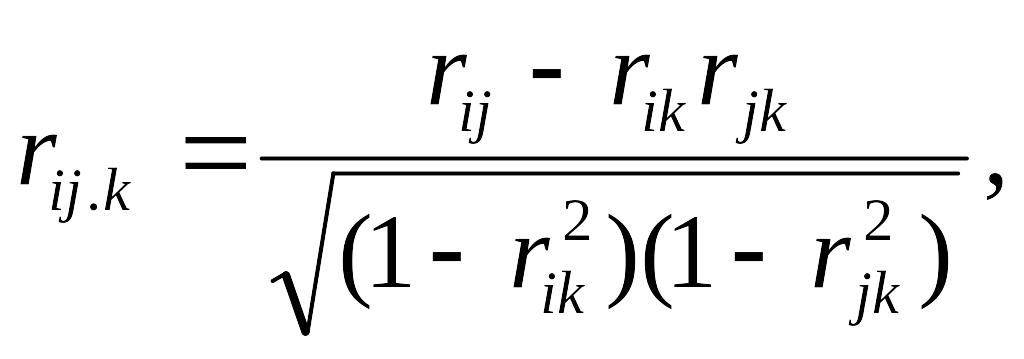_(1.7)

де r_ij, r_jk, r_ik – парні коефіцієнти кореляції. коефіцієнт r_ij.k називається частинним чи умовним коефіцієнтом кореляції величин (x_і , x_j) без врахування впливу x_k. Так як виключений вплив тільки однієї змінної, то коефіцієнт кореляції називається частинним коефіцієнтом кореляції першого порядку.

У випадку чотирьох змінних можна обчислити частинні коефіцієнти кореляції першого і другого порядків. Коефіцієнти другого порядку отримуються в результаті послідовного виключення парних коефіцієнтів кореляції, а потім коефіцієнтів кореляції першого порядку.

Так, для чотирьох випадкових величин х₁, х₂, х₃, х₄ коефіцієнти кореляції першого порядку обчислюються за попередньою формулою, а коефіцієнт кореляції другого порядку можна обрахувати за формулою:

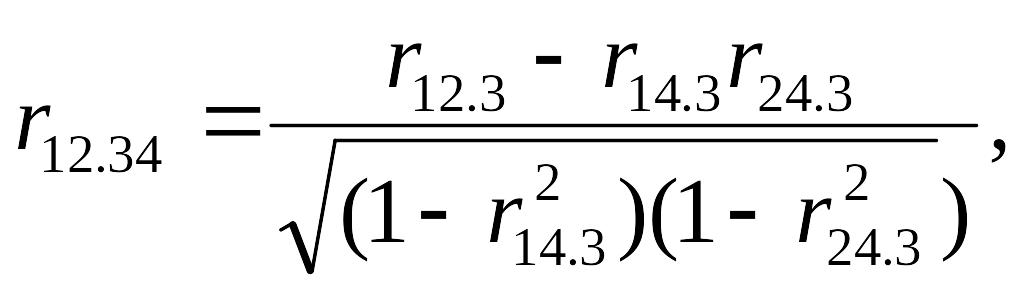_(1.8)

де r_12.3, r_14.3, r_24.3 – частинні коефіцієнти кореляції першого порядку.

Частинні коефіцієнти вищих порядків обчислюються аналогічно.

1.4. Множинний коефіцієнт кореляції

Щільність зв’язку у випадку багатофакторної регресії оцінюється кореляційним відношенням, яке в випадку лінійного зв’язку називається множинним коефіцієнтом кореляції і позначається R. Коефіцієнт множинної кореляції є міра залежності між однією випадковою змінною і сукупністю інших. Коефіцієнт множинної кореляції виражає точність прогнозу залежності випадкової змінної по лінійному рівнянню регресії. Коефіцієнт множинної кореляції можна виразити через коефіцієнт парної кореляції. У випадку трьохзмінних маємо:

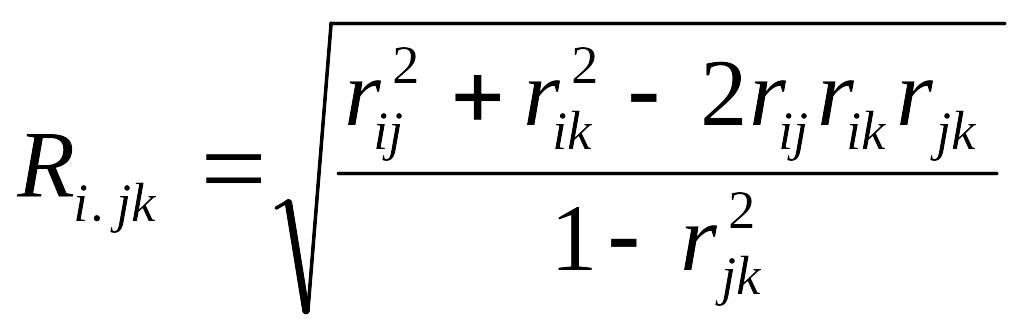(1.9)

Коефіцієнт множинної кореляції зручно обчислювати за формулою:

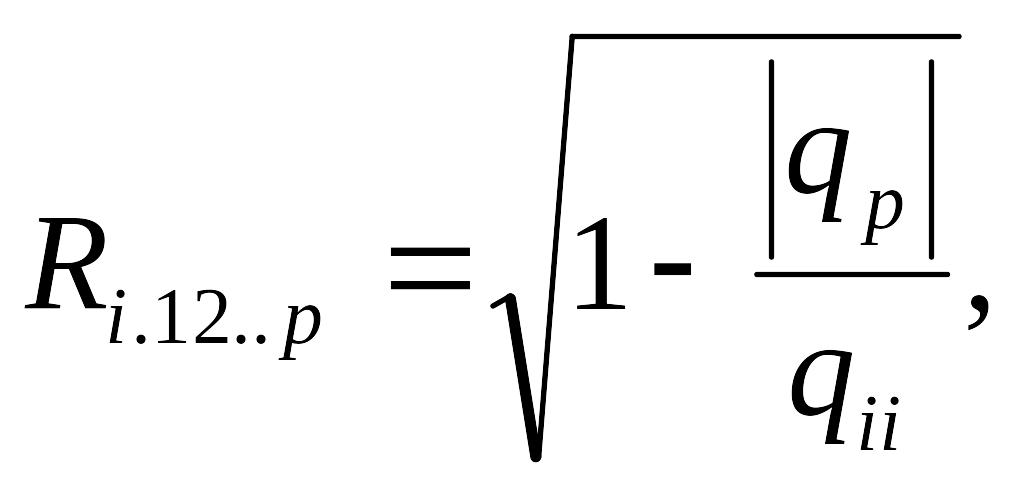(1.10)

де - детермінант матриці q_p

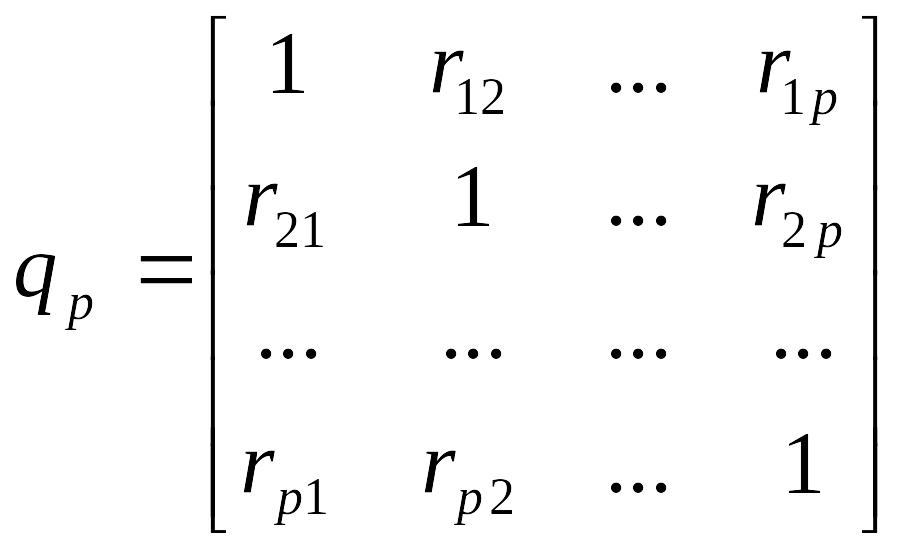, де p – кількість ознак,

- алгебраїчне доповнення елемента r_ay тієї ж матриці.

Множинний коефіцієнт кореляції знаходиться в межах 0≤R≤1. За допомогою множинного коефіцієнта кореляції роблять висновок про щільність взаємозв’язку, але не про його напрям. Величина R² називається вибірковим множинним (сукупним) коефіцієнтом детермінації, показує яку долю варіації досліджуваної змінної пояснює варіація інших змінних.

Можна показати, що множинний коефіцієнт кореляції значимо відрізняється від нуля, якщо значення статистики

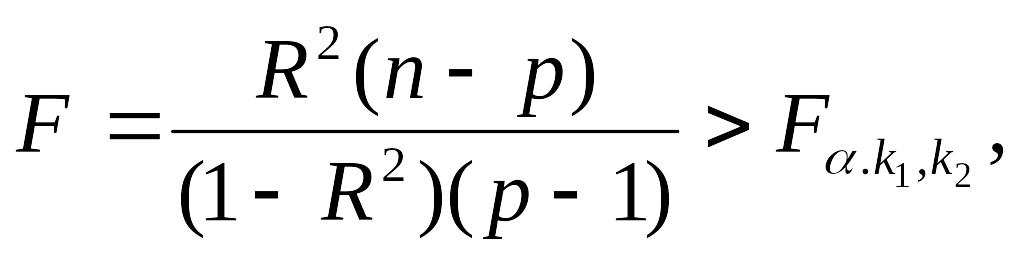(1.11)

де - табличне значення F-критерія на рівні значущі α при числі степенів свободи k₁ =p - 1 і k₂ =n – p.

Розділ 2. Розв’язання маркетингової задачі за допомогою кореляційного аналізу

Нерідко в практиці маркетингу необхідно з’ясувати міру зв’язку між деякими ознак-факторами. Для цього доцільно використовувати коефіцієнт кореляції. Сформулюємо наступну ситуацію.

Нехай певну фірму цікавить наступне питання. Чи існує взаємозв’язок між відстанню до центру міста, кількістю відвідувачів на місяць та кількістю місць відпочинку(боулінг, каток, більярд, кафе, кінозали та ін.) розважальних центрів? Спробуємо дати відповідь на це питання, використовуючи кореляційний аналіз.

Позначимо змінні наступним чином:

х – відстань до центру міста (км);

у – кількість відвідувачів на місяць (чол.);

k – кількість місць відпочинку (шт.).

Запишемо початкові дані у вигляді таблиці 2.1, в якій введені додаткові стовбці, що необхідні для знаходження коефіцієнта кореляції по формулі (1.4):

Таблиця 2.1

Розрахунок парних коефіцієнтів кореляції

№ з/п	х	y	k
1	15	3189	8	1,6	-38,7	-82	2,56	1497,69	6724
2	11	3721	9	-2,4	493,3	-81	5,76	243345	6561
3	17	2975	7	3,6	-252,7	-83	12,96	63857,3	6889
4	22	2744	9	8,6	-483,7	-81	73,96	233966	6561
5	9	4089	7	-4,4	861,3	-83	19,36	741838	6889
6	14	2955	11	0,6	-272,7	-79	0,36	74365,3	6241
7	18	3094	9	4,6	-133,7	-81	21,16	17875,7	6561
8	4	3789	13	-9,4	561,3	-77	88,36	315058	5929
9	8	2865	9	-5,4	-362,7	-81	29,16	131551	6561
10	16	2856	8	2,6	-371,7	-82	6,76	138161	6724
Сума	134	32277	90			-810	260,4	1961514	65640
Середнє	13,4	3227,7	9

Продовження табл. 2.1

№ з/п
1	-61,92	-131,2	3173,4
2	-1183,92	194,4	-39957,3
3	-909,72	-298,8	20974,1
4	-4159,82	-696,6	39179,7
5	-3789,72	365,2	-71487,9
6	-163,62	-47,4	21543,3
7	-615,02	-372,6	10829,7
8	-5276,22	723,8	-43220,1
9	1958,58	437,4	29378,7
10	-966,42	-213,2	30479,4
Сума	-15167,8	-39	893

Обчислимо емпіричні значення парних коефіцієнтів кореляції, використовуючи формулу (1.4). Результати обчислень подано в таблиці 2.2.

Таблиця 2.2

Парні коефіцієнти кореляції

Коефіцієнт кореляції	Значення коефіцієнта
r (xy)	-0,823
r (xk)	-0,441
r (yk)	0,19

Оскільки два коефіцієнти кореляції є від’ємними, а третій додатнім, можна зробити висновок, що взаємозв’язок є і обернений, і прямий, а саме:

• чим більше відстань від центру міста, тим менше відвідувачів, і навпаки

• чим більше відстань від центру міста, тим менше повинно бути місць відпочинку і навпаки

• чим більше відвідувачів, тим більша кількість місць відпочинку.

Отже, перш за все, ми повинні зорієнтувати свою увагу на залежності віддаленості від центру міста, та при побудові нового розважального центру потрібно орієнтуватися на якнайменшу відстань.

Таблиця 2.3

Оцінка значимості коефіцієнта кореляції

tрозр	tкрит
4,582	2,896
1,554	2,896
0,612	2,896

Визначимо критичні значення для отриманих коефіцієнтів кореляції по формулі (1.6). При знаходженні критичних значень для обчисленого коефіцієнта лінійної кореляції число ступенів свободи розраховується як k = n – 2 = 8, а рівень значущості ( ) приймемо за 0,01. Результати обчислень подано в таблиці 2.3, з якої слідує, що для одного парного коефіцієнта виконується наступна умова: t_розр > t_крит. Отже, можна зробити висновок, що гіпотеза про нульове значення коефіцієнтів кореляції в генеральній сукупності не підтверджується, тобто в генеральній сукупності існує лінійний зв’язок. Для двох парних коефіцієнтів виконується умова: t_розр < t_крит,,Отже, можна зробити висновок, що між ними існує нелінійний зв’язок.

Для того, щоб виключити можливий вплив інших змінних на обраховані в таблиці 2.2 парні коефіцієнти кореляції, обчислимо по формулі (1.7) частинні коефіцієнти. Результати запишемо в таблицю 2.4.

Таблиця 2.4

Частинний коефіцієнт кореляції

Частинний коефіцієнт кореляції	Значення коефіцієнта
r (xy.k)	-0,839
r(xk.y)	-0,51
r(yk.x)	-0,338

Коефіцієнт r (xy.k):

Цей коефіцієнт оцінює щільність лінійного кореляційного зв’язку між відстанню до центру міста та кількістю відвідувачів при фіксованому значенні місць відпочинку. Іншими словами, r (xy.k) оцінює залежність на результативну ознаку зміни лише кількості місць відпочинку. Аналогічно для r(xk.y) і r(yk.x).

Для того, щоб зробити висновки, розглянемо зведену таблицю 2.5.

Таблиця 2.5

Порівняння парних та частинних коефіцієнтів кореляції

Парний коефіцієнт кореляції	Значення коефіцієнта	Частинний коефіцієнт кореляції	Значення коефіцієнта
r (xy)	-0,823	r (xy.k)	-0,839
r (xk)	-0,441	r(xk.y)	-0,51
r (yk)	0,19	r(yk.x)	-0,338

Як бачимо з таблиці, частинний коефіцієнт кореляції залежності кількості місць відпочинку та кількості відвідувачів при сталій відстані від центру майже співпадає з відповідним парним коефіцієнтом (-0,823 і -0,839). Це означає, що взаємозв’язок між кількістю місць відпочинку та кількістю відвідувачів не опосередковується, та не посилився вплив, з віддаленістю від центру. В невеликій мірі посилився вплив фактору кількості відвідувачів на взаємозв’язок між кількістю місць відпочинку та віддаленістю від центру(з -0,441 до -0,51). Якщо розглянути зв'язок між кількістю відвідувачів та віддаленістю від центру, то бачимо, що цей взаємозв’язок опосередковується, та посилився вплив при сталій кількості місць відпочинку. Перевіримо значимість частинних коефіцієнтів.

Таблиця 2.6

Оцінка значимості коефіцієнта кореляції

tф	tкрит
3,079	2,896
-1,568	2,896
2,95	2,896

Оскільки t_ф1> t_крит та t_ф3> t_крит то наявність взаємозв’язку між віддаленістю від центру та кількістю відвідувачів і між кількістю відвідувачів та кількістю місць відпочинку підтверджується. Не підтверджується взаємозв’язок між відстанню від центру та кількістю місць відпочинку: t_ф2<t_крит..