Министерство образования Российской Федерации.

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ

РАДИОТЕХНИКИ, ЭЛЕКТРОНИКИ И АВТОМАТИКИ

( ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ.)

Курсовая работа.

Тема: ” Игры с нулевой суммой ”

по дисциплине “Теории принятия решения ”.

Выполнил: Блажко Евгений Эдуардович Группа: ИС-1-01 Факультет: Кибернетики Научный руководитель: профессор Струченков В.И.

Москва. 2004 г.

1. Игры с чистыми стратегиями.

Игра двух лиц с нулевой суммой в матричной форме занимает центральное место в современной теории игр. Пусть имеется два игрока. В распоряжении первого игрока имеется всего n возможных ходов i=1,2,3,...,n; в распоряжении второго игрока имеется m возможных ходов j=1,2,3,...,m. Эти возможные ходы называются чистыми стратегиями игроков.

Оба игрока делают одновременно по одному ходу, после чего партия считается законченной. Если первый игрок делает ход i, а второй  ход j, то первый игрок получает выигрыш, равный a_ij. Очевидно, что выигрыш второго игрока равен -a_ij. Эти данные можно записать в виде матрицы

,

в которой строки соответствуют ходу первого игрока, а столбцы  ходу второго игрока. Эта матрица носит название матрицы выигрышей (платёжной матрицы).

Пусть первый игрок выбирает ход i. В наихудшей для него ситуации он выиграет min_ja_ij.

Стремясь сделать свой минимальный выигрыш максимальным, он выбирает свой ход из условия max_i min_j a_ij. Такая стратегия называется максиминной.

Аналогично, второй игрок, выбирая ход j, в наихудшей для себя ситуации проигрывает max_i a_ij. Стремясь сделать свой максимальный проигрыш минимальным, он должен выбирать свой ход из условия min_j max_i a_ij. Такая стратегия называется минимаксной.

Существует соотношение между max_i min_j a_ij и min_j max_i a_ij :

max_i min_j a_ij  min_j max_i a_ij

Если обе величины равны для пары i=I, j=J, говорят, что игра имеет седловую точку или решение I,J и единственную цену a_IJ. Если первый игрок знает предстоящий ход второго, и обратно, то оптимальные стратегии для такой игры не имеют смысла.

2. Игры со смешанными стратегиями.

Смешанной стратегией первого игрока называется вектор  где p_i – представляет собой вероятность применения первым игроком чистой стратегии.

Аналогично смешанная стратегия второго игрока представляет собой вектор где q_j представляет собой вероятность применения вторым игроком чистой стратегии. Цена игры должна теперь определяться математическим ожиданием выборочных значений выигрыша (проигрыша) игроков с учетом вероятностей появления различных стратегий  игроков за период игры.

В игре со смешанными стратегиями первый игрок стремится максимизировать минимум математического ожидания посредством выбора p₁,p₂,…,p_n.

Тогда как стремится минимизировать путем выбора q₁,q₂,…,q _m.

Для любой заданной матрицы выигрышей

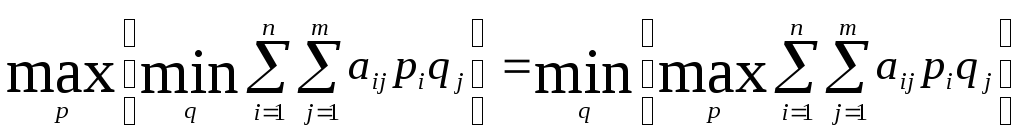
Эта величина называется ценой V игры.