11. Какие применяются способы для определения площадей земельных участков. Точность определения площади

На планах и картах площади могут быть определены аналитическим, геометрическим или механическим способом.

Площадь ЗУ вычисляют аналитическим способом по плоским прямоугольным координатам межевых знаков, установленным в поворотных точках его границы, полученным в результате соответствующих полевых измерений и вычислительных работ.

Аналитический способ предполагает известными координаты x_i у_i{ (i = 1, 2, . . . , n) вершин замкнутого многоугольника. Величину S пло­щади определяют по известной формуле

2S=∑x_i(y_i+1-y_i-1)=∑ y_i(x_i-1-x_i+1),которую можно подвернуть различным преобразованиям.

Точность определения площади в этом случае зависит лишь от точ­ности определения координат точек. Так, при углах, измеренных с точ­ностью порядка 1', и линиях — порядка 1 : 2000, ошибка в площади будет около 1 : 1500.

Геометрический способ заключается в разделении фигуры на не­сколько таких частей, площади которых определяют по удобным форму­лам (треугольник, прямоугольник, трапеция).

Частным видом этого способа является использование различных палеток, нанесенных на прозрачном материале, в частности палеток в виде системы параллельных линий, удаленных друг от друга на одинако­вом расстоянии, а также в виде сетки квадратов со сторонами от 2 до 10 мм (в зависимости от размера определяемой площади). В случае первой па­летки эта площадь делится на трапеции с постоянной высотой h, равной расстоянию между параллельными линиями. Длину l средней линии каждой трапеции измеряют и определяют площадь по формуле

S=h∑l_i

Для палетки со сторонами квадрата, равными а, площадь определяют по формуле

S=Na² + Δa

где N — число целых квадратов, уложившихся в измеряемой площади, а Аа — дробная часть квадрата (оценивается на глаз).

Относительную ошибку определения площади палеткой можно при­нять равной 1: 50.

Механический способ измерения площадей основан на использовании специального прибора — планиметра, позволяющего определять площадь с относительной ошибкой порядка 1:300.

Когда площадь меньше 10 см² , то применяют аналитический метод, когда больше – механический.

Определение площади планиметром – определение площади плоской фигуры путем обвода ее по контуру. Планиметры бывают: полярные и линейные.

Для того чтобы определить цену деления планиметра, необходима фигура с известной площадью, ее нужно обвести 3-4 раза.

P=p/n

p-известная площадь фигуры, n- количество делений планиметра, полученное при обводе фигуры. Определяется до 4 значимых цифр. Значимы цифры – все цифры кроме нуля, которые находиться с левой стороны.

12. Ориентирование линий местности. Связь между углами ориентирования.

Ориентировать линию – это значит найти её направление относительно какого-либо другого направления, принимаемого за исходное. Горизонтальный угол между исходным направлением и ориентируемой линией называется ориентирным углом.

В качестве исходных в геодезии принимают направления истинного меридиана, магнитного меридиана либо осевого меридиана зоны.

В зависимости от выбранного истинного направления ориентирным углом может быть истинный азимут, магнитный азимут, дирекционный угол или румб.

Угол, измеряемый по ходу часовой стрелки от северного направления меридиана до заданного направления, называется азимутом.

Если исходным направлением служит геодезический меридиан, то азимут называют геодезическим азимутом. Если – астрономический, то - астрономическим азимутом. Обобщением обоих понятий служит термин - географический азимут или просто - азимут.

Значения азимута лежат в пределах от 0° до 360°. На рис. 3.1, а обозначено: С – северное направление меридиана, угол А₁ – азимут направления на точку 1 и А₂ – азимут направления на точку 2.

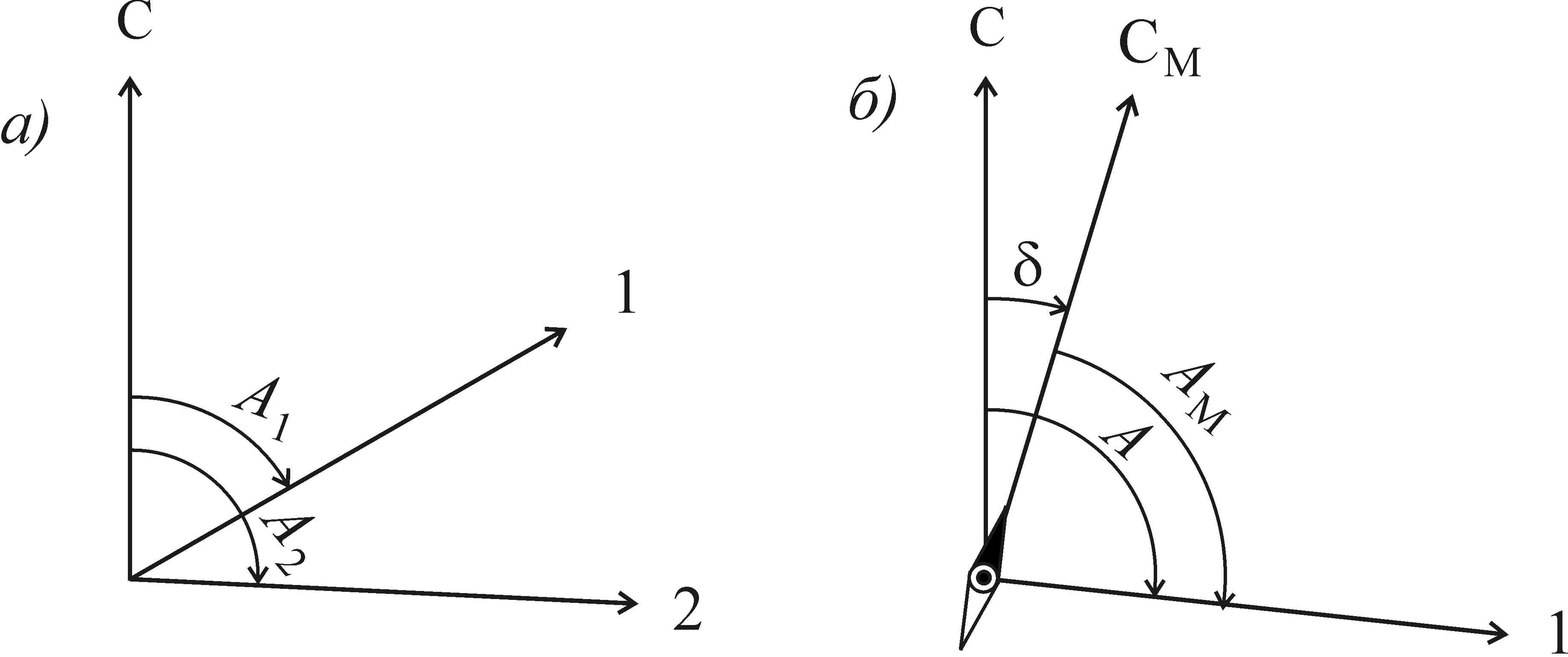
Рис. 3.1. Углы ориентирования: а - азимуты географические; б - магнитный азимут

На местности азимут заданного направления можно определить астрономическим методом - измерив горизонтальный угол между направлением на небесное светило (Солнце, звезду) и заданным направлением. Зная азимут светила, вычисляемый с использованием астрономического ежегодника, и измеренный угол, соображают азимут заданного направления.

Угол, отсчитываемый от северного направления магнитной стрелки до заданного направления, называется магнитным азимутом.

Магнитная стрелка компаса отклоняется от направления истинного меридиана на угол d, который называется склонением магнитной стрелки (рис. 3.1, б).

Если северный конец магнитной стрелки отклоняется от меридиана к востоку, то склонение называют восточным и считают положительным, а если - к западу, то называют западным и считают отрицательным.

Азимут с магнитным азимутом связывает формула:

где А - азимут, А_м - магнитный азимут и d – склонение магнитной стрелки.

Магнитные азимуты в геодезии измеряют буссолью (рис. 3.2). Однако точность этих измерений невысока (несколько минут), так как склонение магнитной стрелки непостоянно. На территории России оно меняется от места к месту в пределах от –15° до 25°. В аномальных районах (например, в районе Курской магнитной аномалии) эти изменения так велики, что магнитной стрелкой пользоваться нельзя. Кроме того, склонение изменяется во времени, испытывая суточные, годовые и вековые изменения.

Углом ориентирования, применяемым при использовании системы плоских прямоугольных координат Гаусса-Крюгера, является дирекционный угол.

Дирекционным углом называется угол между северным направлением осевого меридиана или линии ему параллельной и заданным направлением (рис. 3.3).

Угол g между северным направлением меридиана и направлением оси абсцисс х прямоугольных координат (то есть линии, параллельной осевому меридиану) называется сближением меридианов.

Рис. 3.3. Углы ориентирования: а - дирекционные углы a₁, a₂; б - азимут A и дирекционный угол a

При отклонении оси абсцисс от меридиана к востоку, сближение меридианов считают положительным, а при отклонении к западу - отрицательным. При этом справедлива формула (рис. 3.3 б)

А = a + g,

где a - дирекционный угол, g - сближение меридианов.

Приближенно сближение меридианов равно

g = Dl sinj,

где Dl = l-l₀, причем l -долгота географического данной точки и l₀ - долгота осевого меридиана; j - широта точки.

На рис. 3.4 показано соотношение между азимутами и дирекционными углами в пределах одной координатной зоны. Легко заметить, что для точек, расположенных к востоку от осевого меридиана зоны, сближение меридианов положительное, а к западу – отрицательное. При этом дирекционные углы в разных точках прямой линии равны a₁ = a₂ = a₃. Поэтому обратный дирекционный угол в точке 3 отличается от прямого в точке 1 ровно на 180°, то есть a_1-3 = a_3-1 ± 180°. Азимуты же в разных точках прямой различаются: А₁ ¹ А₂ ¹ А₃, что обусловлено различием сближения меридианов. Поэтому и А_1-3 ¹ А_3-1 ± 180°.

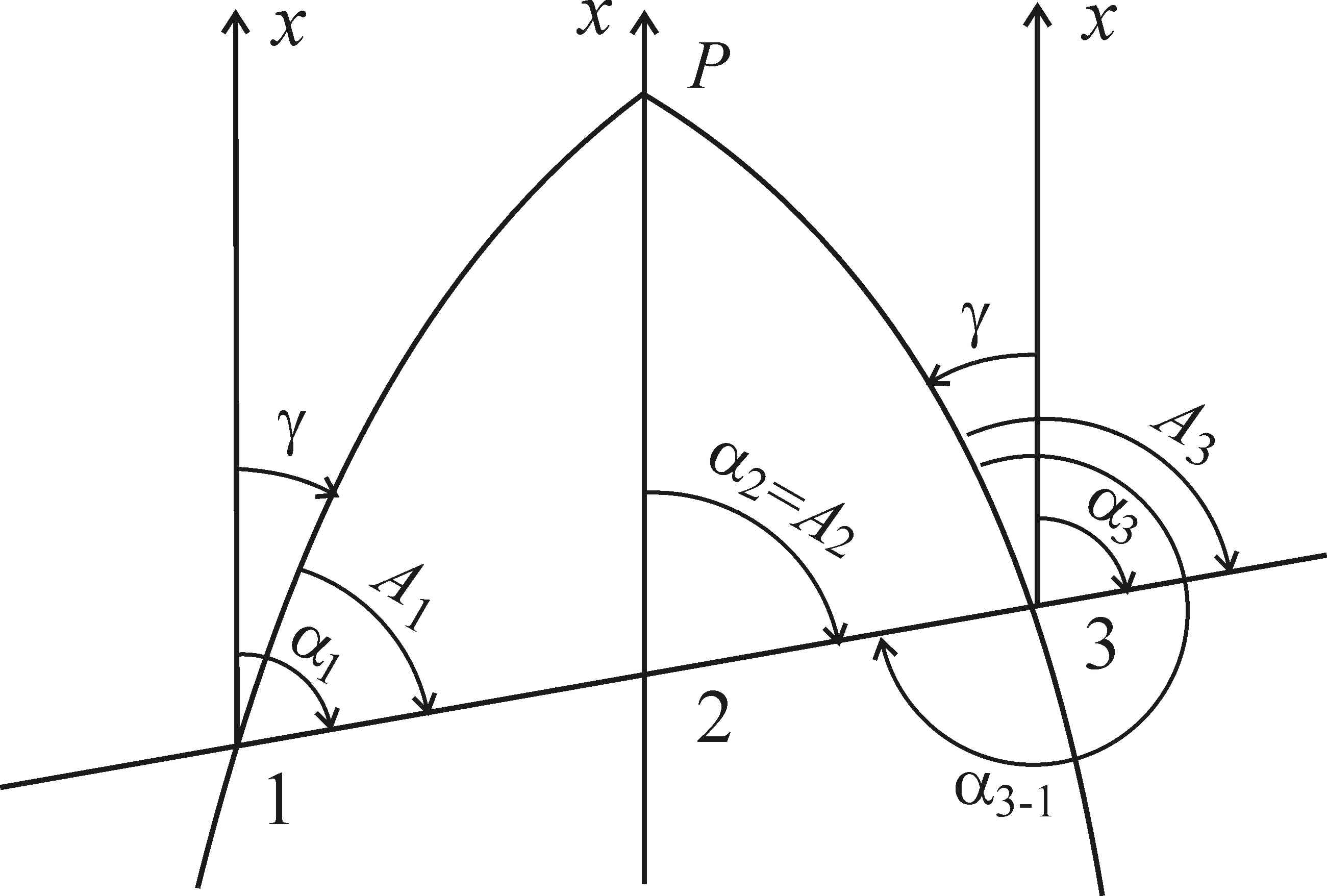
Рис. 3.4. Связь между азимутами и дирекционными углами: 1 – в западной половине зоны; 2 – на осевом меридиане; 3 – в восточной половине зоны; Р – полюс; 1Р, 3Р – меридианы; 2Р – осевой меридиан.

При использовании местной системы прямоугольных координат направление оси абсцисс x не связано с направлением осевого меридиана координатной зоны, и тогда дирекционные углы отсчитывают от положительного направления оси абсцисс х.

В практике вычислений находят применение также вспомогательные углы ориентирования – румбы. Румбом называют острый угол, измеряемый от ближайшего направления меридиана (северного или южного). Румбу приписывают название координатной четверти (СВ, ЮВ, ЮЗ, СЗ), в которой расположено заданное направление. Например, для a = 240°36¢ румб равен r = ЮЗ: 60°36¢.