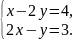Ход урока
Структура урока |
Деятельность учителя |
Деятельность учащихся |
||||||
Организационный момент |
- Здравствуйте, ребята, садитесь. Открываем тетради, записываем сегодняшнюю дату 11.02.2013г. и тему урока «Геометрическая интерпретация системы двух линейных уравнений с двумя переменными». |
Ученики приветствуют учителя. Садятся на свои места, открывают тетради и записывают дату, тему урока. |
||||||
Постановка целей и задач урока |
- Сегодня на уроке мы выясним,
|
Ученики слушают учителя. |
||||||
Актуализация опорных знаний. |
- Повторим ранее пройденный материал. Ответьте на следующие вопросы: - Что называется графиком уравнения с двумя переменными?
- Укажите уравнения, которые являются линейными уравнениями с двумя переменными:
- Как задается линейное уравнение в общем виде?
- Что является графиком линейного уравнения?
-
Если в линейном уравнении
-
Если
в линейном уравнении
,
-
Принадлежит ли точка
-
Назовите любую точку, принадлежащую
графику уравнения
|
Слушают, отвечают.
- Графиком уравнения с двумя переменными называется множество всех точек на координатной плоскости, координаты которых являются решениями этого уравнения.
- Линейными уравнениями являются уравнения а), в).
- Линейное уравнение имеет следующий вид: .
- Графиком линейного уравнения является прямая. -
Графиком является прямая, параллельная
оси
-
Графиком является прямая, параллельная
оси
-
Точка
- Точки (2;-3), (5;-8) принадлежат графику уравнения |
||||||
Введение нового материала с использованием элементов модульной технологии. |
-
Рассмотрим систему двух линейных
уравнений с двумя переменными
Если
координаты точки
Если точка удовлетворяет второму уравнению системы, то точка лежит на прямой, которая определяется вторым уравнением. Значит, если координаты точки удовлетворяют обеим уравнениям системы, то точка лежит на обеих прямых. Поскольку решить систему значит найти все ее решения либо доказать что их нет, таким образом, решением исходной системы и являются координаты их общей точки . - Возможны три случая расположения двух прямых в координатной плоскости, определяемых уравнениями системы: прямые пересекаются в одной точке; прямые совпадают; прямые не имеют общих точек. Можно, это, конечно, определять путем построения. Данный способ решения системы является графическим. Решение таким способом обычно занимает много времени. - Как вы думаете, а существует ли другой способ определения взаимного расположения двух прямых? - Оказывается, что существует. Но для этого должны выполняться следующие условия:
- Способ определения взаимного расположения графиков линейных уравнений в координатной плоскости на основании связи между коэффициентами линейных уравнений называется аналитическим способом. -
Таким
образом, геометрическая интерпретация
системы двух линейных уравнений с
двумя переменными, в каждом из которых
хотя бы один из коэффициентов при
переменных не равен
- Рассмотрим несколько примеров и определим, как в каждом из данных случаев будут расположены прямые. а)
Решение: а)
б)
в)
и
|
Ученики слушают и дополняют.
Постановка проблемной ситуации. Ученики выдвигают гипотезу. Учащиеся записывают в тетрадь оформляя в виде таблицы:
Ученики делают записи в тетрадь. |
Закрепление полученных знаний в процессе решения тренажерных упражнений с применением модульной технологии (Приложение 1).
Цель: формирование умений применения геометрического способа определения взаимного расположения двух прямых в координатной плоскости.
Номер учебного элемента |
Задание |
Указание учителя |
УЭ-1 |
Изобразите прямые, уравнения которых записаны в системе, и укажите число решений системы: 1)
|
Для решения примеров из данного учебного элемента вам необходимо будет построить графики двух линейных уравнений в координатной плоскости и определить количество решений. |

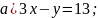
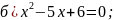
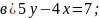
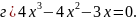
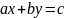 ,
,
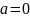 ,
как расположен график этого уравнения
в координатной плоскости?
,
как расположен график этого уравнения
в координатной плоскости?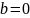 ,
как расположен график этого уравнения
в координатной плоскости?
,
как расположен график этого уравнения
в координатной плоскости?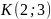 графику уравнения
графику уравнения
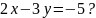
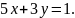
 .
.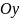 .
.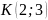 принадлежит графику уравнения
принадлежит графику уравнения
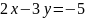 .
.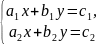 .
Каждое
уравнение этой системы является
уравнением прямой.
.
Каждое
уравнение этой системы является
уравнением прямой.
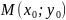 удовлетворяют первому уравнению
системы, то точка
удовлетворяют первому уравнению
системы, то точка
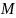 лежит на прямой, которая определена
первым уравнением.
лежит на прямой, которая определена
первым уравнением.
 истема
имеет единственное решение, если:
истема
имеет единственное решение, если:
 .
.
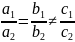 .
.
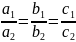 .
.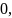 есть
либо пара пересекающихся прямых,
параллельных прямых, совпадающих
прямых.
есть
либо пара пересекающихся прямых,
параллельных прямых, совпадающих
прямых.
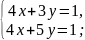 б)
б)
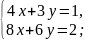 в)
в)
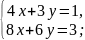
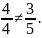 Следовательно,
система имеет единственное решение.
Следовательно,
система имеет единственное решение.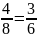 и
и
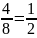 .
Следовательно, система имеет бесконечно
много решений.
.
Следовательно, система имеет бесконечно
много решений.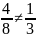 .
Следовательно, система не имеет
решений.
.
Следовательно, система не имеет
решений.

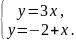 2)
2)
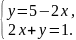 3)
3)