1.2.5Задача № 7. Моделирование непрерывной разливки стали.

Наиболее полно непрерывную разливку стали моделируют по трем критериям: Рейнольдса , Вебера и Фруда . Поток жидкого металла всегда турбулентен, поэтому от величины критерия Рейнольдса никакие характеристики потока жидкости практически не зависят. В этом случае моделирование проводят по равенству двух критериев. – Вебера и Фруда. Критерий Вебера можно записать следующим образом , а критерий Фруда - , где - плотность жидкости; - характерный размер потока; - поверхностное натяжение; - скорость потока жидкости; - ускорение силы тяжести. Как видно из приведенных выражений, критерий Вебера содержит две характеристики жидкости , и одну характеристику модели – ее размер . Критерий Фруда содержит две характеристики жидкости – скорость потока и характерный размер .

Расчет модели непрерывной разливки стали производится в следующей последовательности:

а) выбираем моделирующую жидкость с определенными значениями и ;

б) из условия равенства критериев Вебера в натуре и на модели находим характерный размер модели; для этого используем следующие выражения;

или , (1)

отсюда ; (2)

в) из условия равенства критериев Фруда в натуре и на модели находим скорость потока расплава на модели ; для этого используем следующие выражения:

или , (3)

отсюда (4)

г) при непрерывной разливке стали металлический расплав заливают в кристаллизатор прямоугольного сечения, одна из сторон которого принята за характерный размер ; отношения площадей сечения и двух кристаллизаторов с размерами и , очевидно, пропорциональны отношению квадратов размеров и

(5)

Расход жидкости , м³/ч или м³/с, через кристаллизатор пропорционален произведению скорости потока на площадь сечения

(6)

Используя выражение (4) и формулу (6) получим

. (7)

В задаче используются физические свойства стали , , размер кристаллизатора и расход металла в нем , м³/ч. используя эти данные, необходимо по выбранной моделирующей жидкости найти размер кристаллизатора модели и расход моделирующей жидкости в м³/ч, а также л/мин.

Таблица 2.7 – Многовариантные задания к задаче № 7 по вычислению характеристик модели непрерывной разливки стали.

Вариант	Сталь				Модель
	ρн , кг/м3	н, Н/м	Qн, м3/ч	lн, мм	жидкость	ρм , кг/м3	м, Н/м
1	2	3	4	5	6	7	8
1	7000	1,2	3,88	400х100	Н2О – КCl	1750	72,110-3
2	7020	1,23	4,5	500х100	Н2О – КCl	1210	83,110-3
3	7040	1,26	5,2	600х100	Н2О – КCl	1300	72,510-3
4	7060	1,29	5,75	700х100	Н2О – КCl	1520	74,610-3
5	7080	1,32	6,12	800х100	Н2О – КCl	1630	26,810-3
6	7100	1,35	6,6	900х100	Н2О – КCl	1930	74,010-3
7	7120	1,38	6,9	1000х100	Керосин	800	25,910-3
8	7140	1,41	7,1	1100х100	Масло ВМ-1	912	34,010-3
9	7160	1,44	6,05	1200х100	Масло веретенное	870	32,910-3
10	7180	1,47	4,19	400х120	Масло касторовое	950	29,010-3
11	7200	1,5	4,92	500х120	Н2О + глицерин	1260	64,610-3
1	2	3	4	5	6	7	8
12	7220	1,53	5,55	600х120	–″–	1255	64,910-3
13	7240	1,56	6,18	700х120	–″–	1236	65,910-3
14	7260	1,59	6,75	800х120	–″–	1220	66,610-3
15	7280	1,62	7	900х120	–″–	1185	68,210-3
16	7300	1,65	7,2	1000х120	–″–	1146	69,610-3
17	7320	1,68	7,5	1100х120	Керосин + ВМ-1	837	26,610-3
18	7340	1,71	7,7	1200х120	–″–	870	29,410-3
19	7360	1,74	7,85	1400х120	–″–	892	30,910-3
20	7380	1,77	7,05	1500х120	–″–	906	31,810-3
21	7410	1,8	13,9	500х150	Н2О – 100С	1000	74,210-3
22	7440	1,82	5,8	600х150	Н2О –300С	996	71,210-3
23	7470	1,84	6,5	700х150	Н2О – 500С	988	67,710-3
24	7490	1,86	6,8	800х150	Н2О –600С	983	62,210-3
25	7100	1,87	7,2	900х150	Н2О –700С	978	64,210-3

Пример решения варианта 1.

1. По формуле (2) характерный размер модели

2. Второй размер кристаллизатора модели вычислим следующим образом:

.

Из формулы (7) найдем расход жидкости модели

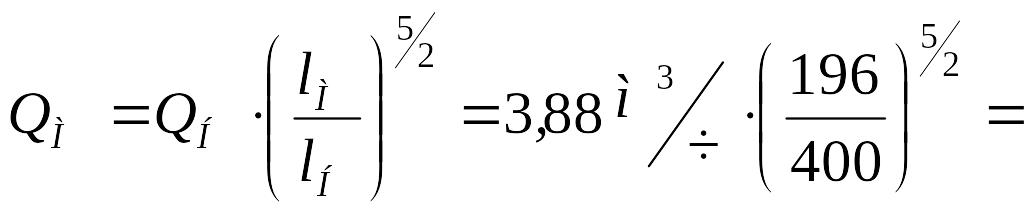
пересчитаем расход жидкости из м³/ч в л/мин:

1 м³/ч=1000 л/ 60 мин=1,67 л/мин;

поэтому л/мин.

Ответ: размер модели кристаллизатора 196 49 мм

расход жидкости на модели 10,9 л/мин.