§ 1. Структурный анализ плоских механизмов

1.1. Основные понятия и определения

Механизмом называется система твердых тел, предназначенная для передачи и преобразования заданного движения одного или нескольких тел в требуемые движения других твердых тел.

Звено - твердое тело или система жестко связанных тел, входящих в состав механизма.

Входное звено (ведущее) - звено, которому сообщается заданное движение и соответствующие силовые факторы.

Выходное (ведомое) звено - то, на котором получают требуемые движение и силы.

Кинематическая цепь - система звеньев, образующих между собой кинематические пары.

Кинематическая пара - подвижное соединение двух звеньев, допускающее их определенное относительное движение.

Стойка - звено, которое при исследовании механизма принимается за неподвижное.

Число степеней свободы или подвижность механизма - число независимых обобщенных координат, однозначно определяющее положение всех его звеньев на плоскости или в пространстве.

При работе механизма все его звенья (за исключением стойки), перемещаются в пространстве и в каждый момент времени занимают определенные положения. Чтобы определить положение какого-либо звена, надо знать координаты других звеньев, например углы поворота или линейные перемещения. Независимые между собой координаты, определяющие положение всех звеньев механизма относительно стойки, называют обобщенными координатами механизма. Таким параметром может быть, например, угол поворота ₁ кривошипа О₁А (рис. 2).

Итак, если механизм имеет одну степень свободы, то определенному положению его начального звена (как правило, оно же является входным) соответствует одно определенное положение остальных звеньев. Поэтому степень подвижности механизма в большинстве случаев, численно равна числу входных звеньев механизма.

Начальное звено - звено, координата которого принята за обобщенную.

Начальная кинематическая пара - пара, относительное положение звеньев, в которой принято за обобщенную координату.

12. Определение степени подвижности плоских механизмов

Степень подвижности плоских механизмов определя­ется по формуле П. Л. Чебышева:

где W — степень подвижности (подвижность) механизма; п — число под­вижных звеньев механизма; р₅ — число кинематических пар V класса (низших); р₄ — число кинематических пар IV класса (высших). Степень подвижности механизма определяет число входных (ве­дущих) его звеньев, т. е. количество звеньев, которым не­обходимо задать движение, чтобы все остальные звенья двигались по однозначно определенным законам.

1.3. Структурная классификация механизмов по Ассуру – Артоболевскому

Структурной классификацией механизмов называется разделение их на группы и классы по общности структуры.

Впервые научно обоснованная, рациональная классификация плоских механизмов была предложена в 1914 г. Русским ученым Л.В. Ассуром.

Дальнейшее развитие структурная классификация плоских механизмов получила в работах академика И.И. Артоболевского, трудами которого ей была придана стройная последовательность, позволившая четко увязать классификацию с методами кинематического и силового расчета.

Согласно теории Ассура – Артоболевского плоский механизм с низшими парами (только вращательными или поступательными) может быть образован путем последовательного присоединения к первичным механизмам структурных групп Ассура.

Первичным механизмом (ПМ) называется совокупность входного звена и стойки, образующих кинематическую пару пятого класса. В классификации Ассура первичный механизм относится к I классу, I порядку. Подвижность ПМ равна единице.

Группой Ассура (структурной группой) называется кинематическая цепь, образованная только подвижными звеньями, обладающая нулевой подвижностью и не распадающаяся на более простые цепи.

Для плоских механизмов с низшими парами структур­ная формула групп Ассура имеет вид:

откуда

Поскольку в группе не может быть дробное число кине­матических пар, то группы Ассура должны состоять только из четного числа звеньев.

Чтобы из механизма выделять структурные группы, необходимо помнить их основные признаки, вытекающие из определения:

а) число звеньев в группе должно быть четным;

б) степень подвижности группы всегда равна нулю.

Элементарная (простейшая) группа, состоящая из двух звеньев и трех кинематических пар, называется группой II класса II порядка, или двух поводковой группой. Повод­ком называется звено, входящее в группе в две кинемати­ческие пары, одна из которых свободная и служит для присоединения к одному из подвижных звеньев механизма или к стойке. Порядок структурных групп определяется числом поводков.

Группы 2 класса показаны на рис. 1.

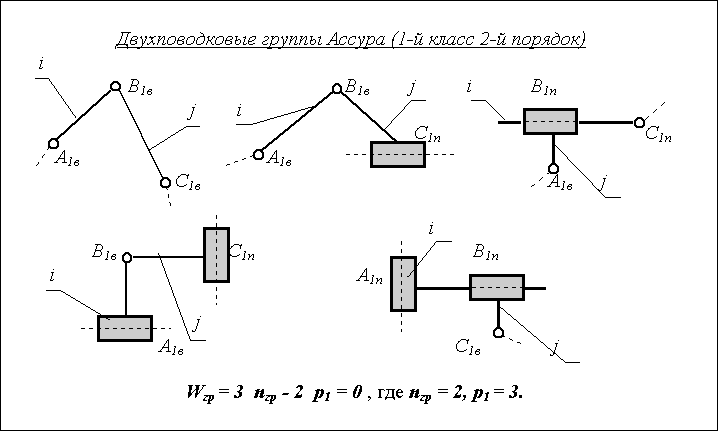
Рис. 1

Произвести структурный анализ механизма — это зна­чит определить число и вид кинематических пар; установить, из каких групп (первичного меха­низма и групп Ассура) состоит данный механизм и в какой последовательности эти группы присоединяются друг к другу; определить класс механизма. Класс механизма в целом определяется клас­сом самой сложной его структурной группы. Последовательность присоединения групп называется формулой строения механизма.

Рис. 2

При структурном анализе меха­низм расчленяется на отдель­ные структурные группы. Выделение из механизма групп Ассура нужно начинать с группы, наиболее удаленной от ведущего звена, с таким расчетом, чтобы при этом не на­рушалась связь с первичным механизмом.

Результаты структурного анализа механизма зависят в общем случае от того, какое из звеньев исследуемого ме­ханизма принято в качестве входного (ведущего).

Пример 1. Произвести структурный анализ механизма, представленного на рис. 2.

Решение. Механизм имеет пять подвижных звеньев. Названия звеньев: 1 — кривошип; 2 — шатун; 3 — коро­мысло; 4 — шатун; 5 — ползун. Стойка принята за нулевое звено. Звенья соединены между собой семью кинематическими парами V класса (на схеме они обозначены буквами латинского алфавита). Дан­ные о кинематических парах сводим в таблицу 1.

Таблица 1

обозначение КП	Шифр КП	номера звеньев, образующих КП	характер относительного движения звеньев КП	класс КП
O1	[1В]	0 и 1	вращательное	V
A	[1В]	1 и 2	вращательное	V
B	[1B]	2 и 3	вращательное	V
O2	[1B]	3 и 0	вращательное	V
D	[1B]	3 и 4	вращательное	V
E	[1B]	4 и 5	вращательное	V
F	[1П]	5 и 0	поступательное	V

Определяем подвижность механизма по формуле

где п = 5 — число подвижных звеньев; р₅ = 7 — число кинематических пар V класса; р₄ = 0 — число кинемати­ческих пар IV класса. Тогда

Это означает, что в данном механизме должно быть одно входное звено. В качестве входного звена принято звено 1 — кривошип.

Раскладываем механизм на структурные группы. Преж­де всего, отсоединяем группу Ассура, состоящую из звеньев 4 и 5 и трех кинемати­ческих пар: вращательных D и E и поступательной F (рис. 3, а). Степень подвижности этой группы после присоеди­нения к стойке:

Группа 4—5 является группой II класса II порядка.

а б

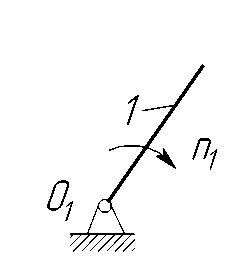
в

_{Рис. 3}

Затем отсоединяем группу, состоящую из звеньев 2 и 3 и трех вращательных пар А, В и О₂ (рис. 3, б). Степень подвижности этой группы после присоеди­нения к стойке:

Это группа II класса II порядка.

После отсоединения указанных групп остался первичный механизм, состоящий из кривошипа 1, присоединен­ного к стойке кинематической парой О₁ (рис. 3, в), и обладающий степенью подвижности

В целом рассматриваемый механизм является механиз­мом II класса. Формула строения механизма имеет вид:

ПМ (0;1)→ II (2;3) →II (4;5)