5.3. Тор

Функции параметрического описания поверхности тора запишем в следую­щем виде

где R u r — большой и малый радиусы, φ и ω — широта и долгота. Для замк­нутой поверхности углы φ и ω должны изменяться в полном круговом диапа­зоне, например, от 0 до 360° или от -180° до +180°.

На рис. 5.46, 5.47 показаны различные способы изображения тора.

Рис. 5.46. Простейшее изображение тора: а — каркас; б — поверхность с удаленными невидимыми точками

Рис. 5.47. Многогранники, диффузная модель отражения: а — обычное закрашивание; б — интерполяция по методу Гуро '

Рисование тора средствами компьютерной графики достаточно просто может быть выполнено на основе аппроксимации многогранником, подобно тому, что мы уже рассматривали для шара и цилиндра. Повторим запись алгоритма вывода многогранника четырехугольными гранями, видоизменив его для данного конкретного случая

Очевидно, что чем меньше величины dω и dφ, тем больше число граней у вписанного многогранника и тем лучше такой много­гранник соответствует гладкой поверхности тора. При использовании такого полигональ­ного метода получения изображения доста­точно просто наложить текстуру. Полиго­нальный способ наложения текстур для тора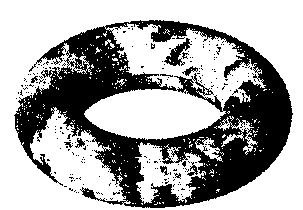

полностью аналогичен способу, рассмотрен- _ _ .„ _

„ ^{J v} * Рис. 5.48. Тор с текстурой

ному выше для шара. Пример подобного

текстурирования приведен на рис. 5.48.

Рассматривая в предыдущих разделах шар и цилиндр, мы наряду с полиго­нальными способами пытались анализировать и другие способы изображения. Например, рисование цилиндра вертикальными линиями. Для тора изо; брести эффективный специальный алгоритм графического вывода, вероятно достаточно сложно. Во всяком случае, автору он неизвестен. Хотя во второй части этой книги есть пример программирования одного "неполигонального¹! способа рисования тора. Можно представить тор как след движения шара, Если шар перемещается с достаточно малым шагом, то след получается весьма похожим на тор. Впрочем, данный пример рисования приведен в кни­ге не как рекомендуемый способ изображения тора, а как пример изображе­ния движущихся шариков. По быстродействию данный способ изображении тора весьма плох из-за того, что приходится многократно рисовать одни и те же точки (подобные аспекты мы рассматривали в главе 3 при обсуждении алгоритмов рисования толстых линий).

Вариации формы тора

На рис. 5.49 изображена поверхность многогранника, для которой парамет­рические формулы такие же, как и для тора. Единственное отличие здесь в том, что широта φ изменяется в диапазоне от -135° до +225° с шагом dφ =90°.

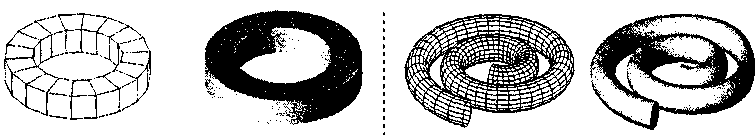
Рис. 5.49. Кольцо i Рис. 5.50. Спираль

Если изменять радиус R пропорционально долготе, т. е. R =R(ω), то полу­чим спираль (рис. 5.50). Здесь больший диапазон изменения долготы: от -360° до +360°, соответствует двум виткам спирали.

Для пружины (рис. 5.51) значения коорди­нат х и у такие же, как и для тора, а коор­дината z тора суммируется с приращением, пропорциональным долготе:

Рис. 5.51. Пружина

; где А: — некоторая константа, определяющая шаг витков спирали по высоте. Долгота здесь изменяется в троекратном круговом диапазоне (соответствую­щем числу витков).

Если объединить спираль и пружи­ну, то получим коническую спираль (рис. 5.52):

Рис. 5.52. Коническая спираль

где константа р определяет увеличение большого радиуса пропорционально долготе, а. к — задает шаг витков пружины по высоте.