4.2. Расчет валов и осей

Основные критерии работоспособности осей и валов - проч­ность и жесткость. В зависимости от характера напряжений, возни­кающих в валах и осях, возможны два случая их расчета на прочность: расчет на статическую прочность и расчет на усталостную прочность (выносливость).

Усталостная прочность оценивается коэффициентом запаса прочности. Неподвижные оси при действии постоянных нагрузок рас­считывают на статическую прочность. Подвижные быстроходные оси и валы рассчитывают на выносливость. Тихоходные валы и оси, на­груженные переменной нагрузкой, рассчитывают на статическую прочность и выносливость.

Расчет валов и осей на статическую прочность. Оси, нагруженные

только изгибающими нагрузками, рассчитывают на изгиб. После составления расчетной схемы и определения всех сил, дейст­вующих на ось, строят эпюру изгибающих моментов и по максималь­ному изгибающему моменту рассчитывают ось.

Расчет осей на статическую прочность при изгибе ведётся по формулам - проверочный (4.1), проектировочный (4.2):

, (4,1)

(4.2)

где - расчетное напряжение в опасном сечении оси; М - изги­бающий момент в опасном сечении оси; - момент сопротивле­ния изгибу сечения оси; d - диаметр оси; - допускаемое на­пряжение на изгиб.

Проектирование вала начинают с определения диаметра его вы­ходного конца из расчета на чистое кручение по пониженному допус­каемому напряжению, без учета влияния изгиба:

(4.3)

где T - крутящий момент, Н·мм; - допускаемое напряжение на кручение, для стальных валов = 20÷30 МПа.

Полученный результат округляют до ближайшего большего значения из стандартного ряда.

На основании расчетных схем валы рассчитывают на статиче­скую прочность при одновременном действии изгиба и кручения. Для этого силы, действующие на вал в разных плоскостях, раскладывают по двум взаимно перпендикулярным плоскостям и в этих плоскостях определяют опорные реакции и изгибающие моменты. Суммарный изгибающий момент равен:

где M_x и M_y - изгибающие моменты во взаимно перпендикулярных плоскостях в выбранном сечении вала.

Приведенный или эквивалентный момент вычисляют по третьей теории прочности:

(4.4)

Расчет вала на совместное действие изгиба и кручения ведётся по формулам - проверочный (4.5), проектировочный (4.6):

(4.5)

(4.6)

где - приведенное (эквивалентное) напряжение для расчетного сечения вала; d - диаметр вала; 0,1d³ - момент сопротивления сечения вала при изгибе; - допускаемое напряжение на изгиб, для стальных валов и осей с термической обработкой = 70÷80 МПа.

Проверочный расчет валов и осей на усталостную прочность.

Проверочный (уточненный) расчет выполняется, когда известна конструкция и размеры вала, расположение и виды концентраторов напряжений, опор и деталей, построены эпюры моментов и т.п. Расчет сводится к определению коэффициента безопасности в опасных сечениях вала по условию:

(4.7)

где S_σ - коэффициент безопасности по изгибу, определяемый как:

, - коэффициент безопасности по кручению, равный:

где σ_а и τ_а - переменные составляющие циклов изменения напряжений; σ_m и τ_m - постоянные составляющие циклов изменения напряжений; σ_-1 и τ_-1 - пределы выносливости при изгибе и кручении при симметричном знакопеременном цикле; ε_σ и ε_τ - масштабный фактор; К_σ и К_τ - эффективные коэффициенты напряжений при изгибе и кручении; - коэффициент, учитывающий влияние посадки деталей на вал при изгибе; - то же при кручении,

;

β коэффициент упрочнения, вводится для валов с поверхностным упрочнением; ψ_σ и ψ_τ- коэффициенты, характеризующие чувствительность материала к асимметрии цикла изменения напряжений.

Постоянные циклов изменения напряжения σ_m и τ_m (средние напряжения циклов) и переменные составляющие σ_а и τ_а (амплитуды) цикла определяют по зависимостям:

σ_m=0; σ_а=σ_F=

Если вал реверсируется, то:

τ_m=0;

Момент сопротивления вала W и полярный момент сопротивления Wp определяются по формулам:

для сплошного вала

W=0,ld³; W_p=0,2d³; W_p=2W;

для сечения вала со шпонкой

Расчет осей и валов на жесткость. Валы и оси, рассчитанные на статическую или усталостную прочность, не всегда обеспечивают нормальную работу машины. Под действием нагрузок валы и оси в процессе работы деформируются и получают линейные f и угловые θ перемещения (рис. 4.3), что, в свою очередь, ухудшает работоспо­собность отдельных узлов и машин. Так, например, значительный прогиб вала f вала электродвигателя, с одной стороны, уменьшает, а, с другой стороны, увеличивает зазор между ротором и статором, что отрицательно сказывается на его работе. Угловые перемещения θ ва­ла или оси ухудшают работу подшипников, точность зацепления пе­редач и т.п. Для обеспечения требуемой жесткости вала или оси необ­ходимо производить расчет на изгибную или крутильную жесткость.

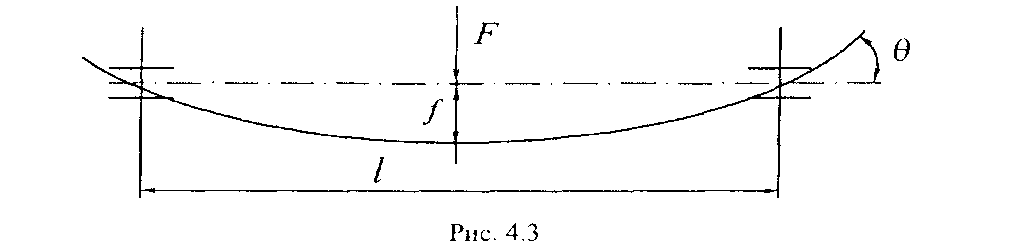
Для обеспечения жесткости на изгиб осей или вала необходимо, чтобы действительные значения θ и f не превышали допускаемых значений:

θ≤[θ], f ≤[f].

Для большинства валов жесткость на кручение не имеет суще­ственного значения, и такой расчет не производят. Расчет валов на крутильную жесткость производят для длинных валов. Оси на кру­тильную жесткость не рассчитывают.

Условия жесткости валов на кручение записывают, как:

,

где Т - крутящий момент в расчетном сечении, Нм; G - модуль сдвига (для стали G = 8·10⁴ H/мм2); I₀- полярный момент инерции

(для вала круглого сплошного сечения I₀ = 0,ld⁴).