Глава 3. Механические передачи движения

3.1. Общие сведения о передачах

Механизмы, служащие для передачи энергии с преобразованием скоростей, сил, моментов и видов движения, называются механическими передачами.

Механические передачи служат промежуточными звеньями в кинематической цепи от двигателя к исполнительным звеньям машины. Механические передачи используются для уменьшения скорости исполнительного звена, для повышения движущего момента на рабочем валу, для передачи движения от одного двигателя к нескольким исполнительным звеньям.

В зависимости от принципа действия различают механические передачи шарнирными соединениями, трением, зацеплением, гидравлические и пневматические.

К передачам шарнирно-рычажными соединениями относятся шарнирно-рычажные механизмы (шарнирный четырехзвенный, кривошипно-ползунный, кулисный, мальтийский, синусный, тангенсный и др.). К передачам трением относятся фрикционные и ременные; к передачам зацеплением - зубчатые, червячные, цепные и винт-гайка.

Основными характеристиками механических передач являются угловые скорости ведущего ω₁ и ведомого ω₂ валов; мощности на ведущем Р₁ и ведомом Р₂ валах. Дополнительными характеристиками являются: передаточное отношение i= ω₁/ω₂ – отношение угловой скорости ведущего вала к угловой скорости ведомого вала; окружная скорость V ведущего или ведомого звена; механический КПД - η; окружное усилие - F_t; крутящий момент - Т.

3.2. Передачи зацеплением

Основная теорема зацепления

Общая нормаль к сопряженным профилям в точке их касания делит расстояние между центрами вращения профилей на части, обратно пропорциональные угловым скоростям этих профилей.

Рассмотрим передачу вращения между валами с помощью двух взаимоогибающих профилей (1 и 2) (рис. 3.1).

Скорости профилей в точке их контакта (точка С) выражаются формулами:

v₁ =ω₁(О₁С); v₂ =ω₂(О₂С).

Для обеспечения непрерывной передачи движения необходимо, чтобы проекции этих скоростей на общую нормаль NN к профилям в точке их контакта были равны между собой, то есть

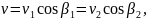
где и - углы между направлениями скоростей V₁ и V₂ и общей нормалью к профилям NN. Тогда имеем:

Принимая во внимание, что:

получаем:

или .

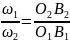ИЗ подобия треугольников 0₁B₁P₁ и 0₂В₂Р₂ следует:

Тогда - основная теорема зацепления.

На основании этой формулы можно записать выражение для пе­редаточного отношения:

Геометрическое место точек касания (точка С) двух сопряженных профилей на неподвижной плоскости называется линией зацепления.

Точка пересечения нормали NN с прямой 0₁0₂, являющаяся мгновенным центром вращения в относительном движении профилей, называется полюсом зацепления.

Основным условием правильной работы зубчатых передач является постоянство их передаточного отношения:

=const

Геометрическое место последовательных положений точки Р на плоскостях, связанных с профилями 1 и 2 (см. рис. 3.1), называют центроидами относительного движения.

При постоянном передаточном отношении центроиды представляют собой окружности, которые называются начальными.

Зубчатые механизмы (передачи)

Среди механических передач зацеплением наиболее распространены зубчатые. Простая зубчатая передача представляет собой трехзвенный механизм с одной высшей кинематической парой. Если число звеньев передачи больше трех, то ее называют сложной.

Зубчатые передачи (рис. 3.2) преобразуют вращение ведущего зубчатого колеса во вращение ведомого колеса путем нажатия зубьев первого на зубья второго. Меньшее зубчатое колесо передачи называется шестерней, большее - колесом.

Зубчатые передачи могут преобразовывать вращательное движение между валами с параллельными (рис. 3.2, а ,б, в, ж), пересекающимися (рис. 3.2, г, д) и перекрещивающимися (рис. 3.2,е) осями.

Формы зубчатых колес и формы зубьев передачи бывают: цилиндрические - прямозубые (рис. 3.2, а ,з), косозубые (рис. 3.2, б) и шевронные (рис. 3.2, в); конические - прямозубые (рис. 3.2, г), косозубые (рис. 3.2, д) и с круговыми зубьями; винтовые (рис. 3.2, ж), состоящие из двух цилиндрических косозубых колес, установленных на пересекающихся валах.

В зависимости от взаимного расположения зубчатых колес различают зубчатые передачи с внешним (рис. 3.2, а) и внутренним зацеплением (рис. 3.2, ж).

К зубчатым передачам относится реечная передача (рис. 3.2, и), преобразующая вращательное движение шестерни в возвратно-поступательное движение рейки или наоборот. Зубчатые передачи в различных сочетаниях образуют многоступенчатые зубчатые передачи, а также могут быть выполнены в виде планетарных и волновых передач. Наиболее распространены цилиндрические и конические зубчатые передачи.

Цилиндрические передачи с прямозубыми колесами просты в изготовлении, не имеют осевых нагрузок, но по сравнению с другими видами колес имеют меньшую грузоподъемность и шумны при работе.

Косозубые колеса по сравнению с прямозубыми имеют большую грузоподъемность, отличаются плавностью и бесшумностью работы, но возникающие осевые силы дают дополнительные нагрузки на опоры. Шевронные передачи отличаются большой грузоподъемностью, плавностью и бесшумностью работы, но сложны в изготовлении.

Зубчатые передачи нашли самое широкое применение благодаря компактности, высокому КПД, постоянству передаточного числа, большой долговечности и надежности в работе.

Передаточное отношение пары зубчатых колес (одноступенчатая передача) определяется по формуле:

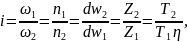
где ω₁, n₁, dw₁, Z₁ и Т₁ - соответственно угловая скорость, частота вращения, начальный диаметр, число зубьев и крутящий момент ведущего колеса; ω₂, n₂, dw₂, Z₂ и Т₂ - то же, ведомого зубчатого колеса; η - КПД передачи.

Отношение числа зубьев Z₂ колеса к числу зубьев Z₁ шестерни называется передаточным числом зубчатой передачи и, т.е. и = .

Если ведущим зубчатым колесом является шестерня, то для такой передачи передаточное отношение и передаточное число представляют собой одну и ту же величину.

По форме профиля зуба наиболее распространен эвольвентный, предложенный Эйлером в 1760 г. Круговой профиль зуба предложен М.Л.Новиковым. По сравнению с эвольвентным он позволяет повысить нагрузочную способность зубчатых передач. Она примерно в 1,5 - l,7 раза больше, чем у аналогичной по размерам и материалу эвольвентной косозубой передачи. Исполнение зубчатого зацепления с круговым профилем зубьев (рис. 3.3) может быть в прямозубом и косозубом вариантах. С зацеплением Новикова изготавливают передачи не только цилиндрические, но и конические.

Планетарными и дифференциальными называют зубчатые передачи, имеющие зубчатые колёса с перемещающимися осями (рис. 3.4). Движение этих колёс (планетарное) подобно движению планет, отчего планетарные передачи и получили своё название. Зубчатые колёса 1, З, с которыми сцепляются сателлиты 2, называются центральными. Оси сателлитов закреплены в водиле Н и вращаются вместе с ним вокруг центральной оси.

В планетарных передачах одно из центральных колес установлено неподвижно, степень подвижности такого механизма равна единице.

Ведущим (или ведомым) валом передачи служит вал подвижного центрального колеса, а ведомым (или ведущим) - вал водила. Если вращаются все зубчатые колёса и водило, то механизм называется дифференциальным (рис. 3.4, 6). В таком механизме два основных звена ведущие (или ведомые), а третье - ведомое (или ведущее); степень подвижности дифференциальных механизмов равна двум и более.

Для кинематического расчета дифференциальных механизмов используется формула Виллиса:

(3.1)

для механизма, изображенного на рис. 3.4, б, она имеет вид:

где и - передаточные отношения от колеса к последующему

колесу n или 3 простого ряда при неподвижном водили Н; или n₁ ,n_з, n_н - угловые скорости и частоты вращения звеньев валов колёс 1, 3, n и водила Н.

Передаточное отношение может быть выражено через числа зубьев с учетом направления их вращения в простом ряду. При внешнем зацеплении пары колес ее передаточное отношение приобретает знак минус (колёса вращаются в разные стороны), при внутреннем зацеплении пары колёс и передаточное отношение имеет знак плюс (вращение колес совершается в одну сторону). Применительно к схеме на рис. 3.4, б:

Так как данный дифференциальный механизм имеет две степени свободы W = 3n - 2 p₅ - р₄ = 3∙4 – 2∙4 - 2 = 2; где n = 4 – число подвижных звеньев, p₅ = 4 - число кинематических пар 5-го класса; р₄ = 2 - число кинематических пар 4-го класса), то для получения полной определённости движения всех звеньев необходимо задавать законы движения двум его звеньям из трех (ω₁, ω₃, ω_i). Третья неизвестная величина определится по формуле Виллиса (3.1).

Зависимость между угловыми скоростями (частота вращения) звеньев планетарного механизма определяется по формуле (3.1), в ко­торой скорость неподвижного центрального колеса приравнивается к нулю:

(3.2)

Передаточные отношения от первого колеса к водилу при неподвижном колесе 3 на основании формулы (3.2) равны:

Таким образом, по формуле Виллиса определяется передаточное число для любой схемы планетарного и дифференциального механизмов.

Основное достоинство планетарных передач - большие передаточные отношения, компактность и малая масса. С помощью дифференциальных передач в машинах получается сложение или разложение движения. Планетарные передачи, благодаря своим достоинствам, нашли широкое применение в станкостроении, транспортном машиностроении, приборостроении. Однако планетарные передачи сложны в сборке, требуют повышенной точности изготовления, кроме того, при очень больших передаточных отношениях ухудшается работа планетарной передачи и ее КПД получается низким.

Волновые зубчатые передачи основаны на принципе преобразования параметров движения за счет волнового деформирования одного из звеньев (колеса) механизма. Наиболее распространённая волновая зубчатая передача (рис. 3.5) состоит из водила Н с двумя роликами, свободно вращающимися на осях, закрепленных в водиле (генератор волн), неподвижного жесткого зубчатого колеса 1 с внутренними зубьями и вращающегося гибкого колеса 2 с наружными зубьями.

Вращательное движение в волновой зубчатой передаче осуществляется от ведущего звена к ведомому благодаря бегущей волновой деформации гибкого зубчатого колеса. При вращении водила деформация гибкого зубчатого колеса перемещается по окружности, охватывающей водило, в виде бегущей волны. Поэтому передача называется волновой, а водило - волновым генератором. Ведущим звеном в волновой зубчатой передаче может быть водило или любое зубчатое колесо.

Разность чисел зубьев волновой передачи принимается равной или кратной числу волн К:

z₁-z₂= К,

где z₁ и z₂, соответственно, число зубьев жесткого и гибкого зубчатых колёс.

Так, в волновой передаче с генератором с двумя роликами образуются две волны - передача называется двухволновой. При трех роликах, расположенных под углом 120°, получают трехволновую передачу.

Если ведущим звеном гибкой передачи служит волновой генератор, а ведомым - гибкое колесо. то передаточное отношение такой передачи имеет вид:

где ω_Н и n_Н - угловая скорость и частота вращения волнового генератора; ω₂ и n₂ - угловая скорость и частота вращения гибкого зубчатого колеса. δ= d₁- d₂ - разность между делительными диаметрами жесткого колеса d₁ и меньшим делительным диаметром гибкого зубчатого колеса d₂.

Волновая зубчатая передача может осуществлять большие передаточные отношения (i ≥1000), а также передавать большие нагрузки. Достоинством гибкой зубчатой передачи является также возможность передачи движения в герметизированное пространство. Недостатки волновых передач: сложность конструкции, пониженные надежность и долговечность гибкого зубчатого колеса, повышенные потери мощности на трение в передаче и на деформацию гибкого зубчатого колеса.

Червячные передачи (рис. 3.2, е, з). Червячная передача состоит из винта, называемого червяком, и червячного колеса, представляющего собой разновидность косозубого колеса. Резьба червяка может быть однозаходной или многозаходной. Наиболее распространена правая резьба с числом захода z₁= 1 .. .4.

Различают два основных вида червячных передач: цилиндрические (с цилиндрическими червяками) и глобоидные (с глобоидными червяками в осевом сечении, имеющими обычно трапецеидальный профиль резьбы).

Достоинства червячной передачи: большие передаточные числа, плавность и бесшумность работы. Недостатки: низкий КПД, сильный нагрев, повышенный износ и дороговизна.

Передаточное отношение червячной передачи имеет вид:

где ω₁, ω₂ - угловые скорости червяка и колеса; Т₂ и Т₁ - крутящие моменты, передаваемые соответственно червячным колесом и червяком; γ_ω - начальный угол подъема резьбы червяка; η – КПД передач.

Если ведущее звено - червяк, то передаточное отношение i и передаточное число и имеют одинаковое значение:

где Z₂ - число зубьев колеса; Z₁ - число заходов червяка.

Передаточное число червячной передачи принимают в пределах и = 8 ... 90, но в специальных установках оно должно доходить до и = 1000 и более.

Цепные передачи (рис. 3.б, а) представляют собой ведущую и ведомую звездочки и цепь, охватывающую эти звездочки. Передачи раз­деляют на:

1. Грузовые, работающие при больших нагрузках и малых (или равных нулю) скоростях, для подъема и опускания грузов. Здесь ис­пользуют круглозвенные или простые пластинчатые цепи (рис. 3.б, 6,6).

2. Тяговые, работающие при средних скоростях (до 4 м/с), для перемещения груза в транспортирующих машинах. Здесь используют цепи из простых пластин и осей со втулками (или без них), рис. 3.б, г.

3. Приводные, работающие при значительных скоростях, передавая механическую энергию от ведущего вала к ведомому. Здесь используют втулочные, роликовые, крючковые, зубчатые цепи (рис. 3.б, д).

Применение многорядных цепей в передачах позволяет увеличить нагрузку пропорционально числу рядов.

Достоинствами цепных передач являются: постоянное передаточное отношение, высокий КПД, передача движения на большие расстояния, возможность передачи движения от одной ведущей звездочки нескольким ведомым.

Недостатками цепных передач являются: необходимость высокой точности изготовления, наличие натяжного устройства (при вытягивании цепи), необходимость смазки и регулировки.

Передаточное отношение цепной передачи

где z₁, n₂, z₂, n₁ - соответственно числа зубьев и частоты вращения ведущей и ведомой звездочек.