Введение

Учебная дисциплина «Механика» состоит из трех разделов: «Теоретическая механика», «Сопротивление материалов» и «Детали машин».

В данном учебном пособии компактно и в доступной форме излагаются курсы теоретической механики, сопротивления материалов и деталей машин. Объем представленного материала соответствует Примерной программе дисциплины «Механика» для групп специальностей с объемом 200 учебных часов. Для групп с меньшим объемом часов можно выбрать необходимый материал с программами дисциплины для запланированного количества учебных часов и примерного уровня требований.

Данное пособие будет особенно полезно при самостоятельной работе над курсом студентам, изучающим данный раздел механики, где согласно учебным планам выделяется только один семестр.

Раздел I. Теоретическая механика.

Часть 1. Статика.

Теоретическая механика – это наука, в которой изучаются общие законы механического движения и механического взаимодействия материальных тел.

Механическим движением называется перемещение одного тела по отношению к другому, происходящее в пространстве и во времени.

Механическим взаимодействием называется такое взаимодействие материальных тел, которое изменяет или стремится изменить характер их механического движения.

Статика – это раздел механики, в котором изучаются методы преобразования систем сил в эквивалентные системы и устанавливаются условия равновесия сил, приложенных к твердому телу.

Основные понятия и определения,

Материальное тело, размеры которого в рассматриваемых конкретных условиях можно не учитывать, называется материальной точкой.

Материальная точка обладает массой и способностью взаимодействовать с другими телами.

Системой материальных точек называется такая совокупность материальных точек, в которой положение и движение каждой точки зависят от положения и движения других точек этой системы.

В теоретической механике часто рассматривают тела, расстояние между любыми точками которых, остаются неизменными. Такие тела называются абсолютно твердыми. Понятие об абсолютно твердом теле – есть абстрактная модель. Принимая эту модель в качестве объекта исследования, пренебрегают возможными изменениями формы и размеров тела под действием нагрузок: считая, что

1. деформации малы – ими можно пренебречь;

2. условия равновесия сил, приложенных к абсолютно твердому телу являются необходимыми условиями равновесия любого деформируемого тела.

Важнейшим понятием в теоретической механике является понятие силы.

Сила – это мера механического взаимодействия тел, определяющая интенсивность и направление этого взаимодействия.

Сила определяется тремя элементами: числовым значением, направлением и точкой приложения. Сила изображается вектором ( ) За единицу силы принимается Ньютон ( ). Прямая, по которой направлена сила называется линией действия силы.

Совокупность нескольких сил, действующих на данное тело называется системой сил

( )

Если, не нарушая состояния тела, одну систему сил ( ) можно заменить другой системой ( ) и наоборот, то такие системы сил называются эквивалентными

( )  ( ).

В том случае, когда система сил ( ) эквивалентна одной силе , то есть ( )  , то последняя называется равнодействующей этой системы сил.

Если абсолютно твердое тело остается в состоянии покоя при действии на него системы сил ( ), то последняя называется уравновешенной системой сил или системой сил эквивалентной нулю

( )  0.

Часто в этом случае говорят, что тело находится в равновесии.

Силы, действующие на материальную систему делятся на 2 группы: внешние и внутренние.

Внешними называются силы, действующие на материальные точки данной системы со стороны материальных точек, не при­надлежащих этой системе. (обозначаем – ).

Внутренними называются силы взаимодействия между материальными точками рассматриваемой системы. (обозначаем - ),

Аксиомы статики.

Аксиома 1.

Две силы, приложенные к абсолютно твердому телу, будут уравновешены тогда и только тогда, когда они равны по модулю, действуют по одной прямой и направлены в противоположные стороны.

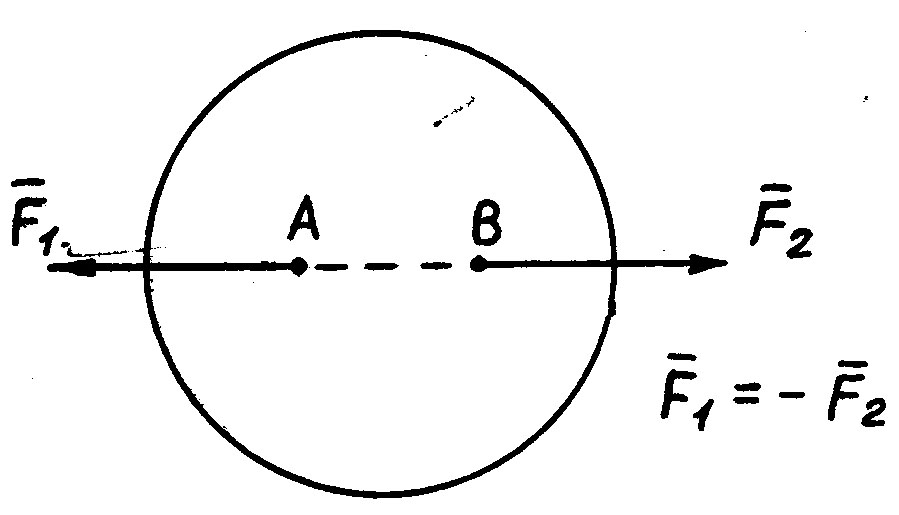
Аксиома 2.

Не нарушая состояния абсолютно твердого тела, к нему можно прикладывать или отбрасывать силы тогда и только тогда, когда они составляют уравновешенную систему. Следствие. Не нарушая состояния тела, точку приложения силы можно переносить вдоль ее линии действия (сила - вектор скользящий).

Доказательство

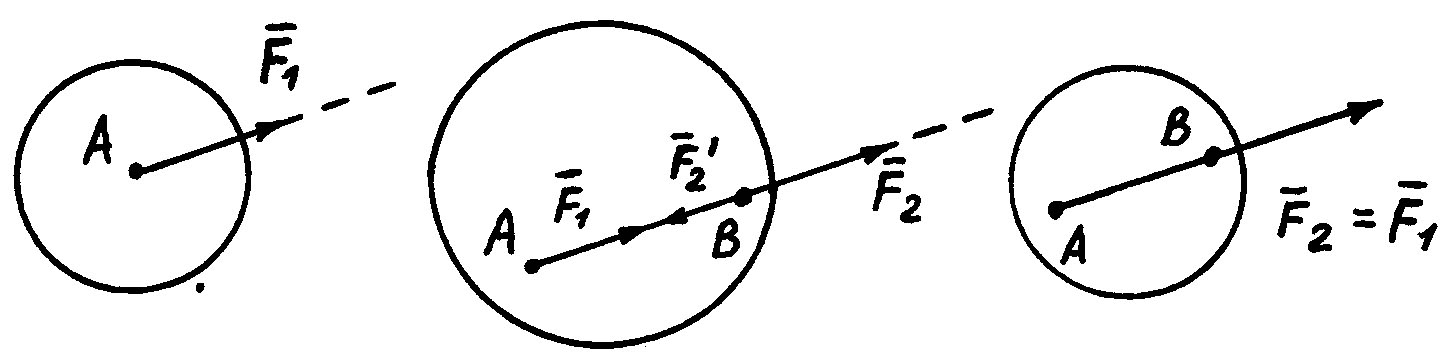
Пусть сила приложена в точке А. Приложим в точке В, на линии действия силы две уравновешенные силы  0, полагая, что .

Согласно аксиоме 2

 ,

но система  0 и следовательно, её можно отбросить, т.е.  , что и требовалось доказать. В результате на тело будет действовать только одна сила , но приложенная в точке В.

Аксиома 3.

He меняя состояния тела, две силы, приложенные к одной его точке можно заменить одной равнодействующей силой, приложенной в той же точке и равной их геометрической сумме

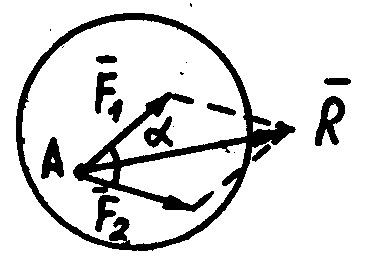
1)

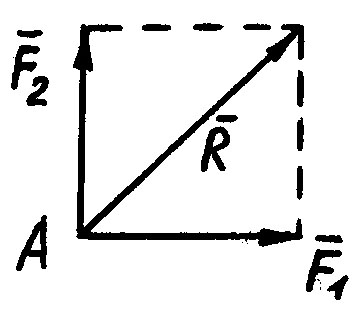
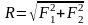
2)

3)

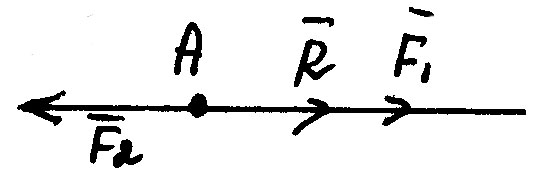
Аксиома 4.

Силы взаимодействия двух тел равны по модулю и направлены по одной прямой в противоположные стороны.

Аксиома 5.

Равновесие деформируемого тела на нарушится, если жестко связать его точки и считать тело абсолютно твердым.

Связи. Реакции связей.

Тело называется свободным, если его перемещения в пространстве ничем не ограничены. Тело, перемещения которого ограничены другими телами, называется несвободным, а тела, ограничивающие перемещения данного тела, называются связями. В точках контакта возникают силы взаимодействия между данным телом и связями. Силы, с которыми связи действуют на данное тело, называются реакциями связей.

Одним из основных положений механики является принцип освобождаемости твердых тел от связей, согласно которым всякое несвободное тело можно рассматривать как свободное, если действие связей заменить реакциями их, приложенными к данному телу.

Реакция любой связи направлена противоположно тому направлению, в котором связь ограничивает перемещение тела.

Основные виды связей.

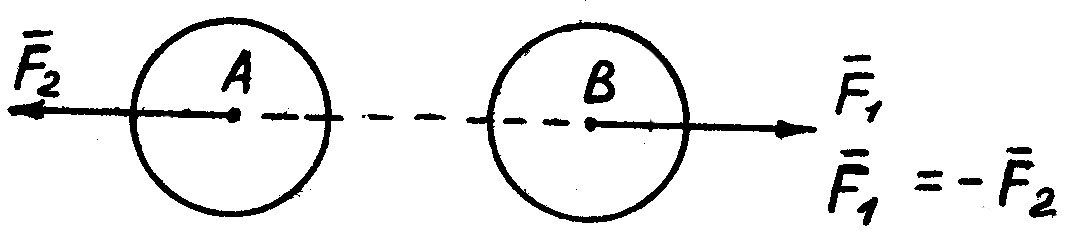
1) Идеально гладкая поверхность.

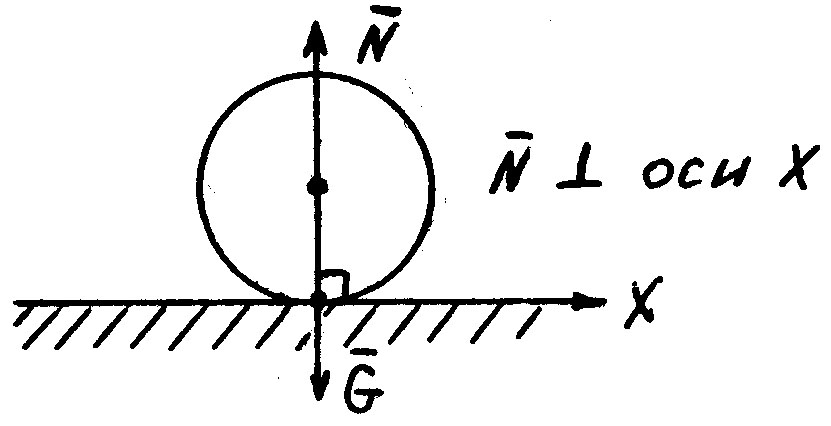
2) Гибкая связь (трос, нить, цепь, канат).

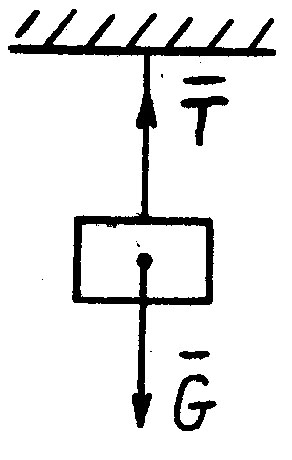
Реакция гибкой связи направлена по нити к точке подвеса.

3)

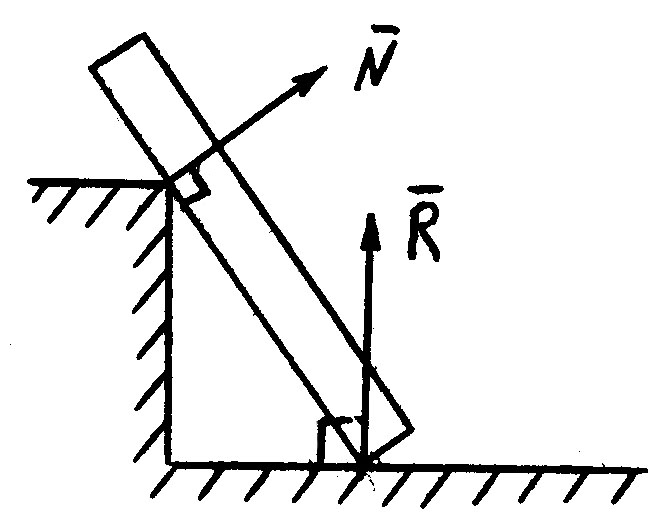
Твёрдое тело имеет гладкую поверхность и опирается на остриё или упирается остриём.

4) Цилиндрическая шарнирно-неподвижная опора (подшипник).

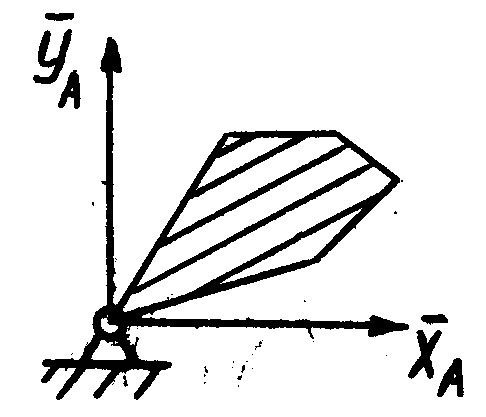
Реакция такой опоры имеет произвольное направление в плоскости, раскладываем её на две составляющие .

5) Цилиндрическая шарнирно-подвижная опора.

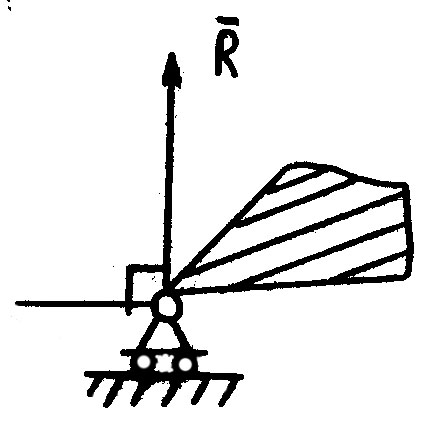
6) Невесомый стержень, на концах которого шарниры.

7) Сферический шарнир.

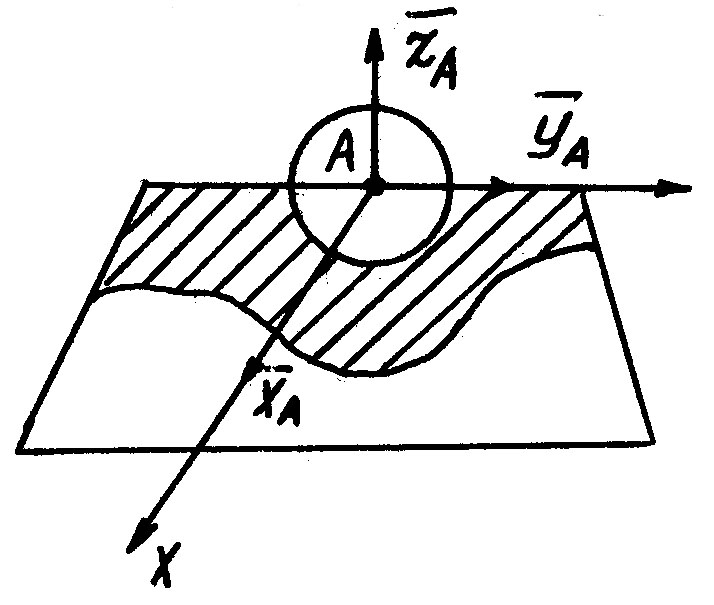
Шар, который может вращаться как угодно внутри сферической полости. Центр шара остается неподвижной точкой, через которую проходит линия действия реакции. Реакция имеет произвольное направление в пространстве, раскладываем ее на 3 взаимно-перпендикулярных составляющих .

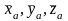8) Подпятник.

Реакция имеет произвольное направление в пространстве, раскладываем ее на три взаимно-перпендикулярных составляющих

Заделка.

Заделка – особый вид связи, препятствующий не только линейным перемещениям закрепленной точки тела, но и повороту вокруг этой точки.

Рассмотрим жесткую заделку левого конца балки АВ.

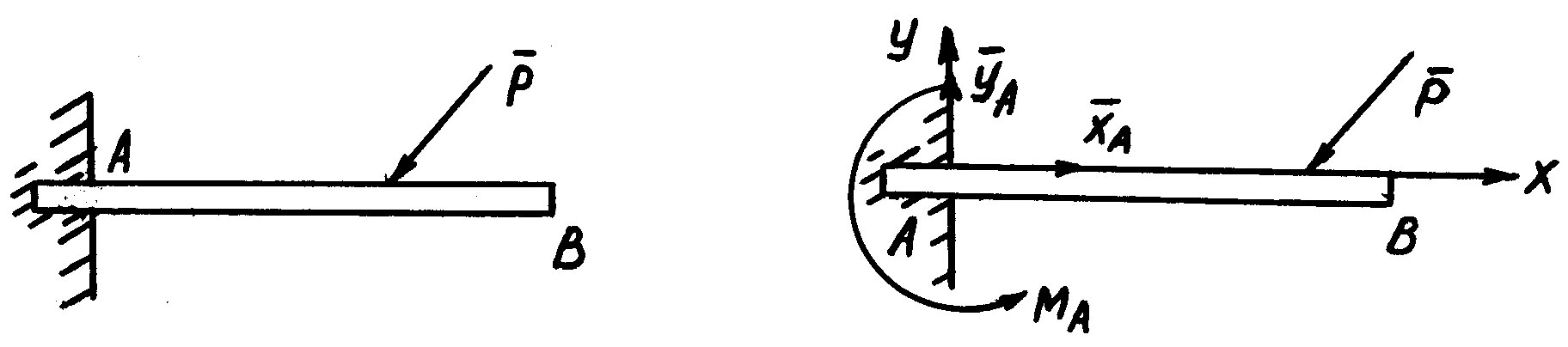
Этот конец оказывается полностью закрепленным – не возможны его вертикальное и горизонтальное перемещения, а также и поворот. Такая связь создает систему реакций, состоящую из двух составляющих и пары, момент которой обозначен через .

Это следует из того, что на заделанный конец балки действует распределенная нагрузка, которую можно привести к силе, приложенной в точке А, и паре сил с моментом .

Следовательно, реакция заделки складывается из двух взаимно перпендикулярных составляющих и пары, момент которой подлежит определению.

Система сходящихся сил.

Сходящимися называются силы, линии действия которых пересекаются в одной точке. Система сходящихся сил эквивалентна одной силе, равнодействующей, которая равна геометрической сумме этих сил и проходит через точку пересечения их линией действия.

Доказательство:

Пусть задана система сходящихся сил , приложенных к абсолютно твердому телу. Согласно следствию из аксиомы 2 перенесем точки приложения сил по линиям их действия в точку пересечения этих линий. Получаем систему сил, приложенных в одной точке. Она эквивалентна исходной системе сходящихся сил.

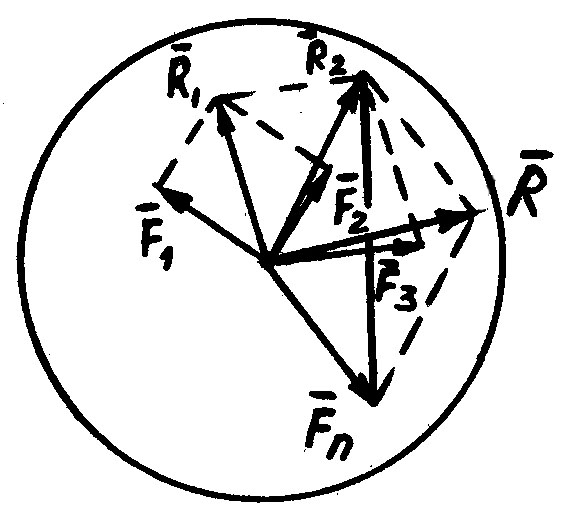
(1)

Геометрический способ построения равнодействующей.

Строим силовой многоугольник: от конца отложим от его конца и так далее. Затем соединим начало первого вектора с концом последнего. Полученный вектор и есть .

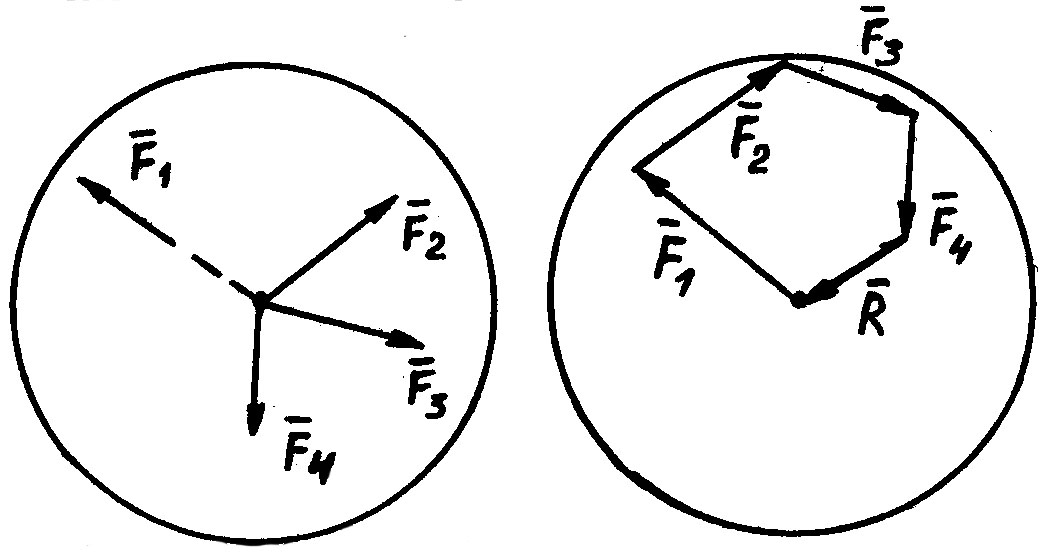
Обе части (1) спроектируем на оси .

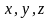(2)

Модуль равнодействующей (3)

Направление равнодействующей определяется направляющими косинусами.

– единичные орты осей соответственно.

Условия равновесия системы сходящихся сил

При приведении системы сходящихся сил к центру было показано, что такая система эквивалентна одной равнодействующей .

Из определения уравновешенной системы сил следует, что для равновесия тела, находящегося под действием системы сходящихся сил, необходимо и достаточно, чтобы .

Это означает, что в силовом многоугольнике уравновешенной системы сходящихся сил конец последней силы должен совпадать с началом первой, то есть многоугольник замкнут. Равенство (*) на основании (3) с учетом (2) выполняется при условии, что

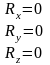или (4)

Для равновесия системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекции всех сил данной системы на координатные оси равнялись нулю.

Для плоской системы сходящихся сил система (4) принимает вид:

(5)

Теорема о 3-х непараллельных силах

Если тело находится в равновесии вод действием 3-х непараллельных сил и линии действия двух сил пересекаются, то все силы лежат в одной плоскости и их линии действия пересекаются в одной точке.

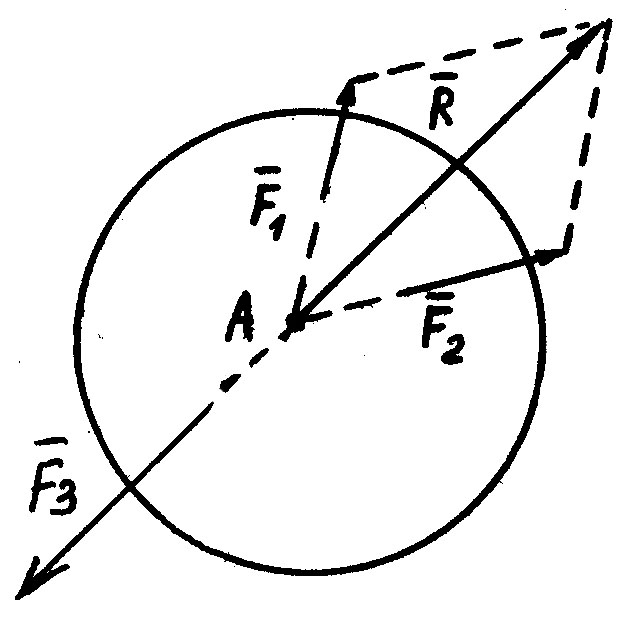
Доказательство:

Пусть на тело действует система трех сил , причем линии действия сил пересекаются в точке А. Согласно аксиоме 3 их можно заменить одной силой .

Таким образом, рассматриваемая система сил приведена к двум силам и . По условиям теоремы тело находится в равновесии, следовательно, по аксиоме 1 силы и должны иметь общую линию действия, но тогда линии действия всех трех сил должны пересекаться в одной точке.