2. Примеры решения задач.

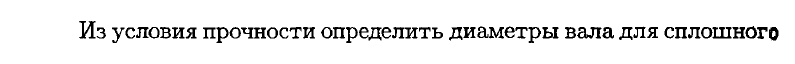
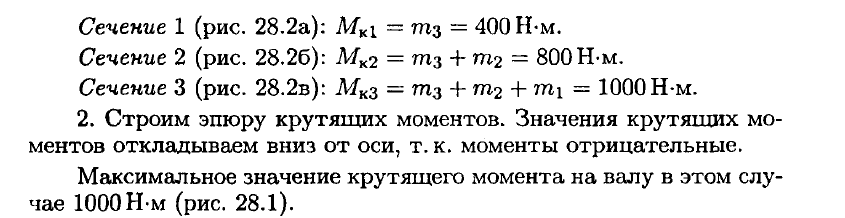
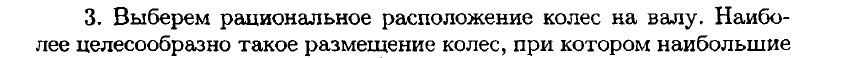
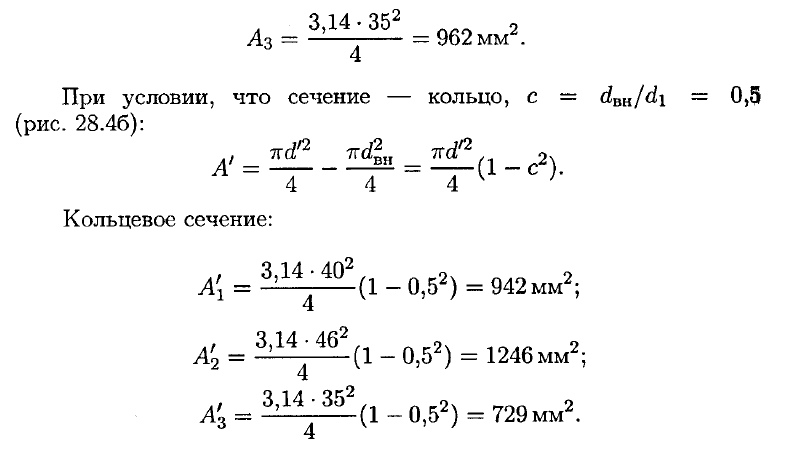
Пример 3.

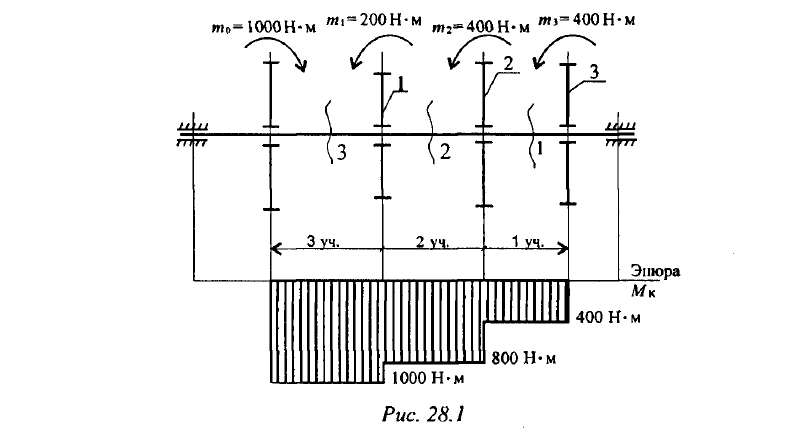
Жестко закрепленный на одном торце стальной вал сплошного ступенчато-постоянного сечения находится под действием пока­занныx на рис. 4.9, а скручивающих нагрузок.

Требуется построить эпюру крутящих моментов и определить значения наибольших касательных напряжений на каждом участке вала и углы поворота характерных сечений. В расчетах принять модуль упругости при сдвиге G = 0,8*10⁵ М Па = 0,8 . 10⁴ кН/см².

Вычисляем значения крутящих моментов в характерных сечениях вала, начиная со свободного конца.

1. Сечение х=2м, М_к =О.

2. Сечение х= 1 м (справа), M_к =-100*1 =-100 Нм.

3. Сечение х = 1 м (слева), М_К = - 100 + 400 = 300 Нм.

4. Сечение х = 0, М_К = 300 Нм.

Эпюра крутящих моментов приведена на рис. 4.9, б. На первом участке крутящий момент имеет постоянное значение, а на втором участке он изменяется по линейному закону. В сечении, соответ­ствующем границе участков, крутящий момент имеет скачок на величину сосредоточенного момента 400 Нм.

Вычисляем значения наибольших касательных напряжений на каждом участке вала и углы закручивания участков.

Первый участок (D₁ = 4 см).

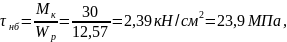
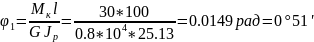
Второй участок (D₂ = З см).

Угол закручивания второго участка вала вычислен с помощью площади эпюры крутящих моментов.

Определяем угол поворота правого торцевого сечения вала:

Торцевое сечение поворачивается по ходу часовой стрелки.

Эпюра углов закручивания вала показана на рис. 4.9, в. На первом участке углы закручивания изменяются по линейному закону, а на втором -- по квадратичному закону.

Глава 4. Геометрические характеристики плоских сечений

1. Основные понятия

При растяжении (сжатии) мы встречались с простейшей геометрической характеристикой поперечного сечения — площадью . При изгибе и кручении этой характеристики недостаточно.

Возьмем, к примеру, брус прямоугольного поперечного сечения с площадью , приложим к свободному концу силу (рис. 4.1)

Рис. 4.1

Расположим его сечение по отношению к нагрузке как показано на рис. 4.1,а,б. В зависимости от ориентации сечения прогибы будут разными.

Вывод: площадь поперечного сечения не может характеризовать сопротивляемость стержня изгибу. Необходимо привлекать к рассмотрению более сложные геометрические характеристики.

2. Статические моменты сечения

Возьмем некоторое поперечное сечение бруса (рис. 4.2)

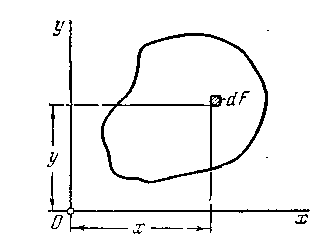
Рис. 4.2

Свяжем его с системой координат и рассмотрим два следующих интеграла

(4.1)

Индекс у интеграла означает, что интегрирование ведется по всей площади сечения.

Первый интеграл называется статическим моментом сечения относительно оси , а второй статическим моментом относительно оси . Размерность — .

При параллельном переносе осей величины статических моментов меняются. Рассмотрим две пары параллельных осей и (рис. 4.3).

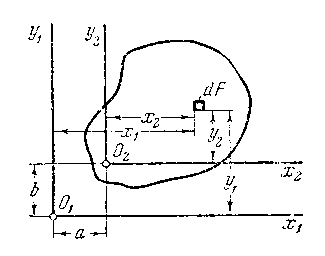
Рис. 4.3

Пусть расстояние между осями и равно , а между 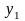и равно . Дано: 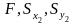. Требуется определить .

Очевидно, что

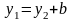
Искомые статические моменты равны

Или .

Рассмотрим подробнее, например, первое из полученных выражений

Величина может быть как положительной, так и отрицательной. Всегда можно подобрать так, причем единственным образом, чтобы,

, тогда . Ось, относительно которой статический момент равен “0”, называется центральной.

Расстояние до центральной оси от некоторой произвольной равно

, (4.2)

аналогично

. (4.3)

Таким образом, с помощью формул (4.2), (4.3) можно найти центр тяжести любой фигуры.