
- •Учебно-методическое пособие
- •Введение
- •Индивидуальная работа №1 Элементы комбинаторики. Основные понятия и теоремы теории вероятностей.
- •1. Основные формулы комбинаторики
- •Решение. Искомое число способов .
- •Общее число вариантов отбора равно .
- •Индивидуальная работа №2 Повторные независимые испытания
- •Индивидуальная работа №3 Непрерывная случайная величина
- •Задача 1
- •Задача 2
- •Задача 3
- •Индивидуальная работа №4 Основные законы распределения случайной величины. Закон больших чисел
- •1. Закон нормального распределения
- •2. Задачи на распределение Пуассона и показательное распределение
- •Индивидуальная работа №5 Случайные процессы. Цепи Маркова
- •Индивидуальная работа №6 Выборочный метод
- •1. Собственно – случайный отбор
- •2. Типический отбор
- •Индивидуальная работа №6 Статистическая проверка гипотез Сравнение двух дисперсий нормальных генеральных совокупностей
- •Используется критерий т распределения Стьюдента. При этом
- •Выбор знака неравенства в альтернативной гипотезе.
- •Индивидуальная работа №8 Корреляционный анализ
- •Рекомендуемая литература
- •Критические точки распределения
Индивидуальная работа №5 Случайные процессы. Цепи Маркова
1.
Состояние курса акций имеет 3 фазы:
![]() – низкий уровень,
– низкий уровень,
![]() – средний уровень,
– средний уровень,
![]() – высокий уровень. Вектор начального
состояния курса
– высокий уровень. Вектор начального
состояния курса
![]() в начале первого года приведен в таблице
1.
в начале первого года приведен в таблице
1.
Таблица 1
№ варианта |
|
|
|
1 |
2 |
3 |
4 |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
0,2 0,1 0,3 0,1 0,4 0,2 0,3 0,2 0,7 0,3 0,1 0,5 0,2 0,1 0,3 0,3 0,1 0,4 0,8 0,2 0,4 0,1 0,7 0,3 0,5 |
0,5 0,8 0,6 0,2 0,5 0,2 0,2 0,4 0,1 0,4 0,6 0,1 0,6 0,7 0,3 0,5 0,3 0,4 0,1 0,3 0,3 0,5 0,2 0,6 0,4 |
0,3 0,1 0,1 0,7 0,1 0,6 0,5 0,4 0,2 0,3 0,3 0,4 0,2 0,2 0,4 0,2 0,6 0,2 0,1 0,5 0,3 0,4 0,1 0,1 0,1 |
26 27 28 29 30 |
0,6 0,2 0,5 0,1 0,6 |
0,2 0,7 0,3 0,4 0,3 |
0,2 0,1 0,2 0,5 0,1 |
В таблице 2 даны частоты перехода трех состояний курса акций.
Таблица 2
№ варианта |
От состояния |
К состоянию |
Сумма по строке |
||
низкий |
нормальный |
высокий |
|||
1 |
2 |
3 |
4 |
5 |
6 |
1 |
|
15 10 0 |
5 75 12 |
0 15 18 |
20 100 30 |
2 |
|
27 32 0 |
18 64 10 |
9 32 30 |
54 128 40 |
3 |
|
42 30 6 |
14 90 24 |
0 15 54 |
56 135 84 |
4 |
|
43 16 5 |
7 80 15 |
0 24 35 |
50 120 55 |
5 |
|
20 13 0 |
12 78 9 |
4 26 36 |
36 117 45 |
6 |
|
18 22 0 |
6 66 15 |
0 33 30 |
24 121 45 |
7 |
|
15 7 0 |
10 84 12 |
0 21 24 |
25 112 36 |
8 |
|
21 32 4 |
14 96 12 |
7 16 24
|
42 144 40 |
9 |
|
33 15 6 |
11 90 18 |
0 30 30 |
44 135 54 |
10 |
|
28 26 0 |
14 91 18 |
0 13 45 |
42 130 63 |
11 |
|
25 17 0 |
15 136 8 |
5 51 22 |
45 204 30 |
Продолжение таблицы 2 |
|||||
1 |
2 |
3 |
4 |
5 |
6 |
12 |
|
27 26 0 |
15 91 5 |
6 39 30 |
48 156 35 |
13 |
|
16 12 6 |
14 71 12 |
0 17 18 |
30 100 36 |
14 |
|
27 24 0 |
9 84 12 |
0 36 27 |
36 144 39 |
15 |
|
20 55 30 |
16 77 10 |
0 11 5 |
36 143 45 |
16 |
|
26 18 0 |
13 162 10 |
0 18 14 |
39 198 24 |
17 |
|
21 30 0 |
6 165 20 |
3 15 32 |
30 210 52 |
18 |
|
8 28 3 |
4 63 12 |
2 14 18 |
14 105 33 |
19 |
|
36 13 0 |
18 104 25 |
6 39 30 |
60 156 55 |
20 |
|
27 34 4 |
6 170 8 |
0 17 10 |
33 221 22 |
21 |
|
18 18 0 |
15 144 14 |
0 36 35 |
33 198 49 |
22 |
|
16 33 6 |
6 110 9 |
0 22 18 |
22 165 33 |
23 |
|
21 45 5 |
18 120 15 |
0 30 35 |
39 195 55 |
Продолжение таблицы 2 |
|||||
1 |
2 |
3 |
4 |
5 |
6 |
24 |
|
18 26 0 |
8 78 4 |
2 39 32 |
28 143 36 |
25 |
|
12 9 0 |
10 81 15 |
2 36 35 |
24 126 50 |
26 |
|
14 14 0 |
12 168 8 |
0 28 40 |
26 210 48 |
27 |
|
15 30 2 |
9 105 10 |
3 60 16 |
27 195 28 |
28 |
|
36 62 0 |
20 104 20 |
0 26 30 |
56 192 50 |
29
|
|
20 14 0 |
16 154 24 |
4 42 42 |
40 210 66 |
30 |
|
49 48 3 |
14 160 12 |
0 16 15 |
63 224 30 |
1) Найти матрицу Р вероятностей перехода.
2)
Найти вектор состояния системы через
два года
![]() .
.
2. Найти матрицу вероятностей перехода, если соответствующий размеченный граф состояний имеет вид:
1.
0,75
0,1
0,2
0,9
0,05
0,35
0,55 0,1
![]()





![]()
![]()


2.
0,2
0,8
0,65
0,15 0,3
0,2
0,1
0,1 0,5

3.
0,7
0,25
0,2
0,1
0,5
0,35
0,4 0,5

4.
0,15
0,5
0,75
0,1 0,65
0,15
0,4
0,1 0,2

5.
0,3
0,4
0,5
0,2 0,25
0,6
0,3
0,3 0,15

6.
0,4
0,4
0,2 0,3
0,1
0,95
0,05 0,6

7.
0,55
0,05
0,45 0,5
0,1
0,35
0,6 0,4

8.
0,1
0,1
0,6
0,3 0,15
0,05
0,7
0,2 0,8

9.
0,7
0,6
0,3
0,4
0,15
0,2
0,2 0,45

10.
0,65
0,5
0,1
0,25 0,5
0,4
0,2
0,3 0,1

11.
0,2
0,6
0,7
0,1 0,25
0,05
0,4
0,7

12.
0,8
0,85
0,2 0,3
0,5
0,05
0,1 0,2
13.
0,5
0,1
0,4
0,7
0,15
0,15
0,85 0,15

14.
0,3
0,65
0,35 0,2
0,6
0,6
0,1 0,2
15.
0,6
0,5
0,1
0,3 0,75
0,25
0,5

16.
0,3
0,1
0,5
0,2 0,2
0,7
0,8
0,1 0,1
17.
0,1
0,1
0,45
0,45
0,3
0,4
0,5 0,7

18.
0,8
0,7
0,2
0,4
0,1
0,25
0,05 0,5
19.
0,65
0,3
0,05 0,5
0,2
0,1
0,9 0,3

20.
0,35
0,4
0,2
0,65
0,1
0,55
0,05 0,7

21.
0,5
0,6
0,05
0,45 0,2
0,15
0,3
0,1 0,65

22.
0,9
0,6
0,1 0,1
0,3
0,25
0,15 0,6
23.
0,25
0,2
0,5
0,15
0,25
0,7
0,1 0,85
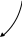
24.
0,75
0,5
0,25 0,1
0,2
0,8
0,4
25.
0,55
0,2
0,1
0,35 0,25
0,05
0,45
0,35 0,7

26.
0,35
0,2
0,8 0,4
0,5
0,65
0,1
27.
0,9
0,2
0,1 0,3
0,15
0,75
0,05 0,55

28.
0,55
0,5
0,2
0,25 0,45
0,3
0,15
0,35 0,25
29.
0,45
0,05
0,25
0,3 0,6
0,4
0,9
0,05

30.
0,6
0,25
0,4
0,35
0,3
0,55
0,2 0,35
3. Дана матрица Р вероятностей перехода Марковской системы. Построить граф состояний системы. Варианты заданий:
1)
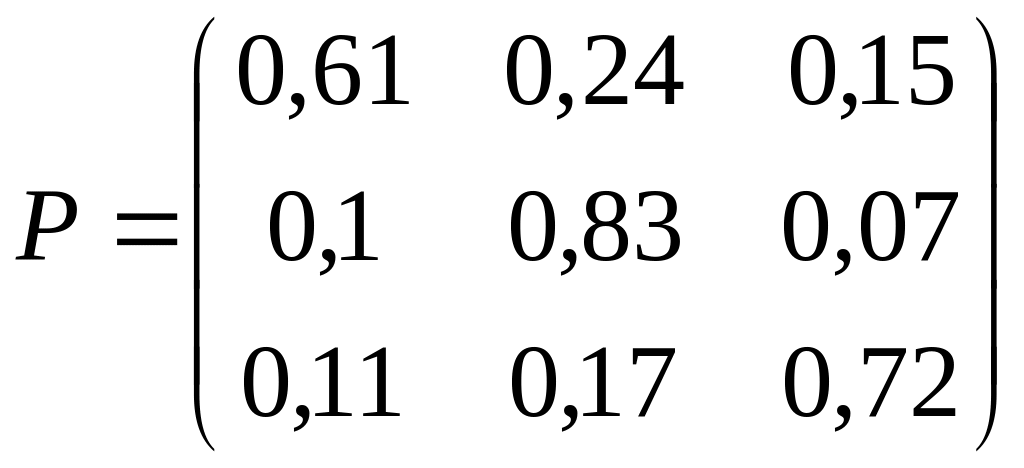 ; 2)
; 2)
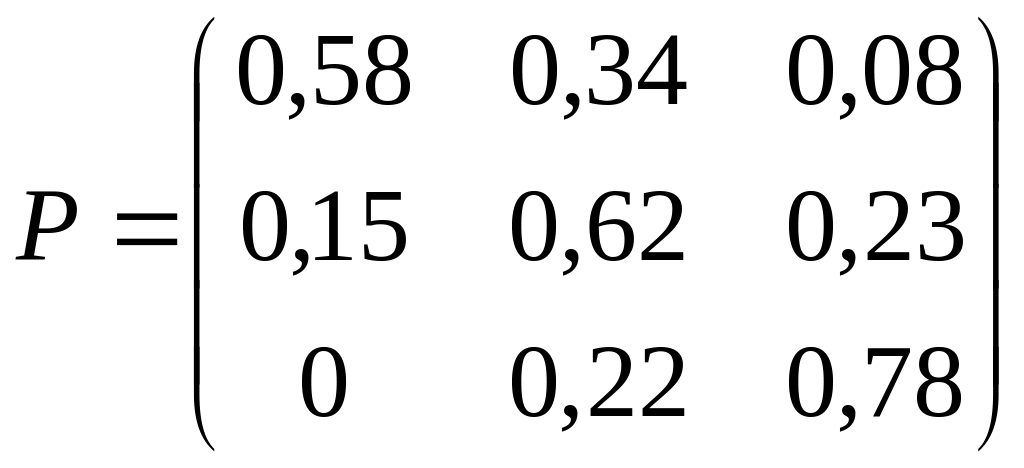 ;
;
3)
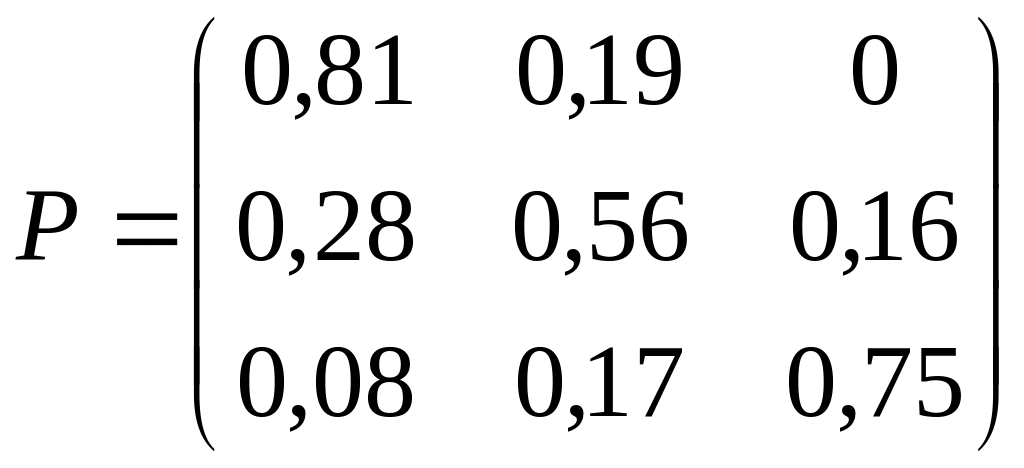 ; 4)
; 4)
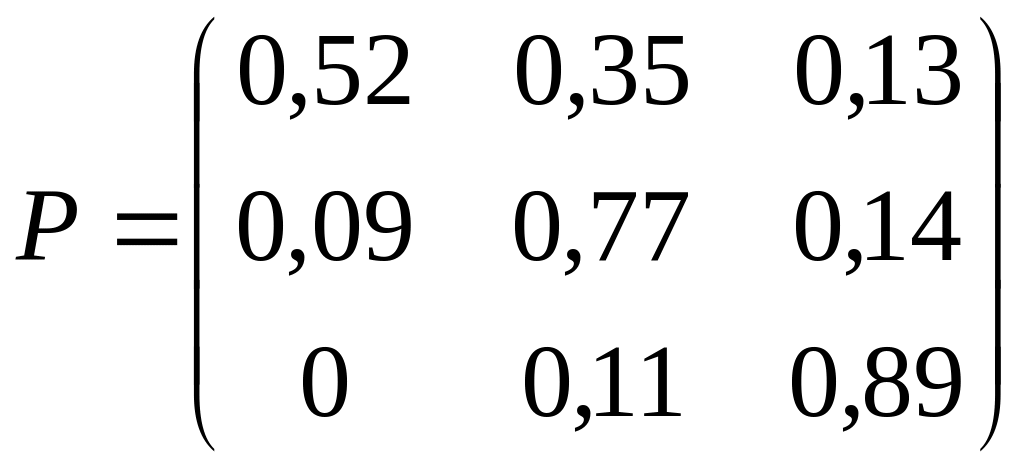 ;
;
5)
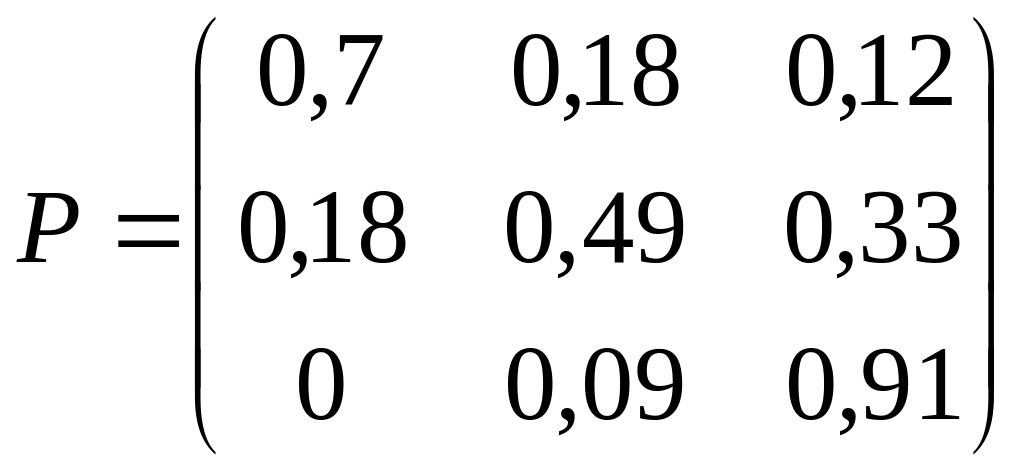 ; 6)
; 6)
 ;
;
7)
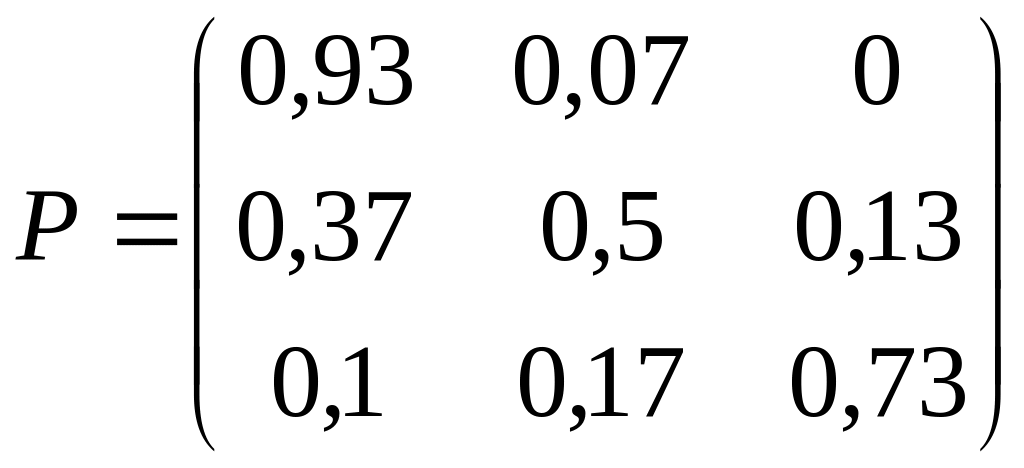 ;
8)
;
8)
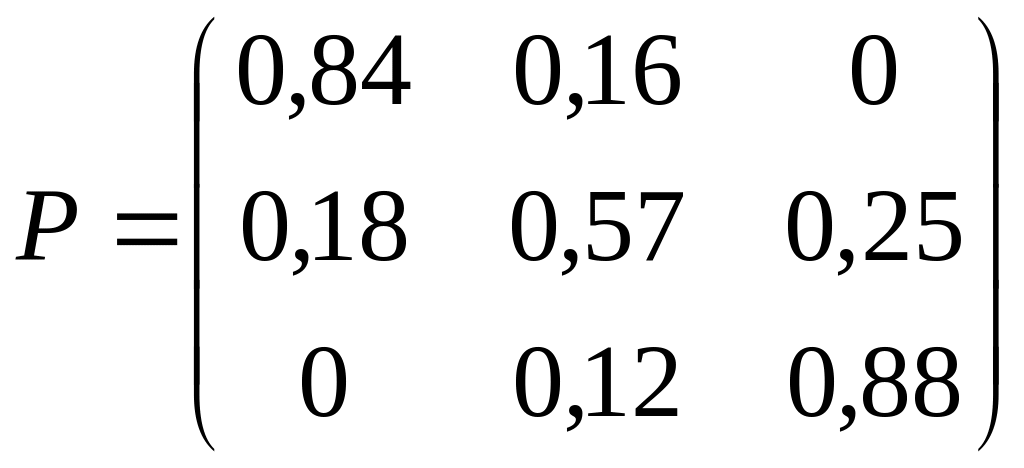 ;
;
9)
 ; 10)
; 10)
 ;
;
11)
 ; 12)
; 12)
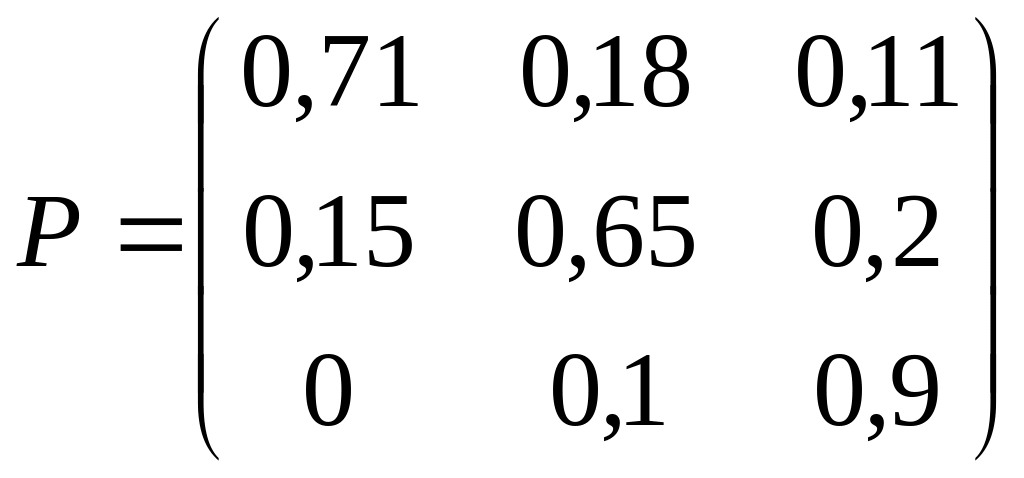 ;
;
13)
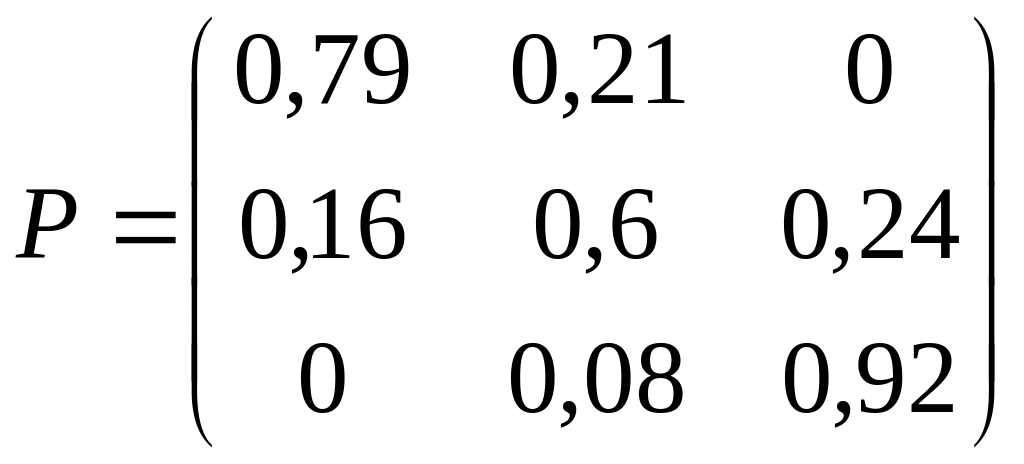 ; 14)
; 14)
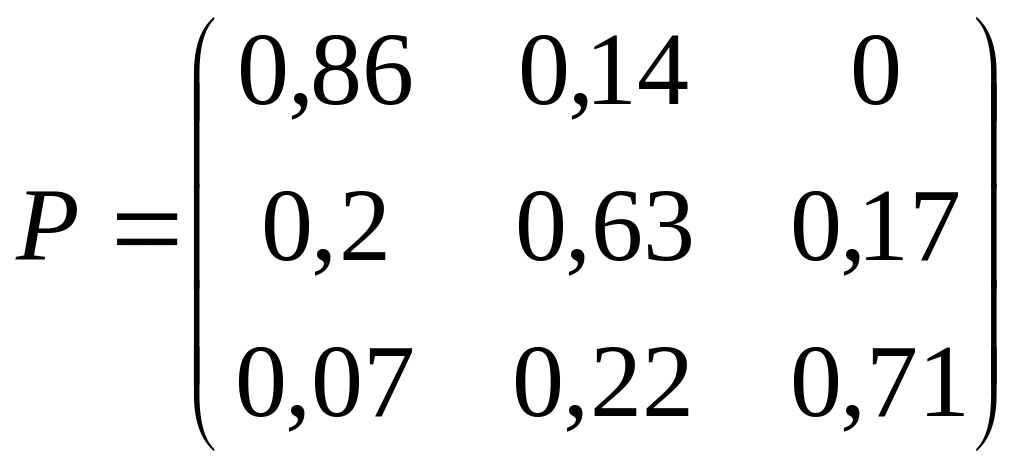 ;
;
15)
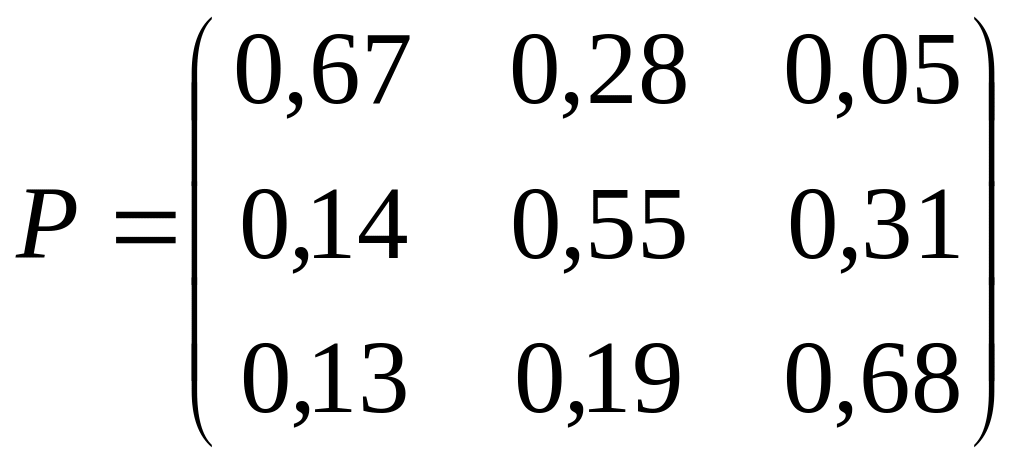 ; 16)
; 16)
 ;
;
17)
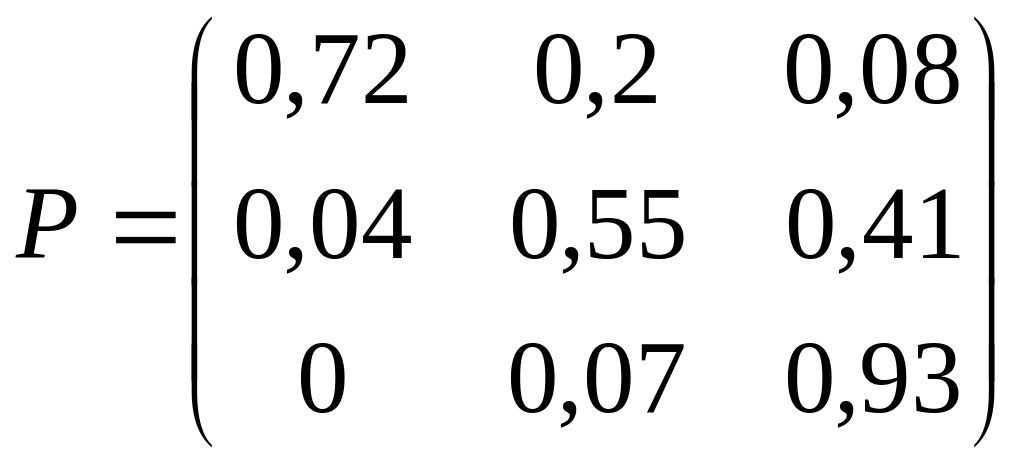 ; 18)
; 18)
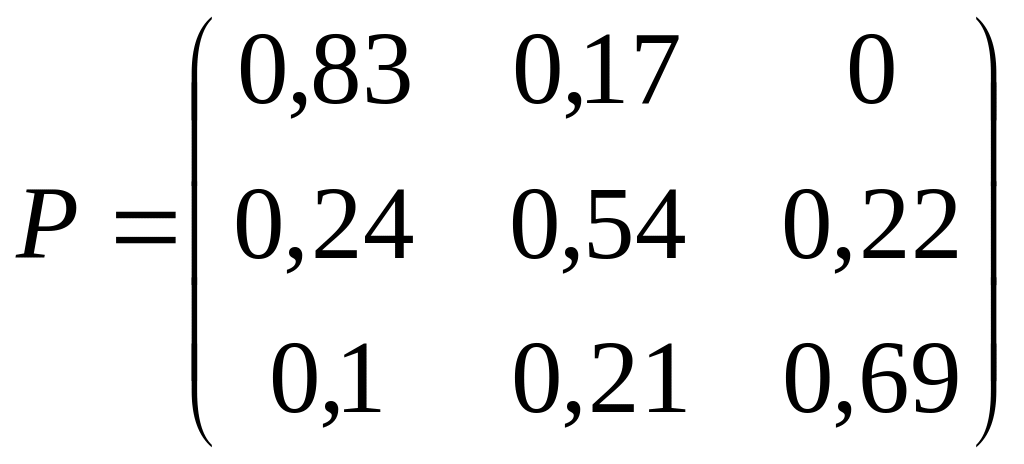 ;
;
19)
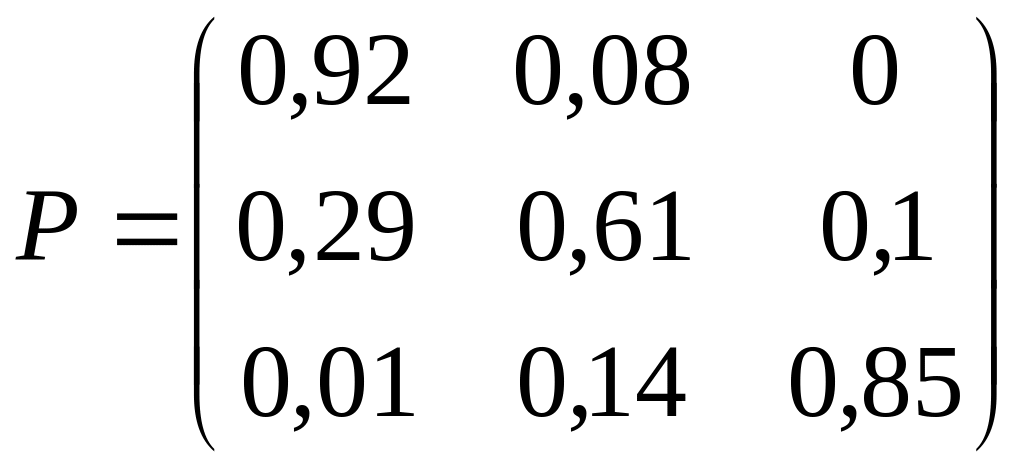 ; 20)
; 20)
 ;
;
21)
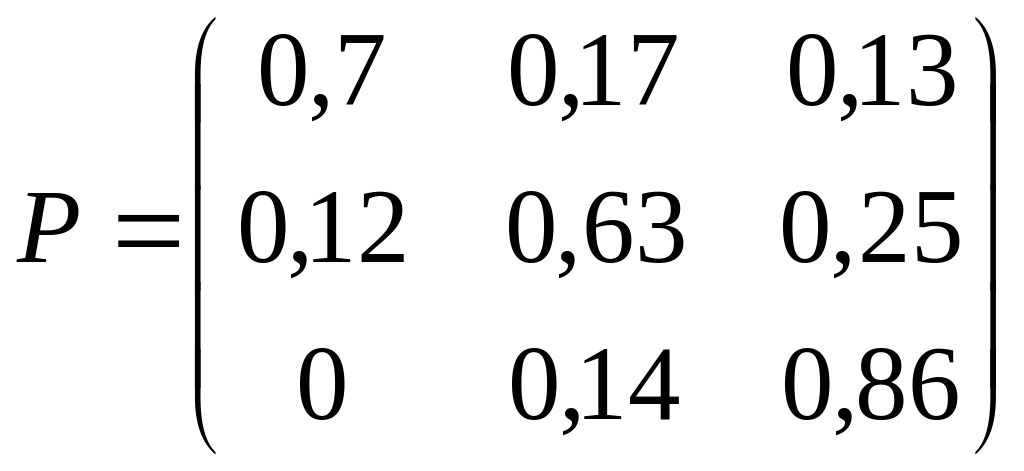 ; 22)
; 22)
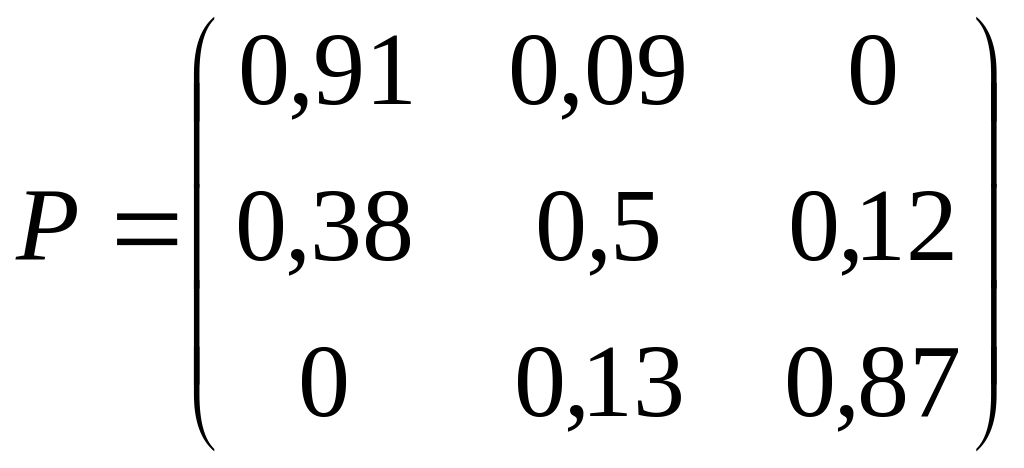 ;
;
23)
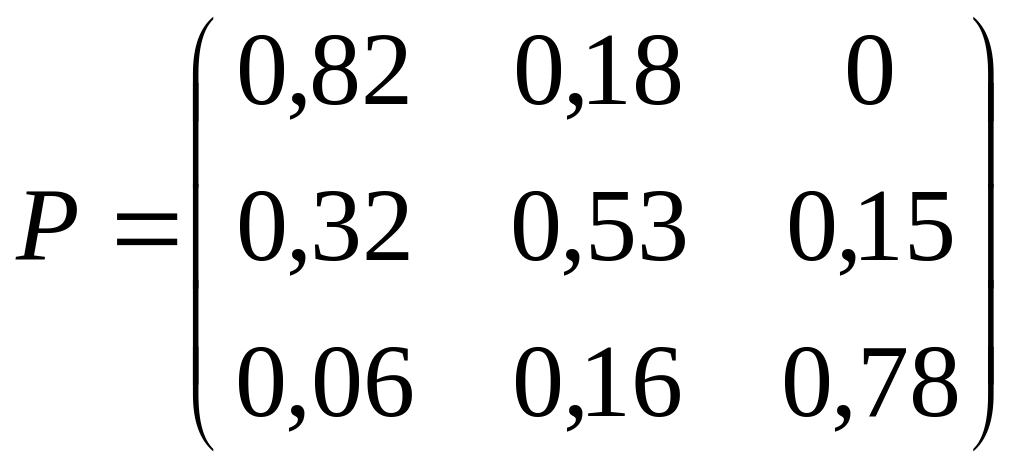 ; 24)
; 24)
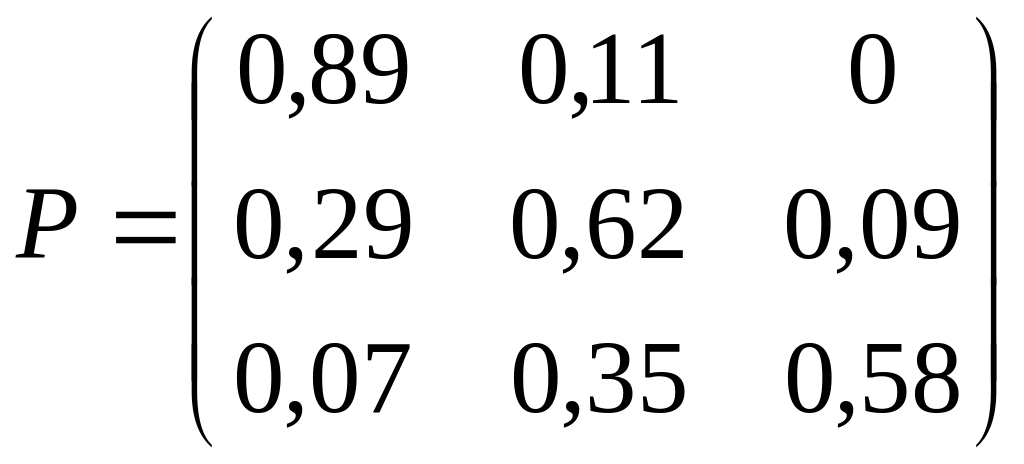 ;
;
25)
 ; 26)
; 26)
 ;
;
27)
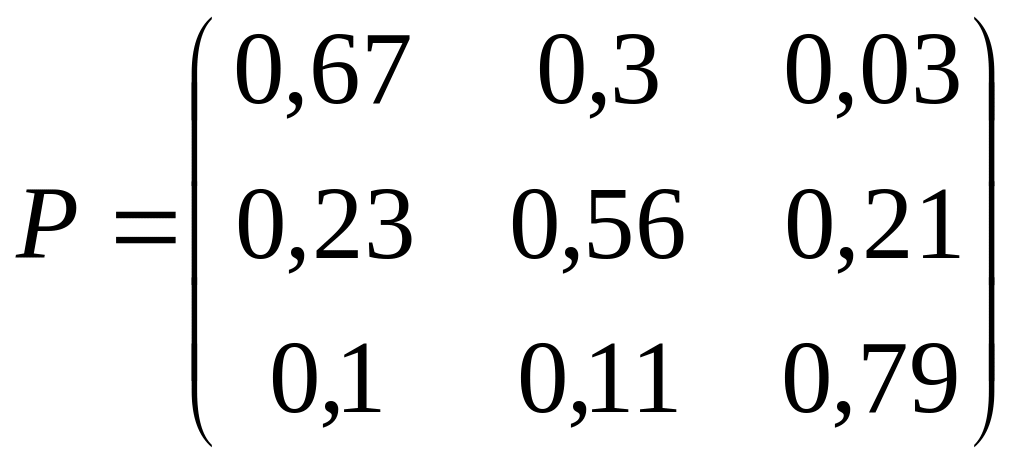 ; 28)
; 28)
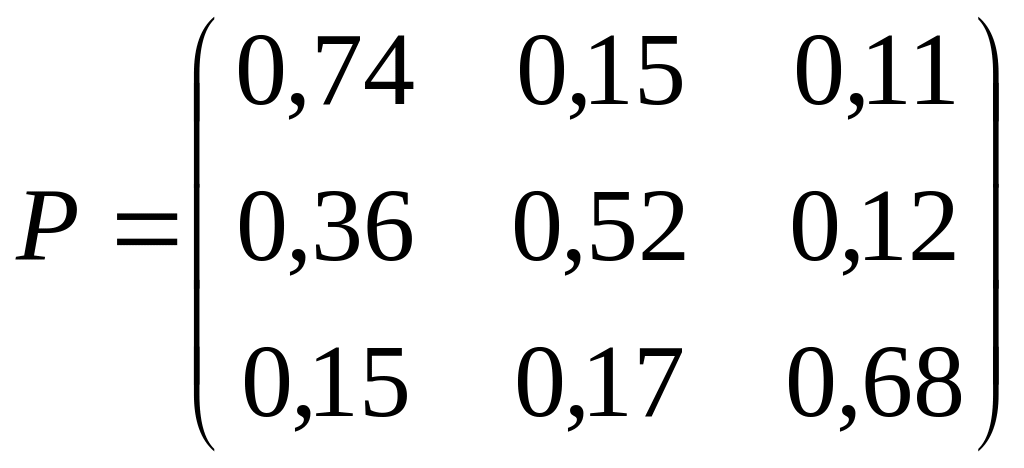 ;
;
29)
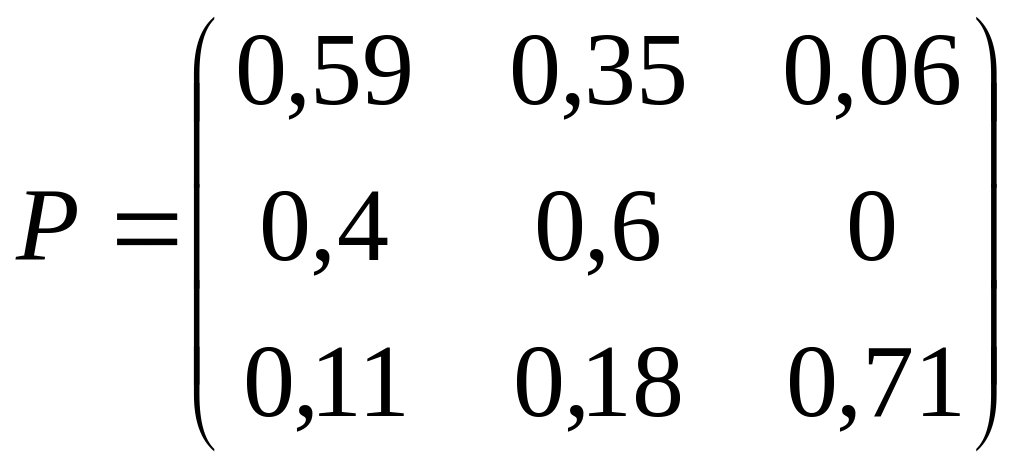 ; 30)
; 30)
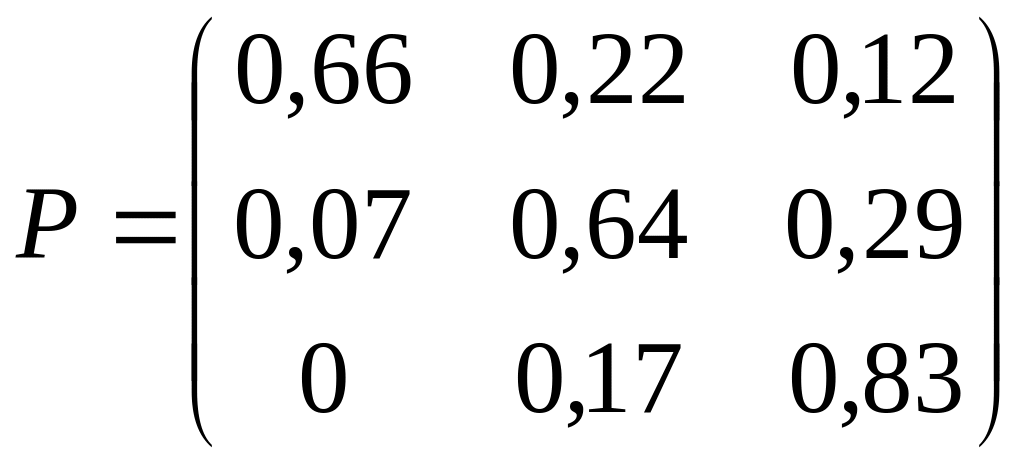 .
.
4.
Соотношение платежеспособных (состояние
)
и неплатежеспособных (состояние
)
клиентов банка в начале месяца определяется
отношением
![]() ,
а вероятности переходов между этими
состояниями по истечении месяца
характеризуются матрицей
,
а вероятности переходов между этими
состояниями по истечении месяца
характеризуются матрицей
![]() .
.
Определить отношение K в конце месяца (или в начале следующего месяца). Варианты заданий:
№ варианта |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1 2 3 4 5 6 7 |
12 9 10 8 7 11 15 |
5 3 4 3 2 3 4 |
0,8 0,7 0,6 0,5 0,4 0,9 0,7 |
0,2 0,3 0,4 0,5 0,6 0,1 0,3 |
0,4 0,2 0,1 0,3 0,2 0,3 0,4 |
0,6 0,8 0,9 0,7 0,8 0,7 0,6 |
8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
13 6 9 17 18 14 19 20 8 16 25 12 13 17 7 5 9 10 7 5 15 11 16 |
5 1 2 3 7 3 6 7 5 3 4 7 3 4 3 1 4 3 1 2 2 4 5 |
0,6 0,8 0,5 0,4 0,9 0,3 0,7 0,8 0,6 0,5 0,4 0,9 0,8 0,3 0,6 0,8 0,7 0,5 0,8 0,7 0,6 0,9 0,8 |
0,4 0,2 0,5 0,6 0,1 0,7 0,3 0,2 0,4 0,5 0,6 0,1 0,2 0,7 0,4 0,2 0,3 0,5 0,2 0,3 0,4 0,1 0,2 |
0,5 0,1 0,4 0,7 0,2 0,8 0,1 0,3 0,2 0,3 0,1 0,4 0,2 0,6 0,3 0,5 0,3 0,2 0,1 0,2 0,3 0,4 0,3 |
0,5 0,9 0,6 0,3 0,8 0,2 0,9 0,7 0,8 0,7 0,9 0,6 0,8 0,4 0,7 0,5 0,7 0,8 0,9 0,8 0,7 0,6 0,7 |
Рекомендуемая литература
1. Сборник задач по математике для экономистов: учебное пособие под ред. проф. Р.Ш. Марданова. – Казань: Изд-во КГУ, 2009. - Гл.. 17, №№17.13 – 17.19.
