Властивості коефіцієнта кореляції

1. Коефіцієнт кореляції є в межах від -1 до +1.

(3.3)

Якщо , то кореляція пряма, а якщо – зворотна. Пряма кореляція: більшим значенням випадкової змінної відповідають більші значення ; зворотна кореляція: більшим значенням відповідають менші і навпаки, більшим – менші .

2. Симетрія

. (3.4)

3. Якщо та пов’язані лінійним функціональним зв’язком , і – сталі, то , і навпаки .

4. Якщо випадкові змінні лінійно незалежні, то , і навпаки.

Останні дві властивості можна сформулювати як необхідну й достатню умови, причому критерієм залежності випадкових величин і є відмінність коефіцієнта кореляції від нуля: .

Вибірковий коефіцієнт кореляції

Розрізняють істинний коефіцієнт кореляції та його оцінку за вибіркою , що є випадковим числом. Вибірковий коефіцієнт кореляції знаходять за формулою

. (3.5)

Для малого обсягу даних значення буде заниженим порівняно з істинним коефіцієнтом кореляції . Тому для рекомендують використовувати уточнену оцінку

. (3.6)

Кореляційне поле

Графічно дані для кореляційного аналізу зображають у вигляді кореляційного поля, тобто точок на площині, кожна з яких має координати (рис. 3.1).

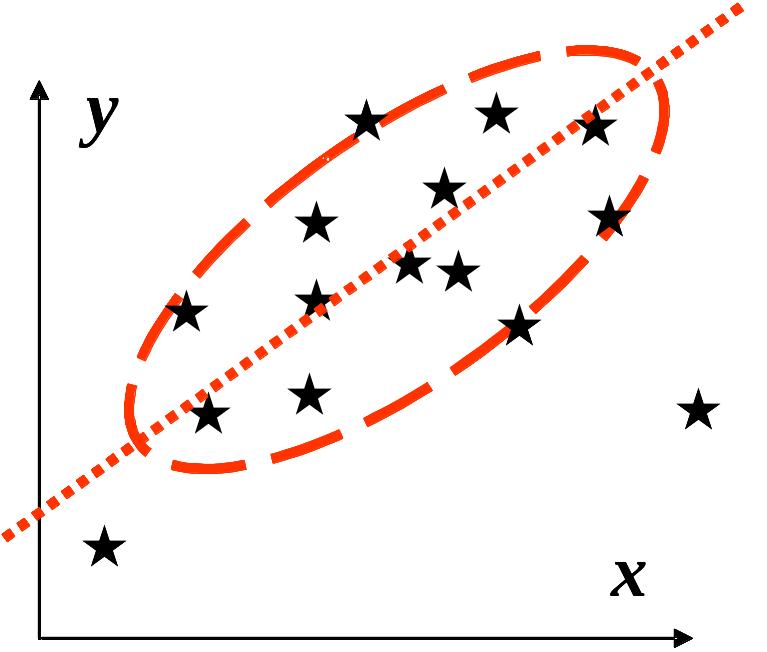
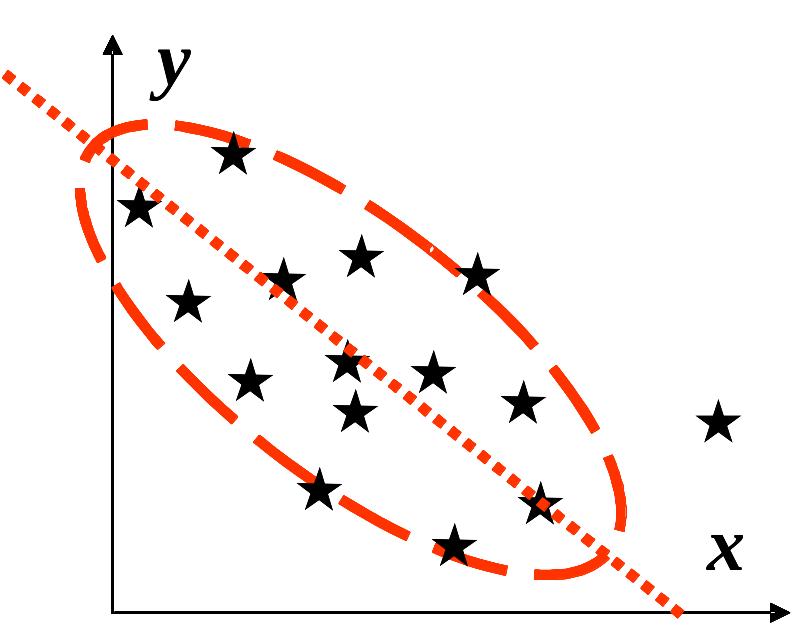
а б

Рис. 3.1. Візуальна оцінка характеру кореляційного зв’язку за кореляційним полем: а – пряма кореляція, ; б – зворотна кореляція, .

Для прямої кореляції характерною тенденцією є збільшення одного з параметрів, якщо збільшується інший, а для оберненої, навпаки: збільшення одного супроводжується, як звичайно, зменшенням іншого. Причиною фіктивної кореляції (тобто такої, що спостережена, але не властива природним об’єктам) може бути неоднорідність сукупності даних, які відображають два різні об’єкти (рис. 3.2). Іноді методика дослідження впливає на ство­рення видимості зв’язку там, де його немає. Наприклад, якщо вимірювати довжину і ширину без урахування орієнтації зразків, то всі точки кореляційного поля лежатимуть у секторі від 0 до 45º (замість сектора 0–90º), що помилково можна сприйняти як наявність деякого зв’язку (рис. 3.3).

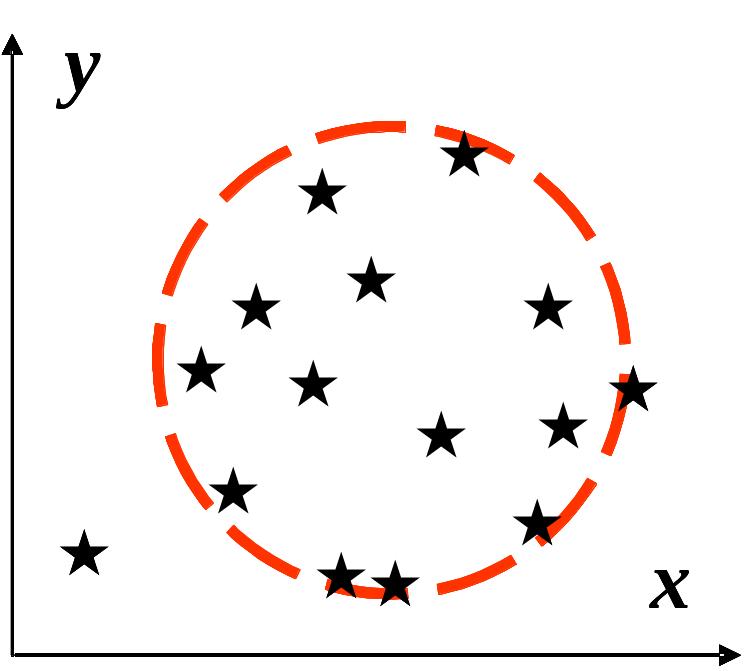
Рис. 3.2. Некорельовані дані, і фіктивна кореляція (неоднорідні дані).

Рис. 3.3. Несправжня (наведена) кореляція:

1 – істинні вимірювання; 2 – перетворені дані.

Перевірка гіпотези про значущість коефіцієнта кореляції

Згідно зі схемою статистичного доведення виконуємо таке.

1. Нульова гіпотеза: лінійного зв’язку немає, тоді істинний коефіцієнт кореляції дорівнює нулю:

: (3.7)

за двосторонньої альтернативи

: . (3.8)

2. Вибираємо , наприклад, .

3. Обчислюємо вибірковий коефіцієнт кореляції і будуємо статистику

. (3.9)

4. Ця статистика має розподіл Стьюдента з ступе­нями вільності, а для можна використовувати й стандарт­ний закон розподілу.

5. Знаходимо критичні значення статистики, тобто квантилі розподілу Стьюдента (чи стандартного для великих вибірок) для заданого рівня значущості . Для маємо

, (3.10)

а для – наближену формулу

, (3.11)

де – обернена функція стандартного закону розподілу.

6. Перевіряємо критерій: якщо , то нульову гіпотезу відхиляємо, тобто існує суттєвий лінійний зв’язок між даними (дані корелюють).

На практиці зручнішою є формула, яка дає критичне значення самого коефіцієнта кореляції. З рівняння статистики можна визначити

. (3.12)

Ця формула дає змогу один раз відшукати критичне значення коефіцієнта кореляції (для фіксованого і ) і використовувати його в наступній серії порівнянь парних коефіцієнтів кореляції з критичним, наприклад, для перевірки на значущість коефіцієнтів кореляційної матриці.

Зауваження. Для перевірки значущості коефіцієнта кореляції можна використовувати й інші статистики. Наприклад,

або (3.13)

в умовах нульової гіпотези мають -розподіл (Фішера) зі ступе­нями вільності для першої або для другої функції (3.13), відповідно.