4. Головні закони розподілу, які використовують у геостатистиці

Випадкові величини бувають дискретними і неперервними, їм відповідають дискретні й неперервні закони розподілу.

Біноміальний закон розподілу

Схема Бернуллі – це така схема послідовних незалежних проб (експериментів, спостережень), коли в кожній пробі подія A може з’явитися з імовірністю (“успіх”) і не з’явитися з імовірністю (“невдача”). Незалежність проб означає, що результат будь-якого спостереження не впливає на результати наступних спостережень, тобто ймовірність появи події A є сталою в усіх експериментах.

Якщо ймовірність задана, то ймовірність появ події A в незалежних спробах буде такою (формула Бернуллі):

, (4.1)

де – кількість комбінацій з по .

Інтегральна функція розподілу

(4.2)

Цей розподіл має два параметри: і , а математичне сподівання та дисперсія, відповідно, такі (рис. 4.1):

, .

Складність обчислень за наведеними формулами для великих зумовлює необхідність у асимптотичних наближеннях. Біноміальний розподіл є асимптотично нормальним з мате­матичним сподіванням (центром) і дисперсією (гранична теорема Муавра-Лапласа), тому нормальне наближен­ня (якщо ) описує формула:

(4.3)

(4.4)

а ймовірність появи від до вдалих результатів

. (4.5)

Закон розподілу Пуассона

Інше наближення, пуассонівське, використовують для густи­ни (4.1), якщо :

, (4.6)

де – параметр розподілу, який дорівнює математичному сподіванню та дисперсії,

. (4.7)

Закон розподілу Пуассона можна отримати з біно­міального розподілу граничним переходом при і , так що добуток є скінченним числом. Цей закон застосовують, коли треба визначити кількість появи деякої події для великої кількості спроб та малої ймовірності появи події в окремій спробі, . Густину розподілу описує формула (4.6), а функція розподілу:

. (4.8)

Рис. 4.1. Біноміальний закон розподілу 1, 2, 3 та нормальне наближення 4.

Нормальний закон розподілу, або розподіл Гауcса

є неперервним розподілом випадкової величини , що характе­ризується густиною

(4.9)

та функцією розподілу

. (4.10)

Цей розподіл має два параметри: математичне сподівання та дисперсію (рис. 4.2). Після (лінійного за ) перетворення Фішера (центрування та нормалізація)

(4.11)

нова випадкова змінна матиме теж нормальний закон розпо­ділу, але вже з параметрами та дисперсією . Такий закон розподілу називають стандартним. Його функція розподілу

. (4.12)

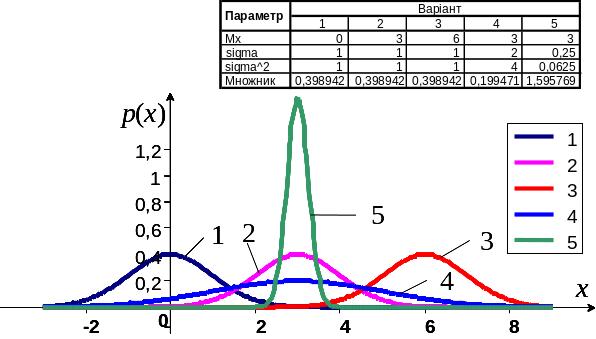
Рис. 4.2. Нормальний закон розподілу для різних параметрів і .

Квантилі нормального розподілу (з огляду на си­метрію), які визначають з умови

, (4.13)

використовують як довірчі межі нормального розподілу для заданого . Наведемо найчастіше застосовувані значення:

, , , (4.14)

а також квантилі, що кратні першим трьом стандартним відхи­ленням:

, , . (4.15)

Сформулюємо важливе для практики правило “трьох сигм”:

якщо дані підпорядковані нормальному закону розподілу, то майже вірогідно (з похибкою до 0,3%) вони повинні бути в межах від середнього значення (математичного сподівання).

Важливість нормального закону розподілу в природничих науках зумовлена тим, що він задовільно апроксимує розподіл значень багатьох кількісних показників, спричинених дією бага­тьох рівносильних факторів. Тому його можна приймати (хоч і не завжди) як імовірнісну модель досліджуваного явища. Однак з погляду інтерпретації така модель не повинна суперечити тим теоретичним передумовам (геофізичним, хімічним та ін.), що характеризують природу цього явища. У геології нормальний закон розподілу – один із головних, хоча є багато явищ, імовір­нісна модель яких значно відхиляється від нормального закону, що може бути зумовлене порушенням умов рівномірної малості і незалежності впливу факторів, що генерують досліджувану випадкову величину.