Три типи математичних моделей

Рис. 1.2. Рис. 1.3.

Математичні моделі можна класифікувати так.

1. ПРИЧИННО-НАСЛІДКОВА (ДЕТЕРМІНОВАНА МО­ДЕЛЬ), для якої маємо функціональну (відому) залежність (рис. 1.2) вихідних параметрів (реакцій) системи Y від вхідних факторів Х :

Y=F(X)

Y={Y₁, ..., Y_n}, X={X₁, ..., X_n},

де F={F_i} описують структуру системних зв’язків. Цей тип моделі стосується внутрішнього опису, що передбачає виявлення меха­нізмів взаємозв’язку між елементами системи і вже на їхній підставі визначення реакцій системи, якщо задані зовнішні фактори (пряма задача), або підбір таких зовнішніх факторів, які б давали задану реакцію системи (зворотна задача):

X=F^-1(Y).

2. АКТИВНИЙ ЕКСПЕРИМЕНТ: відомі значення факторів X, але невідомі точні значення реакції на них компонентів об’єкта (або елементів системи) (рис. 1.3):

Y=F(X)+  (X),

де  – точність, тобто похибки вимірювань, вплив неврахованих факторів, методологічна (системна) похибка. Якщо  << F(X), де (X) <  – задане мале число, то кажуть, що експеримент виконано із заданою точністю. Точність, як звичайно, вимірюють у відсотках, наприклад, значення 5% (інженерна похибка) задає широко прийнятий на практиці рівень   / F   0,05, де вираз у дужках називають ще відносною точністю (похибкою). Навпаки, вели­чину  =  Y – F(х)  називають абсолютною точністю.

Якщо похибка незначна, то маємо модель, близьку до детер­мі­ністичної (визначеної), як у випадку причинно-наслідко­вого зв’язку. Якщо ж  сумірне (одного порядку) з F(х), то величина Y буде ймовірнісною, тобто більш-менш точно передбачити наперед реакцію системи неможливо в рамках детермінованого підходу.

3. ЙМОВІРНІСНА (за природою, від початку) модель; дослідникові наперед невідомі точні значення ні факторів Х, ні реакцій Y:

П(X) П(Y),

де П – символ підмножини. Замість функціональної залежності тут розглядають залежність між підмножинами, які визначають на підставі спеціальної міри – ймовірності Р (англ. probability).

Допустимість імовірності трактування елементів, що утворю­ють множину Y, визначена, з одного боку, їхньою випадковістю, а з іншого – емпірично спостережуваною повторю­ваністю появи певних значень Y за неодноразової повторної реалізації ком­плексу зовнішніх умов F  П(х).

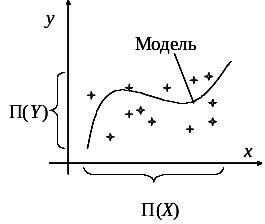Рис. 1.4.

Роль математичної статистики в опрацюванні геологічних даних

Одні з найпростіших системних моделей у геології – імовірнісні (статистичні). Їхня мета полягає в математичному опрацюванні значних обсягів інформації (даних вимірювань), відображеної в цифрах. Як звичайно, статистичні моделі викори­стовують для зовнішнього опису системи, коли природа взаємо­зв’язків між елементами системи маловивчена або несуттєва.

Математична статистика займається плануванням і ста­тистичним описом результатів досліджень, побудовою та пере­віркою математичних моделей для масових випадкових подій.

Геостатистика є прикладною дисципліною і визначає правила й можливості застосування математичної статистики в комплексі наук про Землю. У вужчому значенні геостатисти­ка – це математична теорія розвідування корисних копа­лин та оціню­вання їхніх просторових властивостей. З іншого боку, саме прикладні задачі (практика опрацювання даних вимірювань) були і є стимулом розвитку теоретичних основ математичної ста­тистики.

Умови коректного застосування методів математичної статистики такі.

Масовість означає, що хоча окремий результат вимірювання не є точним, та у разі повторних вимірювань результат (змінну величину) можна оцінити з набагато ліпшою точністю.

Сукупність спостережень називають ще статистичним матеріалом, а їхню кількість – обсягом (розміром, об’ємом, довжиною, тривалістю: залежно від природи вимірювань) спосте­режень. За обсягом статистичний матеріал класифікують на малий (до 20 спостережень), середній (20–50 спостережень), великий (50–500), дуже великий (500–1000) і надвеликий (це тисячі спостережень).

Випадковість означає, що результат окремого вимірювання є наперед невідомим. У практиці геологічних досліджень цього досягають спостереженнями на рівномірній сітці (якщо можливо) або максимальним зменшенням впливу суб’єктивного фактора. Часто доводиться згущувати (деталізувати) дослідження в певній зоні. Умова випадковості в цьому випадку теж порушується. Очевидно, що статистичний матеріал для цієї зони треба розглядати окремо.

Умова незалежності результатів спостережень від попе­редніх (і наступних у випадку наявності зворотного зв’язку) або координат простору. Геологічні об’єкти і процеси часто мають просторові та часові залежності, тобто умова незалежності не виконується, що суттєво звужує область застосу­вання статистич­них математичних моделей. Однак деколи цими закономірно­стя­ми можна знехтувати. Наприклад, коли мінли­вість, спричинена похибкою вимірювань, сумірна з природною мінливістю.

Четверта, остання умова – однорідність спостережень – поля­гає в тому, що статистичний матеріал повинен належати одному геологічному об’єкту і бути отриманий однаковими мето­дами, приладами тощо.

Приклад: асоціації хімічних елементів у мінералі чи мінералів у породі. Якщо межі геологічного об’єкта задані якісно і наперед, то в результаті кількісного аналізу взаємозв’язків між його складовими може виявитися суттєво різна внутрішня структура (походження, генезис) подібних об’єктів (процесів). Тоді стати­стичний матеріал треба вміти розділити на декілька однорідних сукупностей з урахуванням виявленої структури взаємозв’язків.

Знову ж таки, на практиці геологи працюють з даними, отри­маними в різні роки, різними дослідниками, різними приладами, на підставі різних методологій досліджень, уявлень про процес чи внутрішню структуру геологічних об’єктів. Це знижує ефектив­ність методів математичної статистики в геології.

Якщо ці чотири умови виконуються, то статистичний мате­ріал відображає статистичну змінну (змінну величину, варі­анту). Тут слово статистична означає, що пізнати цю величину (варіанту) можна в результаті реєстрації низки її проявів (ознак), тобто збирання статистичного матеріалу.

Існує декілька підходів до класифікації статистичних змін­них. Згідно зі шкалами вимірювань їх поділяють на якісні, порядкові (або рангові) та кількісні; за щільністю значень – на дискретні та неперервні, а за кількістю виміряних параметрів – на одно-, дво- і багатовимірні. Наприклад, дані щодо свердловин є дискретними стосовно просторового характеру простягання геологічного поля, водночас ці дані неперервні стосовно глибини для окремої свердловини. Отже, наведені класифікації не є взаємно незалежними.

Статистичні математичні моделі в геології є одними з найпростіших. Унаслідок обмеженої кіль­кості вимірювань (спо­стережень) вони допускають отримання помилкових результатів або висновків, які, отже, є відносними (імовірнісними). Крім того, статистичні моделі дають змогу оцінити кількісні зв’язки (пропорції) між геологічни­ми об’єктами чи його озна­ками, але не дають інформації про природу цих зв’язків. Це є завданням інтерпретації результатів, у нашому випадку, геологічної, геофізичної чи геохімічної інтерпретації.

Приклад. Нехай виявлено, що в деякому мінералі А вміст одного хімічного елемента становить 10–15%, іншого – 40–60%, ще іншого – 5–10%. Математична статистика не дає відповіді на запитання: чому саме стільки відсотків, а не більше чи менше. Мабуть, повинно бути генетичне пояснення походження цього мінералу внаслідок фізико-хімічних умов, геологічних процесів тощо. З іншого боку, ці кількісні показники можуть слугувати класифікації невідомих зразків щодо зачислення їх до мінералу А.

В основі статистичного моделювання є поняття генеральної сукупності та вибірки. Генеральна сукупність – це абстрактне математичне поняття, яке охоплює всі можливі прояви (значення) випадкової величини (статистичної змінної), що характеризує об’єкт. Вибірка – це сукупність спостережень (вимірювань) цієї випадкової величини.

Приклад. Нехай у непрозорому ящику лежить три кулі: си­нього (С), зеленого (З) і червоного (Ч) кольору. Беремо навмання кулю. Реєструємо її колір і кладемо назад у ящик. Повторюємо декілька разів. Нехай наш запис містить: ССЗСЧЗ – це вибірка з шести спостережень. СЗЧ – генеральна сукупність. Зазначимо, що за цією вибіркою генеральна сукупність оцінена повністю, тобто ми виявили всі три можливі кольори кульок. Якщо б у наведеній вибірці взяти не більше чотирьох спостережень, то червоний колір кульок не був би виявлений, і висновок про те, що в ящику кульки лише двох кольорів, був би хибним.