Похибки першого й другого роду

Результати статистичного доведення можна навести у вигляді таблиці:

H0	Правильна	Хибна
Приймають	+	Помилка другого роду,
Відкидають	Помилка першого роду,	+

Як звичайно, нульову гіпотезу формулюють так, щоб нега­тив­ний вплив (шкода) помилки першого роду був меншим, ніж вплив помилки другого роду. З імовірністю ми можемо помил­ково віднести дані, що відповідають гіпотезі H₀, до H₁. Мірою якості критерію, або потужністю критерію, є число 1- (рис.6.1).

Рис. 6.1. Розподіли і значень функції-статистики, якщо правильна нульова гіпотеза чи проста альтернативна гіпотеза, відповідно. Тут: – критичне значення статистики, що відділяє область прийняття нульової гіпотези (з рівнем значущості ) від критичної області (нульову гіпо­тезу відкидаємо); – ймовірність помилки другого роду.

Параметричні й непараметричні критерії

Статистичні критерії поділяють на параметричні і непараме­тричні. Для застосування параметричних критеріїв необхідно перевірити виконання додаткових умов, наприклад, підпорядку­вання вибірки певному закону розподілу. Непараметричні ж критерії не потребують додаткових перевірок, але мають меншу потужність.

Критерій погодженості хі-квадрат

Цей критерій використовують для перевірки частотного розподілу деяко­го параметра двох об’єктів або вибірки і заданого розподілу (планового теоретичного, еталонного об’єкта).

Нехай задано вибірку, яку можна розбити на k класів (груп). Класи вибирають так, щоб у кожному з них було достатньо значень (не менше шести-восьми), інакше класи об’єднують. Завдання полягає в перевірці гіпотези, що кількість появи значень у кожному з класів (інтервалів) узгоджується із заданим. Схема статистичного доведення така.

1. Формулювання гіпотези

H₀: для всіх ;

H₁: хоча б для одного ,

де – фактична кількість – частота – (експериментальних) даних в i-му класі; – очікувана (планова, теоретична) кількість даних в i-му класі; – кількість класів (груп); – частотне відношення; – теоретична ймовірність.

2. Вибір рівня значущості .

3. Обчислюємо статистику Пірсона

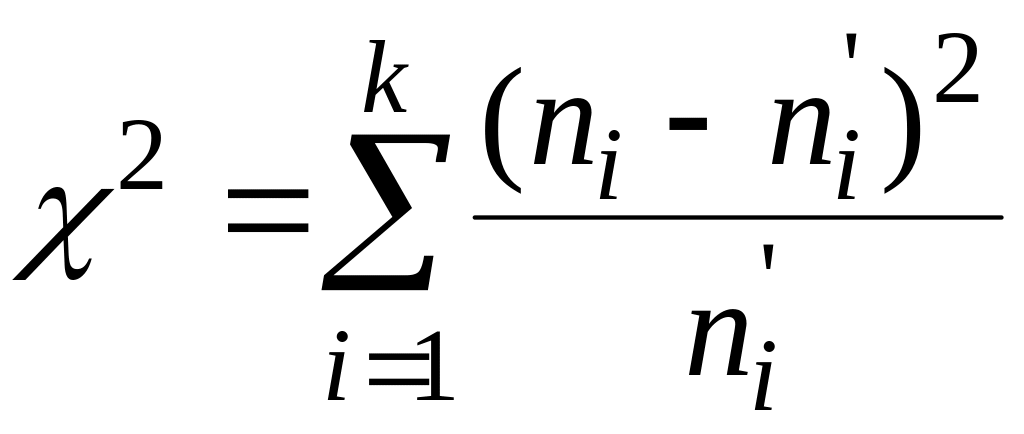або . (6.1)

4. Статистика має однойменний розподіл (Пірсона), з ступенями вільності ( – “degree of freedom” (англ.) – ступені вільності). Якщо теоретичний закон розподілу має параметри, які оцінюють на підставі вибірки (наприклад, середнє та дисперсія для нормального закону розподілу), то додатково потрібно зменшити на кількість оцінюваних параметрів (тому для нормального розподілу матимемо ).

5. Знаходимо критичні значення статистики .

6. Перевіряємо критерій: якщо , то порівню­вані розподіли статистично не відрізняються.

Приклад. Перевірити узгодженість експериментальних даних нормальному закону розподілу.

Статистичний матеріал розбиваємо на класи (з вико­ристанням формули Стеджерса або з інших міркувань, наприклад, з урахуванням правила “трьох сигм”). Для ефективності критерію домагаємося, щоб кількість класів була не менше шести–семи, а кількість даних у кожному класі – не менше п’яти. Інакше потрібно збільшити сусідні класи. Отже, можна вважати, що критерій ефек­тивно застосовувати, якщо обсяг вибірки досягає 50–60 значень.

Далі знаходимо точкові оцінки математичного сподівання та дисперсії (або стандартного відхилення): . Ступені вільності: . Для обчислення теоретичної кількості значень в i-му класі скористаємося властивостями частотного відношення та інтегральної функції розподілу :

, (6.2)

де – межі (інтервал) k-го класу. Обчисливши статистику (6.1) і знайшовши для неї верхнє критичне значення , робимо висновок щодо нульової гіпотези . Очевидно, що для добре узгоджених теоретичного й експери­ментального розподілу значення повинне бути малим, тому розглядаємо тільки праву альтернативу .