
- •Глава 13. Экономико-математические модели
- •13.1. Математические модели и точность
- •13.2. Равновесие спроса и предложения
- •13.3. Максимальная прибыль
- •13.4. Предельный анализ в экономике
- •13.5. Эластичность экономических функций
- •13.6. Зависимость спроса от цен и доходов
- •13.7. Экономический смысл частных производных
- •13.8. Полезность товаров и услуг
- •13.9. Балансовые модели
- •13.10. Цепи Маркова
Глава 13. Экономико-математические модели
13.1. Математические модели и точность
экономических расчётов
Всякая теория является своеобразной приставкой к измерительным средствам, существенно расширяющей объём информации, который они дают. Как и измерительные средства, математическая модель имеет погрешность, мерой которой является расхождение её предсказаний с практикой.
Широко применяющийся в настоящее время термин «математическая модель» вошёл в употребление сравнительно недавно – лет 50 тому назад. Ранее это же самое называли и проще и точнее – «приближённая теория» (такого-то явления), причём само собой подразумевалось, что каждое явление может быть описано несколькими вариантами теории, обладающими разными уровнями погрешности. Недостаток термина «математическая модель» состоит в том, что в нём отсутствует существенный эпитет «приближённая», подчёркивающий существование связи «модели» с описываемым ею явлением и неполную адекватность этой связи. Это иногда даёт повод для формально-математического подхода к моделям в отрыве от тех конкретных задач, для решения которых они предназначены.
При рассмотрении любой задачи (экономической, социологической, экологической, управленческой и т. п.) на основании её математической модели не следует забывать как о конечной цели расчёта, которой является отнюдь не число, а получение информации о картине рассматриваемого явления и о взаимном влиянии характеризующих его параметров, так и о погрешности математической модели.
Что касается точности экономических расчётов, то следует помнить, что «первое правило всяких вычислений состоит в том, чтобы точность результатов, ими доставляемых, соответствовала той практической потребности, для которой вычисления производятся. Очевидно, что расчёты не точны, но слова «не точны» не равносильны словам не пригодны для дела» (из доклада академика А.Н. Крылова председателю Морского технического комитета, 1904 г.).
13.2. Равновесие спроса и предложения
Микроэкономика занимается анализом деятельности отдельных звеньев хозяйственной системы. Это могут быть отдельные фирмы, предприятия, рынки конкретных видов товаров и услуг и т. д. Один из важнейших вопросов микроэкономики состоит в изучении взаимодействия спроса и предложения.
Спрос на данный товар – это потребность в определённом количестве товара, ограниченная действующими ценами и платёжеспособностью потребителей. Предложение можно определить как количество товара, которое может быть представлено на рынке для продажи по данной цене.
Выпуск дополнительной продукции требует дополнительных затрат. Чтобы побудить к этому производителя, надо предложить ему повышенную цену, т. е. предложение является некоторой функцией цены. Если обозначить предложение через S, а цену через P, то сказанное выше можно записать в виде
![]() .
(13.1)
.
(13.1)
Эта функция может быть достаточно сложной, и, кроме того, предложение S может зависеть не только от цены на товар P, но и от других факторов. Этими факторами сейчас пренебрежём. В экономике график зависимости предложения от цены называется кривой предложения. Экономисты предпочитают независимую переменную P откладывать на вертикальной оси координат, а значение функции S – на горизонтальной оси. Разрешая равенство (13.1) относительно цены P, можно записать его в виде:
![]() ,
(13.2)
,
(13.2)
где
![]() функция,
называемая обратной функцией по
отношению к
функция,
называемая обратной функцией по
отношению к
![]() и
имеющая графиком ту же кривую предложения.
и
имеющая графиком ту же кривую предложения.
Конкретный вид зависимости (13.2) может быть получен или из статистических данных, или из экономической теории. Сделаем предположение, что эту зависимость можно представить в первом приближении самой простой, а именно линейной функцией:
![]() ,
(13.3)
,
(13.3)
где
![]() и
и
![]() некоторые
постоянные величины, называемые
параметрами и определяемые
эмпирически.
некоторые
постоянные величины, называемые
параметрами и определяемые
эмпирически.
Разумеется, предположение о линейной зависимости цены P от предложения S является сильным упрощением действительности. Однако, во-первых, линейная функция самая простая и анализировать её легче всего, во-вторых, это даёт возможность хотя бы немного приблизиться к решению задачи. Такой приём, при котором мы выделяем некоторые существенные черты из реальной задачи, а потом делаем упрощающие предположения, получил название «моделирование». При этом реальная задача «заменяется» какой-либо моделью, исследуя которую мы можем делать предсказания. Чем ближе модель к действительности, тем она сложнее и тем точнее предсказания, которые можно с её помощью сделать.
Экономическая теория и здравый смысл
подсказывают, что предложение товара
растёт с ростом цены. Действительно,
чем выше цена на товар, тем большее число
производителей стремится предложить
этот товар на рынке. Это, в свою очередь,
означает, что функция (13.3) является
возрастающей функцией, т. е.
![]() (рис. 96).
(рис. 96).
Займёмся теперь изучением кривой спроса. В отличие от кривой предложения она является убывающей функцией. Действительно, если цена на какой-то товар растёт, то количество проданного товара будет уменьшаться. Предположим теперь, что и кривую спроса можно в первом приближении также представить прямой линией. Тогда, будучи убывающей функцией, кривая спроса может быть записана в виде:
![]() ,
,
![]() ,
(13.4)
,
(13.4)
г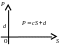
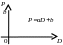 де
де
![]() цена,
цена,
![]() спрос,
спрос,
![]() и
и
![]() постоянные
величины, т. е. параметры. График кривой
спроса в линейном приближении изображён
на рис. 97.
постоянные
величины, т. е. параметры. График кривой
спроса в линейном приближении изображён
на рис. 97.
Рис. 96 Рис. 97
Спрос и предложение относятся к какому-то
определённому виду товара или группе
товаров. Количество товара в зависимости
от вида может измеряться в различных
единицах: автомобили в штуках, нефтепродукты
в тоннах и т. д. Важно, что эти единицы
для спроса и предложения одни и те же.
Поэтому, обозначая количество товара
буквой
![]() ,
мы можем кривые спроса и предложения
изобразить на одном графике (рис. 98).
,
мы можем кривые спроса и предложения
изобразить на одном графике (рис. 98).
В микроэкономике представляет интерес
точка пересечения кривых спроса и
предложения. Эта точка называется точкой
равновесия, соответствующая
ей цена![]() равновесной
ценой, а количество товара
равновесной
ценой, а количество товара
![]() с равновесной ценой
равновесным
объёмом спроса
– предложения. Такие названия
связаны с тем обстоятельством, что в
точке равновесия спрос приходит в
соответствие с предложением, т. е. весь
произведённый товар находит своего
покупателя, и все желающие купить данный
товар имеют возможность сделать это.
с равновесной ценой
равновесным
объёмом спроса
– предложения. Такие названия
связаны с тем обстоятельством, что в
точке равновесия спрос приходит в
соответствие с предложением, т. е. весь
произведённый товар находит своего
покупателя, и все желающие купить данный
товар имеют возможность сделать это.
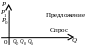
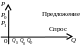
Рис. 98 Рис. 99
Не меньше чем равновесная цена представляет
интерес и отклонение рыночной цены
от равновесной. Из рис. 98 видно, что если
рыночная цена
![]() больше равновесной цены
больше равновесной цены
![]() ,
то количество товара
,
то количество товара
![]() ,
отвечающее предложению, больше количества
товара
,
отвечающее предложению, больше количества
товара
![]() ,
отвечающего спросу, т. е. предложение
превышает спрос. Следствием этого
будет оседание нереализованной продукции
на складах. В свою очередь это будет
побуждать производителей уменьшить
цену на продукцию, т. е. рыночная цена
будет стремиться к равновесной цене
.
Это явление известно как «давление
рынка».
,
отвечающего спросу, т. е. предложение
превышает спрос. Следствием этого
будет оседание нереализованной продукции
на складах. В свою очередь это будет
побуждать производителей уменьшить
цену на продукцию, т. е. рыночная цена
будет стремиться к равновесной цене
.
Это явление известно как «давление
рынка».
Предположим теперь, что рыночная цена меньше равновесной цены . Из рис. 99 видно, что в этом случае количество товара , соответствующее рыночной цене , меньше количества товара , определяемого спросом по той же рыночной цене . Это в свою очередь означает, что спрос превышает предложение. В такой ситуации производители товара, пользуясь дефицитом, повышают цену, т. е. рыночная цена вновь стремится к равновесной цене . Таким образом, установление равновесной рыночной цены данного товара в условиях конкурентного рынка формируется паутинообразной моделью.
Необходимо подчеркнуть, что рассмотренная экономико-математическая модель сильно упрощает действительность. Во-первых, она содержит предположение о линейности функций спроса и предложения. Во-вторых, спрос и предложение зависят не только от цены, но и от ряда других факторов. Некоторые из этих факторов будут рассмотрены позже с помощью функций нескольких переменных.
