Тема 15 Соотнесение графика квадратичной функции с формулой
Функция
вида
,
где
,
b,
c
— числа; x
— независимая переменная, называется
квадратичной функцией.
1
.
а)
О.О.Ф.
б) О.З.Ф.
в)
нули функции:
г) Монотонность функции
,
если
,
если
д) ось симметрии — ось ординат
2
.
Коэффициент а отвечает за сужение параболы вдоль оси ординат;
если
,
то ветви расположены дальше от OY;
если
,
то ветви расположены ближе к OY.
3.
К
оэффициент
с
отвечает за перемещение параболы вдоль
оси ординат;
если
,
то график
поднимается вверх на с;
если
,
то график
поднимается вверх на с.
4
.
Коэффициент
b
отвечает за перемещение вдоль оси OX;
если
,
то влево на b
единиц от 0; если
то вправо на b
единиц от 0.
5
.
Пример:
Тема 16 Чтение графика реальной зависимости
Теория |
Практика |
Правило (закон) соответствия между множествами X и Y, по которому для каждого элемента из множества X можно найти один и только один элемент из множества Y, называется функцией. Множество X всех допустимых действительных значений аргумента x, при которых функция y = f (x) определена, называется областью определения функции. Множество Y всех действительных значений y, которые принимает функция, называется областью значений функции. Функция считается заданной, если: - задана область определения функции X ; - задана область значений функции Y ; - известно правило ( закон ) соответствия, причём такое, что для каждого значения аргумента может быть найдено только одно значение функции. Это требование однозначности функции является обязательным. Графиком функции называется множество точек, удовлетворяющих у=f(х).
Представляет
значительный практический
интерес
другая задача: задан
график
Подобные задачи часто решаются в ходе экспериментальных исследований. Построение графиков при этом осуществляется разными методами. Например, по точкам, найденным экспериментально. |
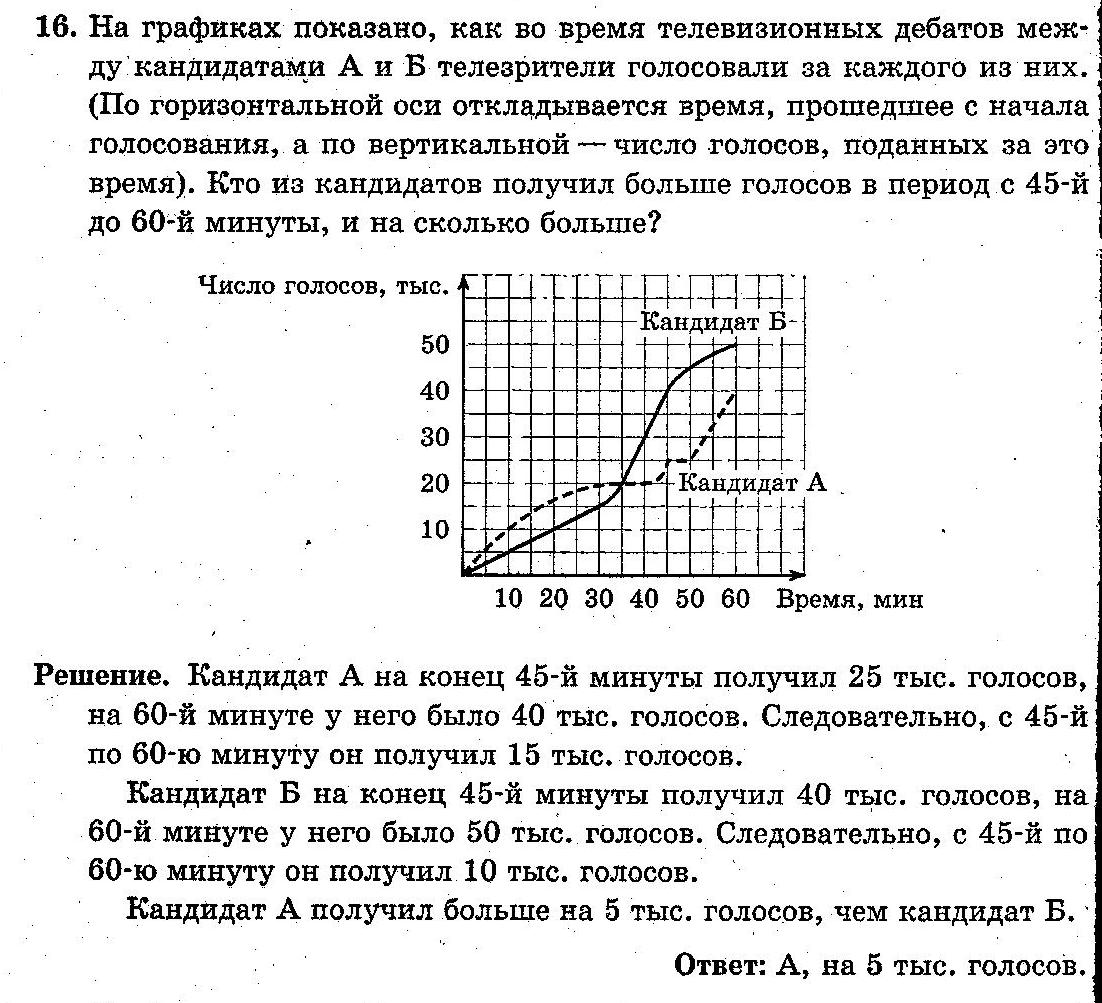
На графике показано, как во время телевизионных дебатов между кандидатами А и Б телезрители голосовали за каждого из них. (По горизонтальной оси откладывается время, прошедшее с начала голосования, а по вертикальной – число голосов, поданных за это время). Кто из кандидатов получил больше голосов в период с 45-ой до 60-й минуты, и на сколько больше?
Решение: Кандидат А на конец 45-й минуты получил 25 тыс. голосов, на 60-й минуте у него было 40 тыс. голосов. Следовательно, с 45-й по 60-ю минуту он получил 15 тыс. голосов. Кандидат Б на конец 45-й минуты получил 40 тыс. голосов, на 60-й минуте у него было 50 тыс. голосов. Следовательно, с 45-й по 60-ю минуту он получил 10 тыс. голосов. Кандидат А получил больше на 5 тыс. голосов, чем кандидат. Ответ: 5000 |
,
с помощью которого требуется перечислить
основные свойства этой функции или
найти соответствующие значения
аргумента или функции..