
- •Тема 13 Решение линейных неравенств с одной переменной
- •Тема 14 Решение квадратного неравенства с опорой на готовый график квадратичной функции
- •Тема 15 Соотнесение графика квадратичной функции с формулой
- •Тема 16 Чтение графика реальной зависимости
- •Тема 17 Решение уравнения третьей степени разложением на множители
- •Тема 18 Решение линейного неравенства с одной переменной с использованием сравнения квадратного корня с рациональным числом
- •Тема 19 Решение задачи с использованием формулы n-го члена геометрической прогрессии .
- •Тема 20 Аналитическая запись кусочно-заданной функции по ее графику
- •Тема 21 Решение текстовых задач
Тема 13 Решение линейных неравенств с одной переменной
Теория |
Практика |
Основная идея решения неравенства состоит в следующем: мы заменяем данное неравенство другим, но равносильным данному. Такие замены осуществляются на основе следующих утверждений:
Если обе части неравенства с переменной умножить или разделить на одно и тоже отрицательное число, заменив при этом знак неравенства на противоположный, то получится неравенство равносильное данному. |
1.Решить
неравенство:
Решение.
Согласно утверждению 1, получим:
Ответ: .
2.
Решите неравенство:
Решение. 1) Решим неравенство методом интервалов. Найдем нули функций, стоящих в числителе и знаменателе:
2)
Отметим на числовой прямой точки:
Определим
знак дроби на каждом промежутке и
выберем те из них, где дробь отрицательна.
Множество решений неравенства состоит
из интервала и
|
Тема 14 Решение квадратного неравенства с опорой на готовый график квадратичной функции
Теория и практика |
||
|
|
|
Если
О |
Если , то , - корни О |
|
Если
О |
Если
О |
|
Если
О |
Е Ответ: |
|
П
Ответ:
|
||
,
|
, |
|
Е Ответ:
|
Если , то , - корни О
|
|
Если , то - корень О |
Если , то - корень О |
|
Если , то корней нет О |
Если , то корней нет О |
|
П Рассмотрим
Ответ: . |
|
|

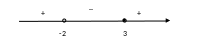
 твет:
твет:
 твет:
твет:
 твет:
твет:
 твет:
твет:
 твет:
твет:
 сли
,
то корней нет
сли
,
то корней нет ример:
ример:
 сли
,
то
,
- корни
сли
,
то
,
- корни твет:
твет:
 твет:
твет:
 твет:
твет:
 твет:
твет:
 твет:
твет:
 ример:
ример: