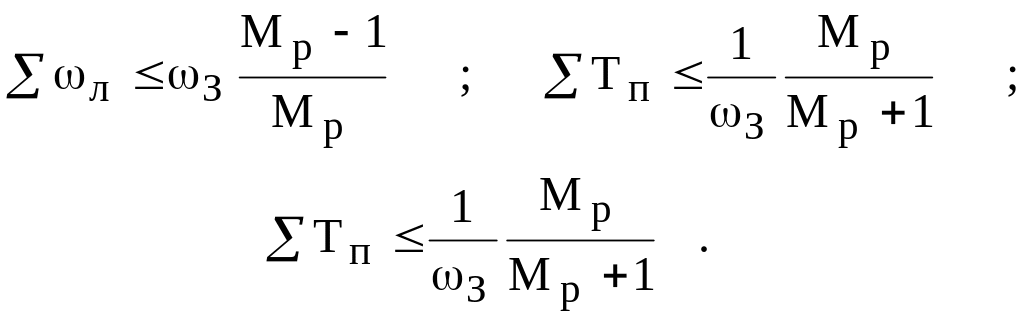6 Методичні вказівки до синтезу бажаної лачх розімкнутої системи

Синтез САК звичайно включає:

1. Попередній синтез бажаної ЛАЧХ, у результаті якого визначаються вимоги до низькочастотної, середньочастотної і високочастотної ЛАЧХ.

2. Синтез коригувальних ланок, який складається із визначення їх ЛАЧХ, передатних функцій і вибору елементів для реалізації останніх.

Синтез низькочастотних ЛАЧХ здійснюється, виходячи з вимог до системи за точністю, і не викликає труднощів.

Характер високочастотної ЛАЧХ, як правило, приймається з умов отримання найбільш простої коригувальної ланки.

Синтез середньочастотної ЛАЧХ (рис.6.1) складається у визначенні частоти зрізу _З і протяжності середньочастотної ЛАЧХ, нахил якої дорівнює -1 (-20ДБ/ДЕК).

Частота зрізу _З визначається швидкодією системи. Остання може бути задана однієї з трьох величин: t_С - час першого узгодження перехідної функції з усталеним значенням; t_Р - час регулювання; t_М - час досягнення перехідною функцією максимального значення. При її обчисленні можна скористатися такими формулами:

(6.1)

(6.2)

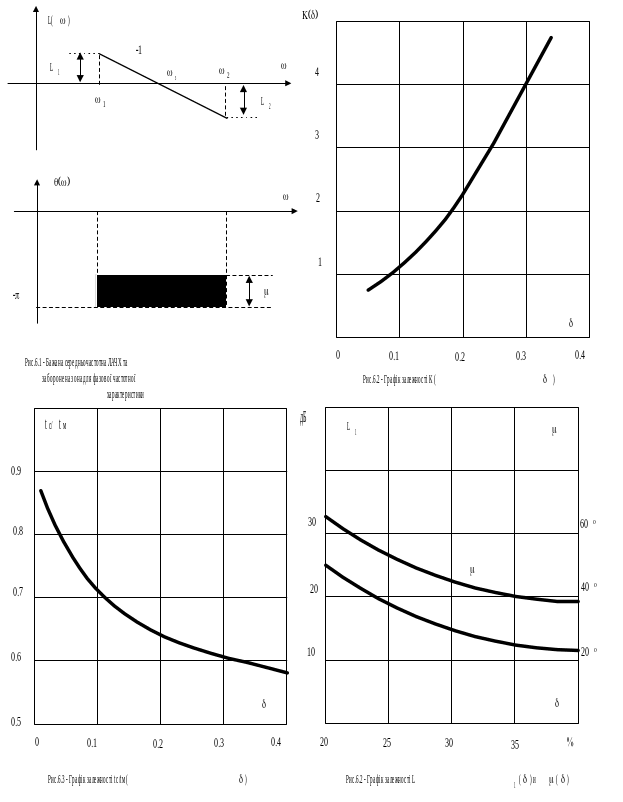
де К(-коефіцієнт, що залежить від заданого перерегулювання (визначається за графіком, поданим на рис.6.2).

Якщо заданий час t_С, то спочатку, скориставшись графіками залежності - рис.6.3, визначається час t_М, а потім частота зрізу з рівняння (6.2).

При визначенні довжини середньочастотної ЛАЧХ звичайно приймають L₁=L₂. Крім того, вимагають, щоб фазова частотна характеристика  не заходила у заборонену зону (на рис.6.5 ця зона заштрихована). Необхідні для визначення довжини середньочастотної ЛАЧХ і забороненої зони для фазової частотної характеристики величини L₁ і  визначаються з графіків, поданих на рис.6.4.

Досвід показує, що довжина середньочастотної ЛАЧХ, що простягається в зону частот >_З, при такому синтезі звичайно велика; реальне перерегулювання в системі, як правило, значно менш заданого. Якщо не враховувати цю обставину, то необхідно рахуватися з тим, що формування протяжної ділянки середньочастотної ЛАЧХ в зоні >_З звичайно важко через необхідність реалізації складних коригувальних ланок.

У цьому зв'язку після попереднього вибору бажаної ЛАЧХ і аналізу можливості реалізації коригувальних ланок треба вносити корективи в характер бажаної ЛАЧХ.

При цьому виникає необхідність рішення таких задач: при яких параметрах більш простої коригувальної ланки, а отже, при якій скоригованій бажаній ЛАЧХ можна задовільнити заданим показникам якості.

Характер розв'язуваних задач залежить від їх постановки. Перед тим , як ознайомитися з деякими з них, умовимося , що частоти сполучення бажаної ЛАЧХ ліворуч частоти зрізу _З називаємо лівими _Л, а праворуч частоти _З - правими _П.

Найбільш поширеними є задачі в таких постановах:

1. При заданій швидкодії (частоті зрізу _З) і заданому перерегулюванні  визначити припустимо мінімально можливі значення правих частот сполучення, при яких задовольняються задані показники якості системи.

2. При заданому перерегулюванні  і заданих правих частотах сполучення _П визначити частоту зрізу _З, при якій забезпечується максимальна швидкодія, і значення лівих частот сполучення.

3. При заданих частотах сполучення (_Л і _П) визначити частоту зрізу _З, при якій буде максимальна швидкодія при мінімальному значенні перерегулювання.

Приємні результати дає методика синтезу за мінімумом резонансного максимуму Мр амплітудно-частотної характеристики замкненої системи (АЧХ). Ця методика, запропонована Экслбі і розвинута в роботі /7/, полягає в суміщенні резонансної частоти _Р , при якій досягається максимум АЧХ замкненої системи Мр, із частотою экстремума фазової частотної характеристики розімкненої системи.

У роботі /7/ показано, що таке суміщення дає можливість при заданих частотах сполучення або частотах зрізу синтезувати систему з мінімальним значенням Мр (мінімальним перерегулюванням і коливанням перехідних процесів) і, навпаки, при заданому значенні Мр (заданому перерегулюванні) забезпечити максимальну швидкодію.

Для практичного застосування розглянутого критерію достатньо знати, що мінімальне значення Мр визначається з рівняння

, (6.3)

а необхідна частота зрізу

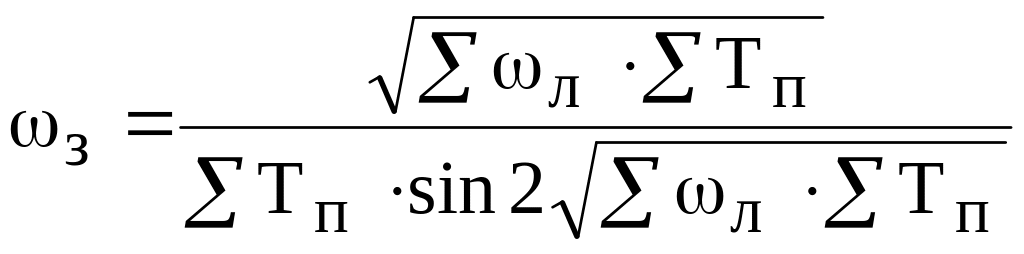, (6.4)

де Т_П - алгебраїчна сума величин, обернених частотам сполучення, що знаходяться справа від частоти _З (додатні члени відповідають частотам сполучення, при яких відбувається збільшення нахилу ЛАЧХ);

_Л - алгебраїчна сума частот сполучення, що знаходяться ліворуч від частоти зрізу _З (додатні члени відповідають частотам сполучення, при яких відбувається зменшення нахилу ЛАЧХ).

Якщо в системі є коливальні ланки з передатною функцією

, або форсувальні ланки другого порядку з передатною функцією, , то частота сполучення поділяється на 2 (при визначенні правих частот сполучення) і помножується на 2 (при визначенні лівих _Л).

Приведене формулювання справедливе, якщо всі частоти сполучення різні. Якщо ж нахил ЛАЧХ обумовлен двома (трьома) аперіодичними ланками або форсувальними ланками першого порядку, то кількість відповідних частот сполучення подвоюється (потроюється).

Спільне рішення рівнянь (6.3) і (6.4) дає

, (6.5)

. (6.6)

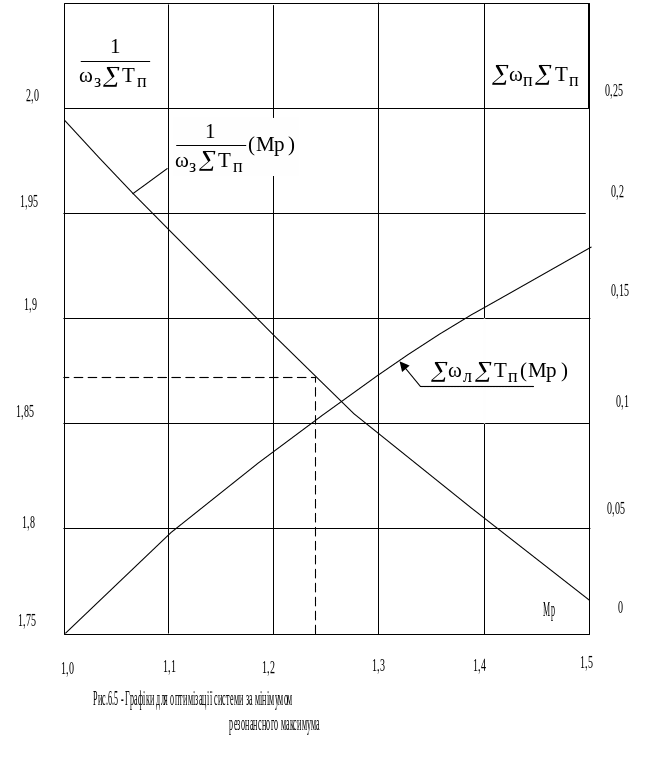
Графіки залежностей і , побудовані за рівняннями (6.5) і (6.6), приведені на рис.6.5. Користуючись графіками , можна легко визначити необхідні параметри бажаної ЛАЧХ.

Трудність при оптимізації систем за мінімумом резонансного максимуму полягає в складності пошуку точних залежностей перерегулювання  від величини Мр.

Тому на практиці використовують спрощену формулу

(6.7 )

Поставлені раніш задачі можуть бути сформульовані наступним способом.

Задача №1.

Задані : _З,  і характер ЛАЧХ.

Визначити: Т_П і _Л

Рішення

З формули (6.8)

визначається необхідне значення Мр.

По величині Мр із графіків (рис.6.5) визначається значення і , і далі параметри, що шукають:

.

Задача №2.

Задані : (а отже, Мр), Т_П і характер ЛАЧХ.

Визначити: _З та _Л

Рішення

По величині Мр із графіків на рис.6.5 визначають і .

Далі обчислюють

Задача №3.

Задані : _Л , Т_П і характер ЛАЧХ.

Визначити: _З і мінімальне значення Мр.

Рішення

По заданим _,_Л і Т_П визначають їх множення , а потім із графіків знаходять Мр.

По знайденому значенню Мр із графіків рис.6.5 визначають і відповідно .

При рішенні названих задач можливо застосування також таких залежностей, що установлюють взаємозв'язок між резонансним максимумом Мр і необхідними для його виконання параметрами /1,3/: