лекции по УГФС (7-12) / Лекция 9

Лекция 9

Эквивалентная схема выходной цепи ГВВ при разных режимах работы по напряжённости. Амплитудно- и фазо-частотная характеристики (АЧХ и ФЧХ) ГВВ.

В области недонапряжённого вплоть до критического режима работы ГВВ при кусочно-линейной аппроксимации статических ВАХ амплитуда первой гармонической составляющей выходного тока АЭ, например, анодного тока лампы (аналогично коллекторного тока транзистора), определяется соотношением (6.10)

, (9.1)

которое, учитывая, что , можно представить в виде

. (9.2)

Из (9.2) следует

, (9.3)

где учтено - статический коэффициент усиления лампы; - приведенное (по первой гармонике в данном случае) внутреннее сопротивление лампы; - коэффициент приведения.

В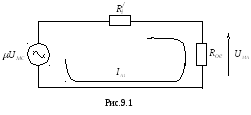 ыражение (9.3) соответствует электрической схеме рис.9.1, которая может рассматриваться как эквивалентная схема выходной цепи ГВВ в области недонапряжённого вплоть до критического режима работы генератора.

В лекции 8 отмечалось, что при работе генератора на комплексную нагрузку, каковой является, например, ненастроенный параллельный колебательный контур в выходной цепи АЭ ГВВ, амплитуда первой гармоники выходного тока АЭ и в этом случае может быть определена как амплитуда первой гармонической составляющей косинусоидального импульса соответствующей амплитуды и такой же ширины, как и при активной нагрузке. Это позволяет считать схему, подобную рис.9.1, справедливой и при комплексной нагрузке , как показано на рис.9.2, где

- соответственно, активная и реактивная составляющие сопротивления нагрузки в последовательной схеме замещения.

Согласно схеме рис.9.2 комплексная амплитуда первой гармоники анодного (аналогично коллекторного) тока

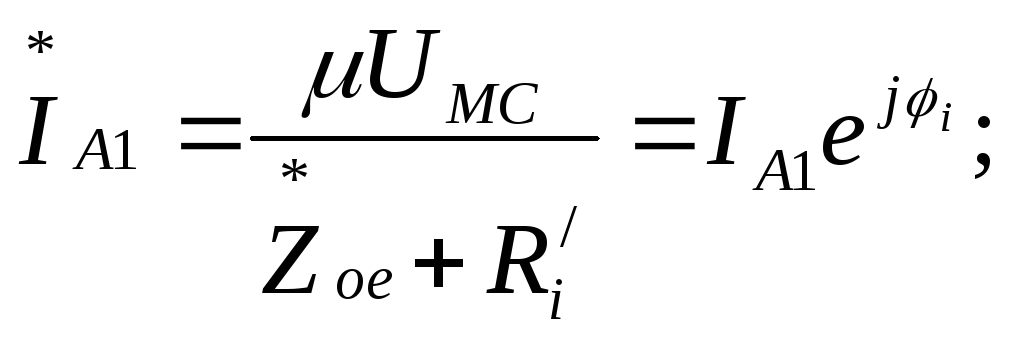
комплексная амплитуда колебательного напряжения на аноде (коллекторе)

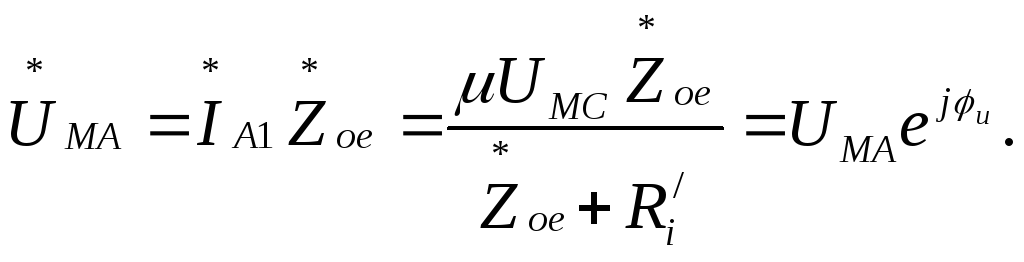
Последние выражения позволяют определить амплитудные и фазовые характеристики ГВВ, соответственно, по току и напряжению.

Амплитудно-частотная характеристика (АЧХ) по току

(*)

фазо-частотная характеристика (ФЧХ) по току

(9.4)

АЧХ по напряжению

(**)

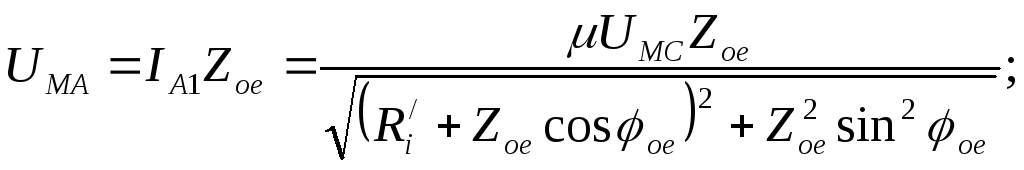ФЧХ по напряжению

Если то есть D = 0, то , а , что отмечалось в лекции 8. При , а .

Если в качестве нагрузки используется параллельный колебательный контур с полным включением, то в окрестности резонансной частоты его сопротивление описывается выражением

согласно которому АЧХ и ФЧХ такого контура

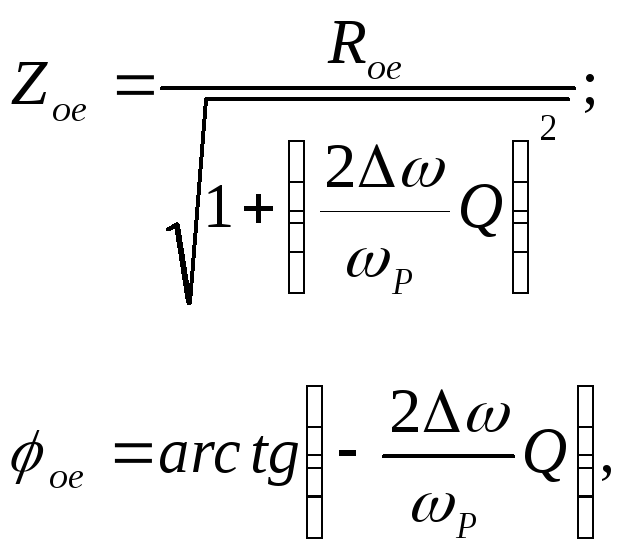
где - расстройка относительно резонансной частоты контура ; - частота входного сигнала; - эквивалентное сопротивление контура на резонансной частоте; Q - добротность контура.

Н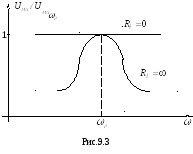 а рис.9.3 показаны относительные АЧХ ГВВ по напряжению для крайних случаев: и при использовании в качестве нагрузки в выходной цепи ГВВ параллельного колебательного контура.

При АЧХ генератора по напряжению определяется АЧХ параллельного колебательного контура , а при АЧХ генератора по напряжению представляет прямую линию, параллельную оси частот. В этом случае выходное напряжение генератора не зависит от нагрузки, соответственно и от частоты настройки контура, и определяется напряжением эквивалентного генератора . Таким образом, чем меньше , тем сильнее АЧХ генератора по напряжению отличается от АЧХ параллельного колебательного контура, используемого в качестве нагрузки АЭ ГВВ. В общем случае АЧХ ГВВ шире, чем АЧХ параллельного колебательного контура по такому же уровню.¹ Это необходимо учитывать при определении частотных искажений в ГВВ – усилителях широкополосных сигналов, в том числе, например, модулированных сигналов.

Если , то значение  может быть не определено и приведенными выше выражениями для АЧХ и ФЧХ, соответствующими эквивалентной схеме рис. 9.2, пользоваться неудобно. В этом случае для определения АЧХ и ФЧХ ГВВ удобнее воспользоваться выражениями, соответствующими эквивалентной схеме выходной цепи ГВВ, представленной на рис.9.4.

Схема рис.9.4 получается из схемы рис. 9.2 путём преобразования генератора напряжения с внутренним сопротивлением в генератор тока величиной с внутренним сопротивлением , где - средняя (по первой гармонике) крутизна выходного тока АЭ.²

Эквивалентная схема рис.9.4 для случая настроенного контура следует также непосредственно из выражения (9.2), согласно которому

откуда

что соответствует электрической схеме рис.9.4 для случая настроенного контура . Очевидно, для случая настроенного контура получающаяся эквивалентная схема выходной цепи ГВВ рис.9.4 соответствует схеме рис.9.1 при преобразовании генератора тока величиной с внутренним сопротивлением в эквивалентный генератор напряжения величиной с внутренним сопротивлением .

Согласно схеме рис.9.4 в общем случае комплексной нагрузки в выходной цепи АЭ ГВВ

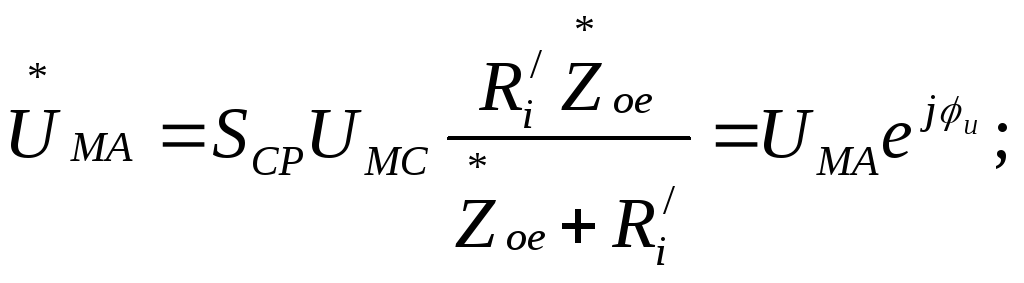(9.5)

откуда АЧХ генератора по напряжению

(***)

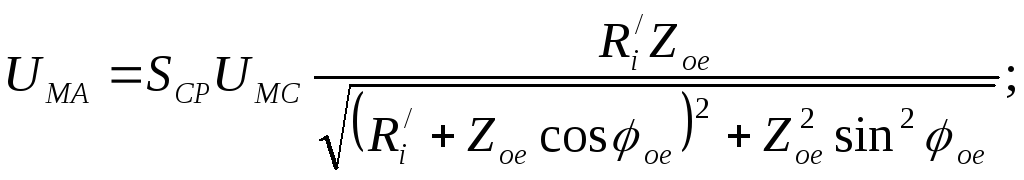АЧХ генератора по току

(****)

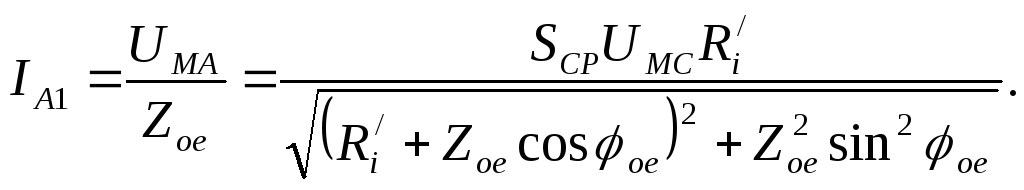Обратим внимание, что выражения (***), (****) соответствуют выражениям (*) и (**), в которых соответствует .

Из (9.5) видно, что АЧХ ГВВ по напряжению может рассматриваться как АЧХ подключенного к АЭ параллельного колебательного контура, зашунтированного приведенным внутренним сопротивлением АЭ. Эквивалентное сопротивление такого контура на резонансной частоте

.

Так как реактивные параметры контура ёмкость и индуктивность не изменились, то уменьшение эквивалентного сопротивления контура на резонансной частоте свидетельствует об уменьшении добротности контура и, соответственно, о расширении его полосы пропускания. Таким образом, АЧХ системы: АЭ – контур может рассматриваться как АЧХ эквивалентного контура с такими же реактивностями, но с меньшим эквивалентным сопротивлением на резонансной частоте. Если D = 0, то , соответственно и . Шунтирования контура в этом случае нет, и АЧХ ГВВ по напряжению совпадает с АЧХ контура , что отмечалось выше.

Н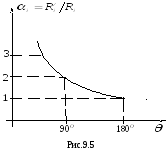 а рис.9.5 показан график зависимости .

Если , то . В общем случае при , то есть , как следует из (9.4), имеет противоположный знак, что обусловливает меньшую величину по сравнению с величиной , что отмечалось в лекции 8. Напомним, что и определяют фазовые сдвиги первой гармоники выходного тока и колебательного напряжения на выходе АЭ относительно сигнала возбуждения. Что касается сдвига по фазе между первой гармоникой выходного тока и колебательным напряжением, то он равен .

П ри работе генератора в перенапряжённом режиме, когда , а , где - остаточное напряжение на аноде (на коллекторе) в критическом режиме, можно считать, что амплитуда колебательного напряжения остаётся практически неизменной и равной . Очевидно, чем больше крутизна линии критических режимов (она же линия насыщения в транзисторном ГВВ), тем с большим основанием можно считать справедливым последнее утверждение. В этом случае для выходной цепи ГВВ применима эквивалентная схема рис. 9.6.

На рис.9.7 показаны ДХ анодного тока при работе лампового ГВВ в перенапряжённом режиме на комплексную нагрузку в анодной цепи, которые могут быть построены с использованием соотношений (8.3) и семейства статических ВАХ анодного тока. В зависимости от степени расстройки контура наклон ДХ и расширение эллипса в зоне основной области характеристик будет несколько изменяться, но амплитуда колебательного напряжения будет мало изменяться, пока режим будет оставаться перенапряжённым.

Таким образом, при работе ГВВ в перенапряжённом режиме АЧХ генератора по напряжению практически не зависит от величины сопротивления нагрузки в выходной цепи и характера этого сопротивления. АЧХ генератора по току, напротив, зависит от величины и характера сопротивления нагрузки в выходной цепи и определяется из выражения

.

АЧХ по току имеет обратную зависимость

Минимальное значение мгновенного тока в области перенапряжённого режима (точка 1 на рис.9.7), по-прежнему, соответствует минимальному мгновенному напряжению на аноде

,

которое, согласно (8.3), имеет место при .

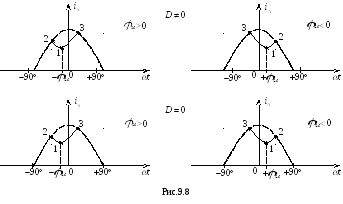
На рис.9.8 показаны формы импульсов анодного тока, соответствующие ДХ рис.9.7.

Очевидно, за счёт асимметричного расположения провала в импульсах выходного тока АЭ относительно периода сигнала возбуждения ωt = 0; 2π и т.д. при работе на комплексную нагрузку в перенапряжённом режиме первая гармоническая составляющая выходного тока получает свой фазовый сдвиг даже при D = 0. В недонапряжённом режиме этого нет.

Рассмотренные эквивалентные схемы выходной цепи ГВВ пригодны для расчёта частотных (амплитудных и фазовых) характеристик генератора, но не пригодны для анализа оптимальных условий его работы, так как ГВВ по природе своей является сугубо нелинейным устройством: независимо от режима параметры генератора зависят, в той или иной степени, от сопротивления нагрузки. Поэтому, если, например, исходить из эквивалентной схемы рис.9.6, то, как кажется, чем меньше , тем больше колебательная мощность

Однако, коэффициент использования напряжения источника питания анода (коллектора) ξ существенно зависит от и при малых значениях не может быть обеспечено большое значение ξ.

Точно также, если обратиться, например, к эквивалентной схеме рис.9.1, то, казалось бы, как известно из курса теории линейных электрических цепей,³ оптимальное сопротивление нагрузки, при которой обеспечивается максимальная мощность, будет

В то же время, как показано в лекции 6, оптимальное значение сопротивления нагрузки

.

Только при имеет место совпадение значений и При при .

Кроме того, в схеме рис.9.1 параметры эквивалентного генератора: его напряжение и внутреннее (выходное) сопротивление зависят от , так как от зависит θ:

и для сохранения θ с изменением потребуется изменить и .

Действительно, если рассмотреть даже случай , то из выражения для , учитывая, что следует

Так как и значение последнего должно поддерживаться неизменным, следовательно, , то на основании последнего выражения получаем

то есть, и являются функциями , значит и .

Только при зависимость θ от практически исчезает, но соответствует , и если считать , то при этом пропадает справедливость самой схемы, так как при режим генератора будет перенапряжённым, а для него схема рис.9.1 уже недействительна.

Зависимость параметров рассмотренных эквивалентных схем выходной цепи ГВВ от сопротивления нагрузки указывает на тот факт, что возможно видоизменение схем.

В частности, например, для области недонапряжённого вплоть до критического режима может быть предложена эквивалентная схема выходной цепи ГВВ, отличающаяся от схемы рис.9.1.

Если обратиться к выражению (9.1) и принять во внимание, что

то получаем

откуда находим, учитывая, что

Последнему выражению соответствует электрическая схема рис.9.9.

Как видно, схема рис.9.9 отличается от схемы рис.9.1. В схеме рис.9.9 внутреннее (выходное) сопротивление эквивалентного генератора совпадает с оптимальным сопротивлением нагрузки , но и в этой схеме необходимо иметь в виду, что зависит от , так как зависит от через зависимость θ от .

Очевидно, вместо схемы рис.9.9 с эквивалентным генератором напряжения может быть предложена схема рис.9.10 с эквивалентным генератором тока .

Если в схемах рис.9.9 и рис.9.10 заменить на , то схемы можно использовать для определения частотных характеристик генератора. В частности, на основании схемы рис.9.9 для АЧХ и ФЧХ генератора по току получаем:⁴

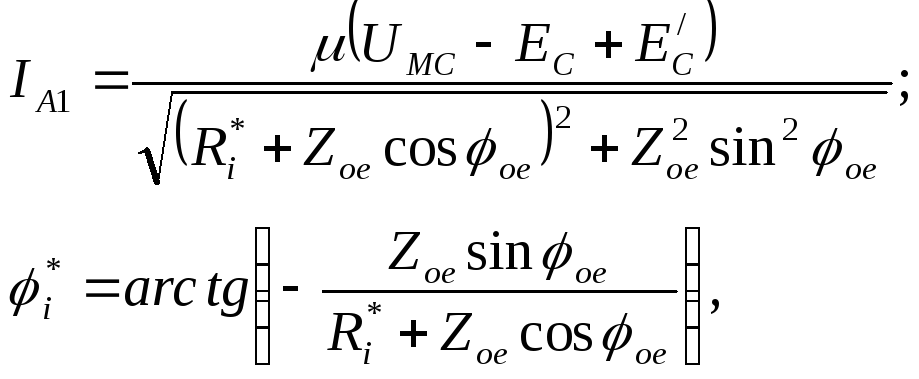
при этом комплексная амплитуда первой гармоники анодного тока

Соответственно, АЧХ и ФЧХ по напряжению

Очевидно, несмотря на то, что выражения для АЧХ по току, соответственно, и выражения для АЧХ по напряжению, получаемые на основании схем рис.9.9 и рис.9.10, отличаются несколько по виду от полученных на основании схем рис.9.2 и рис.9.4, сами АЧХ по форме не должны отличаться. Что касается ФЧХ, то они будут отличаться, так как отличаются опорные напряжения в выражениях, относительно которых определяются фазы выходного тока и колебательного напряжения. В схемах рис.9.2 и рис.9.4 таким напряжением является напряжение возбуждения, а в схемах рис.9.9 и рис.9.10 эквивалентное напряжение . При этом также отличаются внутренние (выходные) сопротивления эквивалентных генераторов и . Что касается сдвига по фазе между первой гармоникой выходного тока и выходным (колебательным) напряжением, то при использовании любой эквивалентной схемы выходной цепи ГВВ этот сдвиг по фазе равен . Так как практический интерес представляет сдвиг по фазе между входным и выходным сигналами, то для расчёта ФЧХ следует использовать выражения, вытекающие из рассмотрения схем рис.9.2 и рис.9.4.

Схема рис.9.9 позволяет легко проследить изменение всех характеристик генератора по выходной цепи от сопротивления нагрузки, нижнего угла отсечки, напряжений питания и возбуждения.

Действительно, напряжение эквивалентного генератора в схеме рис.9.9 можно представить как

и если обозначить где а - коэффициент пропорциональности, то

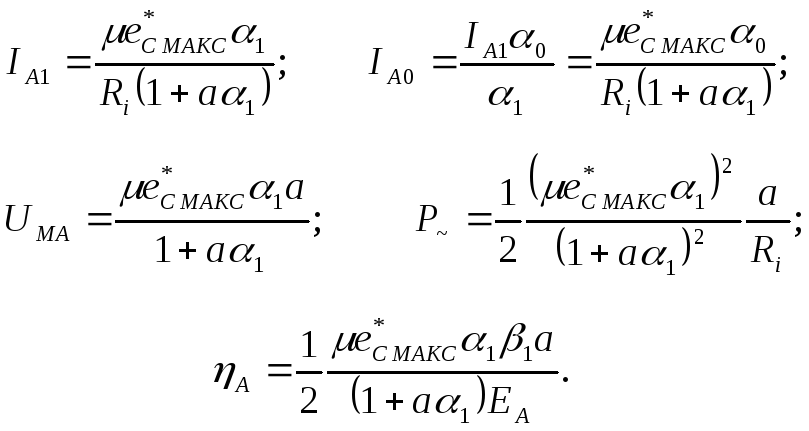
Приведенные соотношения позволяют сравнить, как изменяются основные характеристики генератора при изменении нагрузки и угла нижней отсечки выходного тока θ.

Например, при и при

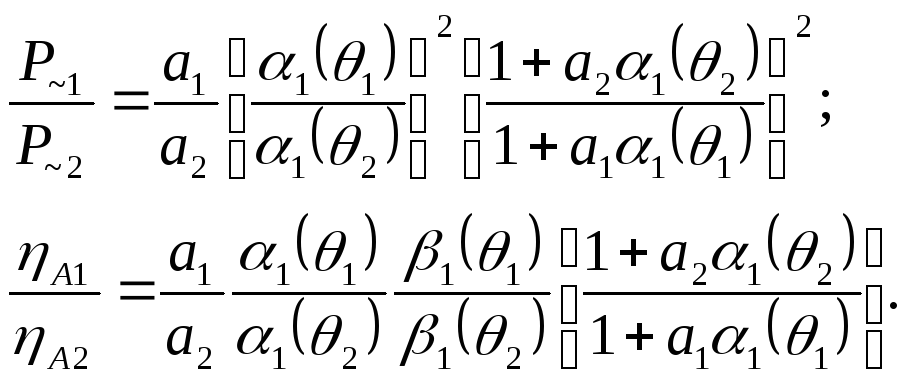
Согласно последним соотношениям при и , что соответствует , и при и , что также соответствует ,

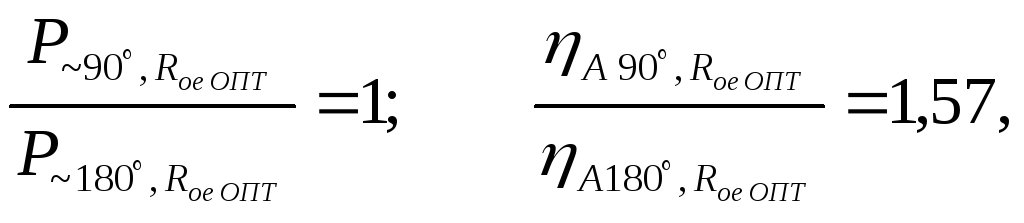
то есть при оптимальном сопротивлении нагрузки при и колебательная мощность одинакова, но КПД анодной (коллекторной) цепи при существенно выше, чем при .

Если принять и , то есть , и , но , то есть =1, то

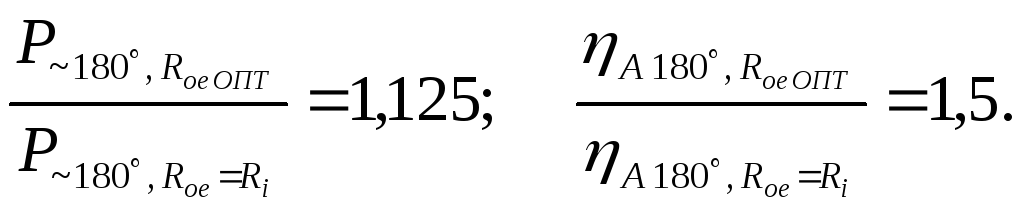
Аналогично получаем

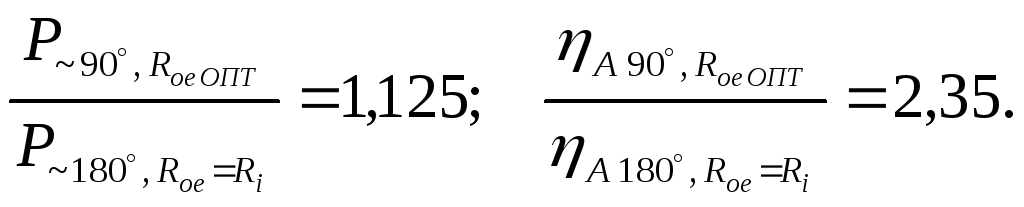
При работе генератора с и колебательная мощность возрастает, примерно, на 12%, а КПД анодной (коллекторной) цепи увеличивается на 50% по сравнению с режимом , но . Режим с и более выгоден по всем рассмотренным параметрам.

Если принять и , что соответствует , то

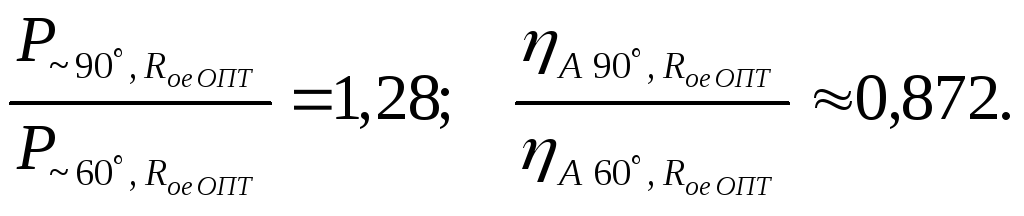
В этом случае по сравнению с и колебательная мощность генератора уменьшается, а КПД анодной (коллекторной) цепи возрастает, но в меньшей степени, чем уменьшается мощность.