Случайные величины

1. Дискретные и непрерывные случайные величины

Понятие случайной величины является основным, неопределяемым понятием ТВ.

Под случайной величиной понимается переменная, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений (какое именно — за­ранее не известно). Это зависит от случая. С любой случайной величиной связывается множество ее значений.

Обозначение случайных величин: X,У, Z

Обозначение множества значений: х₁, х₂,…х_n – Х

Примеры случайных величин:

1. число родившихся детей в течение суток в г. Оренбурге;

2. количество бракованных изделий в данной партии;

3. число произведенных выстрелов до первого попадания;

4. дальность полета артиллерийского снаряда;

5. расход электроэнергии на предприятии за месяц.

Опр. Случайная величина, которая может принимать все значения сплошь из некоторого конечного или бесконечного пространства называется непрерывной.

Опр. Случайная величина, которая может принимать отдельные изолированные значения с определенными вероятностями, называется дискретной случайной величиной (множество ее значений конечное, или бесконечное, но счетное).

Так, в приведенных выше примерах 1-3 имеем дискретные случайные величины (в примерах 1,2 - с конечным множеством значений; в примере 3-е бесконечным, но счетным множест­вом значений); а в примерах 4,5 - непрерывные случайные ве­личины.

2. Закон распределения вероятностей дискретной случайной величины

Рассмотрим 2 случайные величины:

Х – число выпадения герба при однократном бросании монеты {0, 1}.

Y – число выпадения двух очков при однократном бросании кости {0, 1}.

Р(Х>0)= ½

Р(Y>0)= 5/6

Для характеристики случайной величины недостаточно знать только множество ее значений, нужно еще знать вероятности значений, принимаемых случайной величиной

Опр. Законом распределения случайной вели­чины называется всякое соотношение, устанавливающее связь ме­жду возможными значениями случайной величины и соответст­вующими им вероятностями.

Про случайную величину говорят, что она «распределена» по данному закону распределения или «подчинена» этому закону распределения.

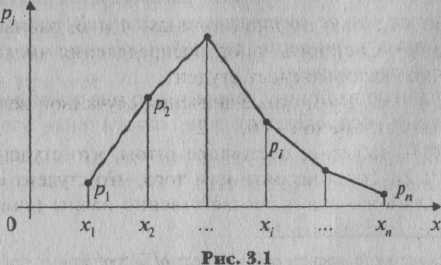
Для дискретной случайной величины закон распре­деления может быть задан в виде таблицы, аналитически (в виде формулы) и графически.

Простейшей формой задания закона распределения дискрет­ной случайной величины Х является таблица (матрица), в которой перечислены в порядке возрастания все возможные значения слу­чайной величины и соответствующие их вероятности, т.е.

х1	х2	…	хi	…	хп
р1	р2	…	Pi	…	рп

X:

или

Такая таблица называется рядом распределения дискретной случайной величины.

События Х=x1, Х=x2,..., Х=х_п, состоящие в том, что в результате испытания случайная величина X примет соответственно значения х1, х2,...,х_п, являются несовместными и единственно возможными (ибо в таблице перечислены все возможные значения случайной величины), т.е. образуют полную группу. Следовательно, сумма их вероятностей равна 1. Таким образом, для любой дискретной случайной величины

(3.1)

(Эта единица как-то распределена между значе­ниями случайной величины, отсюда и термин «распределение»).

Ряд распределения может быть изображен графически, если по оси абсцисс откладывать значения случайной величины, а по оси ординат — соответствующие их вероятности. Соединение полученных точек образует ломаную, называемую многоугольником или полигоном распределения вероятностей.

Задача 1. В лотерее разыгрывается: автомобиль стоимостью 5000 ден. ед., 4 телевизора стоимостью 250 ден. ед., 5 видеомагнитофонов стоимостью 200 ден. ед. Всего продается 1000 билетов по 7 ден. ед. Составить закон распределения чистого выигрыша, полученного участником лотереи, купившим один билет.

Решение. Возможные значения случайной величины X — чистого выигрыша на один билет — равны

0-7 = -7 ден. ед. (если билет не выиграл),

200-7 = 193,

250-7 = 243,

5000-7 = 4993 ден. ед. (если на билет выпал выигрыш соответственно видеомагнитофона, телевизора или автомобиля).

Учитывая, что из 1000 билетов число невыигравших составляет 990, а указанных выигрышей соответственно 5, 4 и I, и, используя классическое определение вероятности, получим:

Р{Х=-7) = 990/1000=0,990; Р(Х=193) =5/1000=0,005;

Р(Х=243) = 4/1000=0,004; Р(Х=4993)= 1/1000=0,001, т.е. ряд распределения

хi	-7	193	243	4993
Pi	0,990	0,005	0,004	0,001