4.5. Движение жидкости в трубах некруглого сечения

Для транспорта капельных жидкостей и газов иногда используют трубопроводы некруглого сечения: овальной, прямоугольной формы. В таких трубах возникают так называемые вторичные течения (рис. 4.13), которые можно наблюдать при подкрашивании потока.

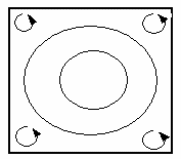
Рис. 4.13. Движение жидкости в трубопроводах некруглого сечения

Вторичные течения происходят в плоскости поперечного сечения трубы: частицы жидкости движутся при этом от центра трубы к углам. Накладываясь на продольные движения, вторичные течения непрерывно переносят частицы жидкости в угловые области, где наблюдаются сравнительно высокие продольные скорости. Гидравлическое сопротивление таких труб выше, чем сопротивление аналогичных круглых труб одинакового поперечного сечения.

При турбулентном движении жидкости коэффициенты гидравлического трения соответствуют коэффициентам для круглых труб, а увеличение сопротивления учитывается тем, что труба некруглого сечения приводится к трубе круглой соответствующего диаметра. Для этого применяется эквивалентный диаметр

,

(4.13)

где – гидравлический радиус.

,

(4.14)

где S – площадь сечения трубопровода; χ – смоченный периметр.

Например, для прямоугольного трубопровода со сторонами a и b:

,

для квадратного сечения:

,

для равнобедренного треугольного сечения со сторонами a и высотой h

.

4.6. Местные гидравлические сопротивления

Местные сопротивления вызываются фасонными частями, арматурой, другим оборудованием трубопроводных сетей, которые изменяют величину или направление скорости движения жидкости на отдельных участках, что всегда связано с появлением дополнительных потерь напора.

Потери напора на местных сопротивлениях определяются по формуле Вейсбаха

(4.15)

где – коэффициент местного сопротивления, который зависит от вида сопротивления и определяется опытным путем.

Основные виды местных потерь напора можно условно разделить на следующие группы:

• потери, связанные с изменением живого сечения потока (резкое или постепенное расширение и сужение потока);

• потери, вызванные изменением направления потока, его поворотом (поворот трубы);

• потери, связанные с протеканием жидкости через арматуру различного типа (вентили, краны, клапаны, сетки);

• потери, возникшие вследствие отделения одной части потока от другой или слияния двух потоков (тройники, крестовины и т.д.).

Рассмотрим некоторые виды местных сопротивлений.

Рис. 4.14. Резкое расширение трубопровода

Резкое расширение трубопровода.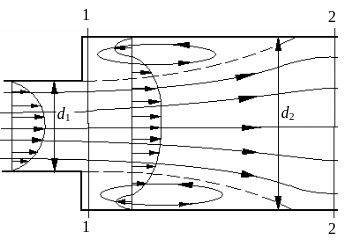

Как показывают наблюдения, поток, выходящий из узкой трубы, отрывается от стенок и дальше движется в виде струи, отделенной от остальной жидкости поверхностью раздела (см. рис. 4.14). На поверхности раздела возникают вихри, которые отрываются и переносятся далее транзитным потоком. Между транзитным потоком и водоворотной зоной происходит массообмен, но он незначителен. Струя постепенно расширяется и на некотором расстоянии от начала расширения заполняет все сечение трубы. Вследствие отрыва потока и связанного с этим вихреобразования на участке трубы между сечениями 1-1 и 2-2 наблюдаются значительные потери напора.

Если принять ряд допущений, то теоретически можно доказать, что потери напора при резком расширении

– формула Борда,

где и – средние скорости в трубе до расширения и после. Эту формулу можно привести к другому виду:

.

Если принять

,

(4.16)

Рис. 4.15. Постепенное расширение трубопровода

коэффициент местного сопротивления при резком расширении, то формула Борда принимает следующий вид:

.

В случае присоединения трубы к резервуару можно принять = , тогда .

Постепенное расширение.

Если расширение происходит постепенно (см. рис. 4.15), то потери напора значительно уменьшаются. При течении жидкости в диффузоре скорость потока постепенно уменьшается, уменьшается кинетическая энергия частиц, но увеличивается градиент давления. При некоторых значениях угла расширения α частицы у стенки не могут преодолеть увеличивающееся давление и останавливаются. При дальнейшем увеличении угла частицы жидкости могут двигаться против основного потока, как при резком расширении. Происходит отрыв основного потока от стенок и вихреобразование. Интенсивность этих явлений возрастает с увеличением угла α и степенью расширения .

Потерю напора в диффузоре можно условно рассматривать как сумму потерь на трение и расширение. При небольших углах α возрастают потери по длине, а сопротивление на расширение становится минимальным. При больших углах α наоборот возрастает сопротивление на расширение. Коэффициент сопротивления диффузора можно определить по следующей формуле

,

(4.17)

Рис. 4.16. Внезапное сужение трубопровода

где k – коэффициент смягчения, который зависит от угла α, и его значения приводятся в справочниках

.

Внезапное сужение.

При внезапном сужении потока (см. рис. 4.16) также образуются водоворотные зоны в результате отрыва от стенок основного потока, но они значительно меньше, чем при резком расширении трубы, поэтому и потери напора значительно меньше. Коэффициент местного сопротивления на внезапное сужение потока можно определить по формуле

, где .

(4.18)

В случае присоединения трубы к резервуару можно принять = , тогда .

Постепенное сужение (конфузор).

Величина сопротивления конфузора будет зависеть от угла конусности конфузора θ. Коэффициент сопротивления можно определить по формуле

,

Рис. 4.17. Плавный поворот трубопровода

где , приводится в справочниках.

Поворот трубы (колено).

В результате искривления потока на вогнутой стороне внутренней поверхности трубы давление больше, чем на выпуклой. В связи с этим жидкость движется с различной скоростью, что способствует отрыву от стенок пограничного слоя и потерям напора (см. рис. 4.17). Величина коэффициента местного сопротивления зависит от угла поворота θ, радиуса поворота R, формы поперечного сечения и приводится в справочниках. Для круглого сечения трубы при θ = 90º. коэффициент сопротивления можно определить по формуле

.

(4.18)

Рис. 4.18. Вентиль

Другие виды местных сопротивлений.

Коэффициенты местных сопротивлений для большинства сопротивлений приводятся в справочниках, их величина зависит от конструкции. Для ориентировочных расчетов можно пользоваться следующими коэффициентами местного сопротивления:

• задвижка при полном открытии – 0,15;

• вход в трубу при острых кромках – 0,5;

• вентиль с косым затвором при полном открытии (рис. 4.18) – 3;

• симметричный тройник – 1,5.