3 Построение кривой свободной поверхности потока

Неравномерное установившееся движение воды в каналах характеризуется изменением вдоль потока основных его характеристик, т.е. давление и скорость изменяются вдоль потока, в связи с изменением глубины. Уклоны дна, свободной поверхности и гидравлический уклон не равны между собой. Вертикальное сечение призматического русла не изменяется по длине потока, поэтому площадь живого сечения потока зависит только от глубины.

В одних случаях неравномерное движение возникает за счет изменения уклона, в других – как результат деформации формы живого сечения потока. Это, как правило, вызвано строительством в русле каких либо гидротехнических сооружений. Постоянной гидравлической характеристикой потока при неравномерном установившемся движении остается величина расхода Q, м³/с . Как правило, движение в открытых руслах происходят в доквадратичной области гидравлических сопротивлений.

Построение кривой свободной поверхности потока, т.е. кривой пересечения вертикальной продольной плоскости со свободной поверхностью потока, представляет большой практический интерес. Построив кривую можно найти глубины воды в канале в различных его сечениях. Зная глубины воды, можно решить вопрос об определении площади вертикального сечения потока и пропускной способности.

Неравномерное установившееся движение потока описывается дифференциальным уравнением

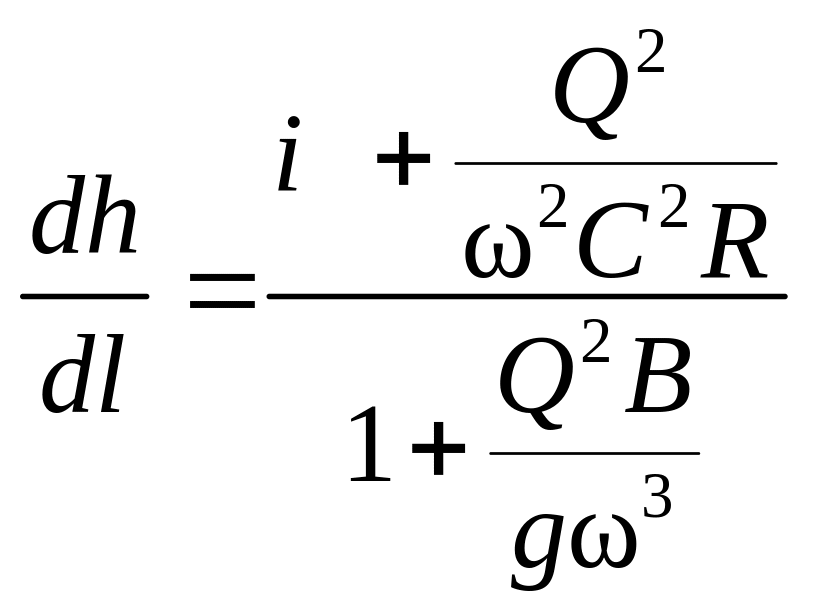. (1)

где	i	–	продольный уклон дна канала;
	Q	–	расчетный расход воды, м3/с;
	ω	–	площадь поперечного сечения, м2;
	g	–	ускорение силы тяжести, м2/с;
	С	–	коэффициент Шези,
	R	–	гидравлический радиус, м;
	B	–	ширина потока по верху, м.

Решение уравнения (1) предложено Б. А. Бахметевым

, (2)

где l	–	длина, м
h0	–	нормальная глубина, м;
i	–	уклон;
η1, η2	–	относительные глубины соответственно в первом и во втором сечениях, м;
jср	–
Б(η1), Б(η2)	–	функции Бахметева, определяются в зависимости от относительных глубин η1, η2 и гидравлического показателя русла x.

При решении задачи о построении кривой свободной поверхности методом Б.А. Бахметева весь расчет удобно разбить на отдельные пункты и пояснить их выполнение. Для этого необходимо определить нормальную и критическую глубину; критический уклон; относительные глубины; гидравлический показатель русла; относительные глубины; коэффициент пропорциональности; функции Бахметева. Затем рассчитать зависимость между длиной участка и глубинами его ограничивающими, согласно уравнению (2) и построить линию свободной поверхности.