1. Робота магнітного поля по переміщенню струму. Циркуляція вектора магнітної індукції.

-- На провідник зі струмом у магнітному полі діє сила Ампера. Якщо провідник не закріплено, то під впливом сили Ампера він переміщуватиметься у магнітному полі.

Обчислимо роботу dA, виконану силою Ампера при переміщенні елемента dl провідника зі струмом І у магнітному полі (рис. 113).

Елемент провідника переміщується в напрямку сили  , яка діє на нього. Робота dА дорівнює:

.

За законом Ампера

.

Тоді

.

Сила   і переміщення   напрямлені перпендикулярно до елемента провідника  .

Добуток   – площа поверхні, яка описана елементом провідника dl при його переміщенні на dx.

З рис. 113 видно, що   – проекція вектора   на напрямок нормалі   до площини dS.

Добуток   – магнітний потік крізь поверхню dS. Тоді

.

Вважаючи силу струму сталою і, інтегруючи цей вираз, отримаємо

.

-- Возьмем контур l (рис. 2.8), охватывающий прямой ток I, и вычислим для него циркуляцию вектора магнитной индукции   , т.е.   .

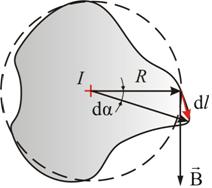
Рис. 2.8

      Вначале рассмотрим случай, когда контур лежит в плоскости перпендикулярно потоку (ток I направлен за чертеж). В каждой точке контура вектор    направлен по касательной к окружности, проходящей через эту точку (линии    прямого тока – окружности).

      Воспользуемся свойствами скалярного произведения векторов.

          где    – проекция dl на вектор   ,  но   , где R – расстояние от прямой тока I до dl.

 .

      Отсюда

,

      это теорема о циркуляции вектора   :  циркуляция вектора магнитной индукции равна току, охваченному контуром, умноженному на магнитную постоянную.

2. Рівняння зміщення та амплітуди механічних загасаючих коливань. Добротність коливної системи

Білет №14

Рух заряджених частинок в електричному та магнітному полях (електрична та магнітна сила, траєкторія)

рух заряджених частинок у електричному полі.

Якщо електричний заряд розміщений у електричному полі, то на нього діє сила: ( 13 )

Якщо заряд вільний та може рухатися, то за другим законом Ньютона: 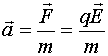(14 )

Якщо електричне поле стале і прискорення руху частинки теж стале, то формули кінематики опишуть рух частинки. Положення заряда у будь- який момент часу можна визначити за формулою:

(15 )

швидкість частинки буде рівна: .

рух заряджених частинок у магнітному полі.

Більш загальним є випадок руху частинок, які влітають у магнітне поле під гострим кутом  Розкладемо вектор швидкості частинки на дві складові: нормальну і тангенціальну і розглянемо два прості рухи частинки.

1. Зі швидкістю частинка рухається дугою кола у площині, перпендикулярній до напрямку поля, причому:

.

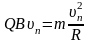Радіус кола

період обертання частки в магнітному полі

.

2. Зі швидкістю частинка рухається вздовж напрямку магнітного поля. У результаті накладання двох рухів частинка рухається вздовж гвинтової лінії. Крок гвинтової лінії:

.

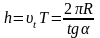2. Скласти диференціальне рівняння електромагнітних загасаючих коливань та знайти його розв’язок.

Рівняння коливань, тобто рівняння, що описує залежність зміщення х від часу t, можна, знайти використовуючи закони механіки. За другим законом динаміки швидкість зміни імпульсу дорівнює сумі всіх сил, які діють на тіло:

Надалі знаки векторів можна не записувати, оскільки рух одновимірний. Тіло вважатимемо матеріальною точкою з масою m. У нашому випадку діє єдина сила — пружна повертаюча сила F_пр. Згідно із законами Гука при малих зміщеннях сила пружності прямо пропорційна до зміщення: F_пр = -kx

Знак «мінус» означає, що сила направлена в бік, протилежний зміщенню. Коефіцієнт пропорційності k називається коефіцієнтом жорсткості пружного елемента. Маса m стала, і тому

або

Поділивши обидві частини рівняння на масу m і позначивши

дістанемо диференціальне рівняння вільних незгасаючих коливань

.

Загальний розв'язок цього лінійного диференційного рівняння другого порядку відомий:

x = A cos (ω₀t + φ₀)

Білет №15

Ефект Холла в провідниках та напівпровідниках. Залежність холівської напруги від концентрації зарядів.

Ефект Холла

      Коли провідник із струмом, що протікає по ньому, поміщається в магнітне поле так, що напрям струму виявляється перпендикулярним магнітним силовим лініям, то утворюється поперечне електричне поле, пропорційне добутку щільності магнітного потоку і силі електричного струму. Цей ефект виникає в провідниках, проте найбільш суттєвий він в напівпровідниках, де відомий під назвою ефекту Холла.

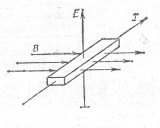
На мал. показана напівпровідникова пластина, до якої прикладено магнітне поле з індукцією В, перпендикулярне струму I, що протікає через неї, і електричне поле, що виникає при цьому, з напруженістю Е. Відношення між магнітною індукцією, струмом і напруженістю визначається таким чином: E = - RH (IB)

де   RH  = 1/ne     - коефіцієнт Холла; п - концентрація зарядів, що протікають через одиницю об'єму і утворюють електричний струм в провіднику або напівпровіднику; е - заряд носія зарядів.

      Ефект Холла використовується в багатьох типах перетворювачів, призначених для виміру магнітного поля, а також в безконтактних перемикальних приладах.

Залежність

Основний внесок у залежність 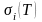вносить концентрація носіїв заряду (13), яка залежить від температури як

.

У той же час для невиродженого напівпровідника у високотемпературному наближенні , тому що , а 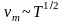. Таким чином,

, (14)

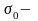константа, яка не залежить від температури.

На дослідженні залежності питомої електричної провідності (чи опору) власного напівпровідника від температури (14) заснований один з методів визначення ширини забороненої зони.

№2 Залежність енергії вільних коливань від часу та добротності коливної системи

16 білет
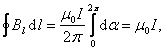