4.4. Прямоугольная симметричная потенциальная яма

Прямоугольная потенциальная яма есть потенциальный барьер, вывернутый наизнанку. Потенциал (рис. 4.10) описывается функцией

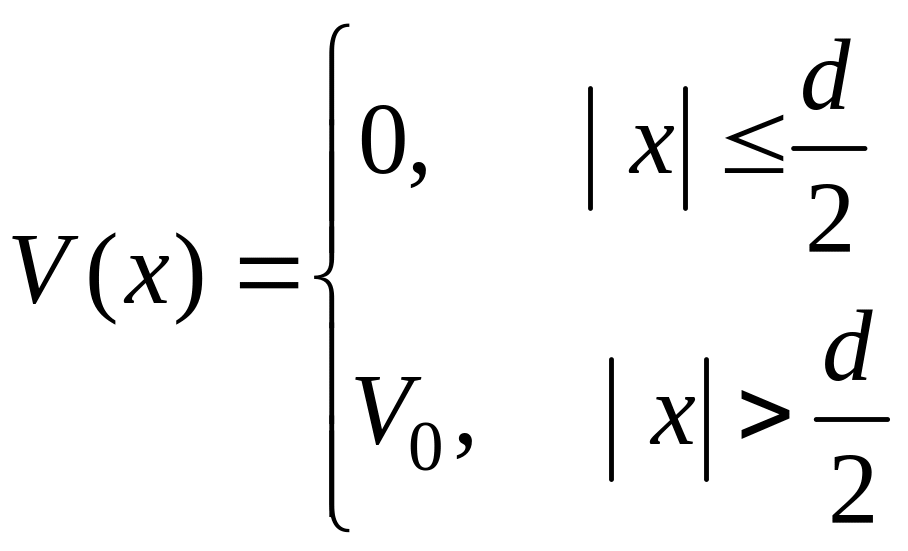
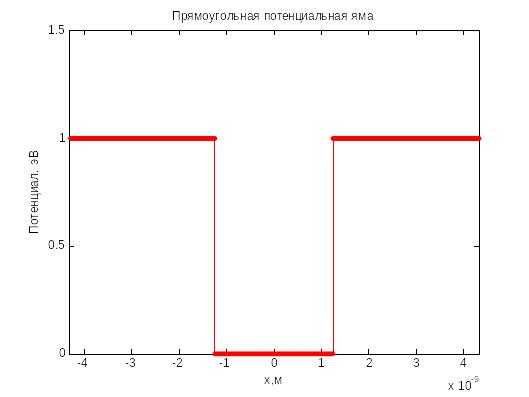
Рис. 4.10.

Рассмотрим электрон с энергией . Его движение неограниченно. В трёх областях постоянного потенциала уравнения Шрёдингера имеют вид

Или в стандартном виде ОДУ

Решения их

(4.21)

На границах должны выполняться условия непрерывности

После подстановки в них волновых функций (4.13) получим четыре уравнения для коэффициентов :

Умножим первое уравнение на и сложим его со вторым:

Третье уравнение умножим на и вычтем его из четвёртого:

Вместо и будем искать новые неизвестные переменные

Для них имеем систему уравнений

+

из которой находим

(4.24)

Коэффициенты и равны

(4.25)

(4.26)

Формулы (4.22), (4.24) – (4.26) полностью определяют волновую функцию электрона, движущегося над потенциальной ямой. На волновые числа , а, значит, и на энергию электрона, не накладывается каких-либо ограничений – она может принимать непрерывный ряд значений от до . Аналогично предыдущему параграфу запишем коэффициенты отражения электрона от ямы и его прохождения над ямой,

(4.27)

(4.28)

Зависимость коэффициента отражения от ямы и прохождения над ямой от энергии при показана на рис. 4.11.

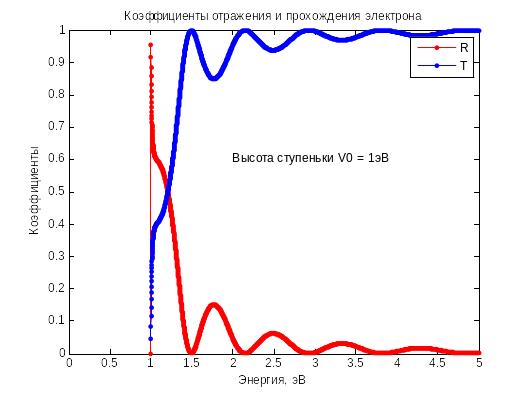
Рис. 4.11

Здесь, как и в случае надбарьерного прохождения, наблюдается немонотонное, колебательное поведение коэффициентов отражения и прохождения. Это следствие интерференции падающей и отражённой электронной волн. При некоторых энергиях коэффициент прохождения точно равен единице, но при промежуточных энергиях он меньше единицы, и у электрона имеется заметная вероятность отразиться от потенциальной ямы.

Пусть теперь энергия электрона . В этом случае в трёх областях имеем уравнения

Решения и в областях и вещественны:

(4.29)

Чтобы они оставались конечными и при , следует положить . На границах ямы волновые функции удовлетворяют условиям непрерывности (4.14):

Умножим первое уравнение на и вычтем из него второе уравнение, а затем третье уравнение умножим на и сложим его с четвёртым:

В отличие от (4.15) получили однородную систему уравнений для коэффициентов . Перепишем её для переменных

, .

Она имеет нетривиальное решение, только если её детерминант равен нулю,

Раскрывая его, получим нелинейное дисперсионное уравнение для определения разрешённых собственных значений энергии электрона в потенциальной яме

Перегруппировав слагаемые, его можно записать в виде

или

Для симметричной ямы получаем

От энергии зависят и . С целью упрощения определим новую переменную . Тогда и дисперсионное уравнение принимает вид

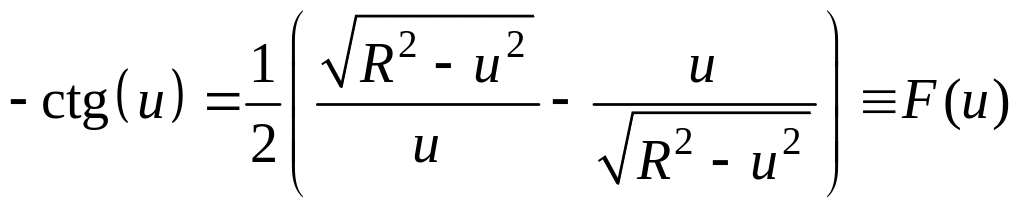(4.31)

Решить его можно только численно. Графическое решение представлено на рис. 4.11. Он позволяет сделать важные выводы.

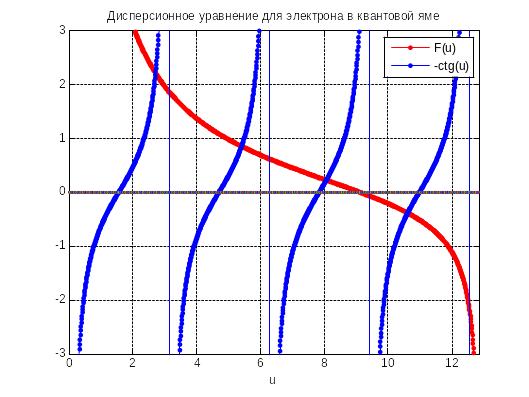
Рис. 4.11.

1. Спектр энергий электрона, локализованного в потенциальной яме, дискретный.

2. В яме конечной глубины существует конечное число разрешённых уровней энергии

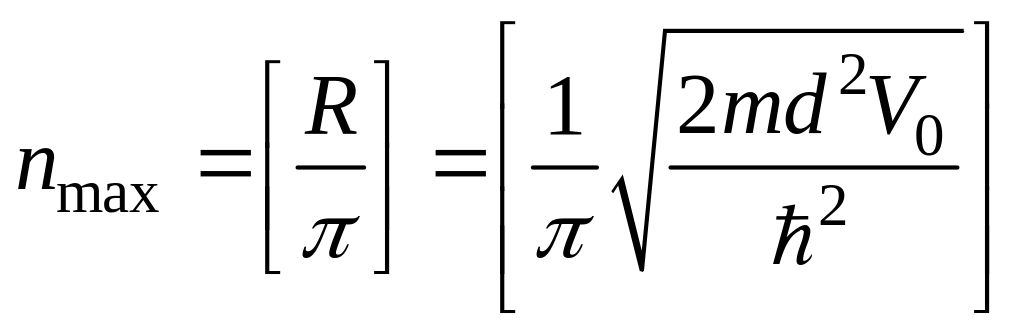
3. В яме сколь угодно малой глубины существует связанное состояние электрона с энергией

,

4. Второй уровень появляется при или .

Волновые функции связанного и несвязанного состояний электрона показаны на рис.4.12.

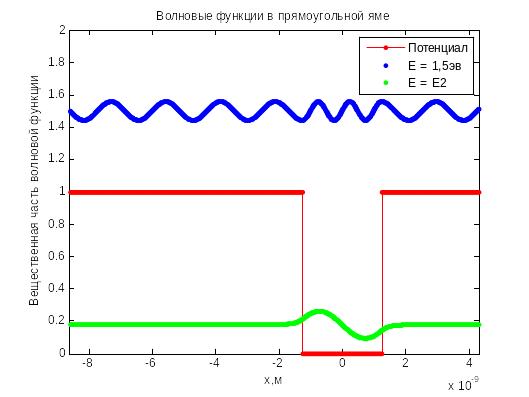
Рис. 4.12

Волновая функция основного связанного состояния , соответствующего нижайшей энергии , в симметричной яме всегда чётная, то есть симметричная относительно центра ямы. Волновая функция состояния с энергией нечётная, именно она изображена на рис 4.12.

В общем случае .