4.3. Прямоугольный потенциальный барьер

Рассмотрим общий случай несимметричного потенциального барьера (рис. 4.5).

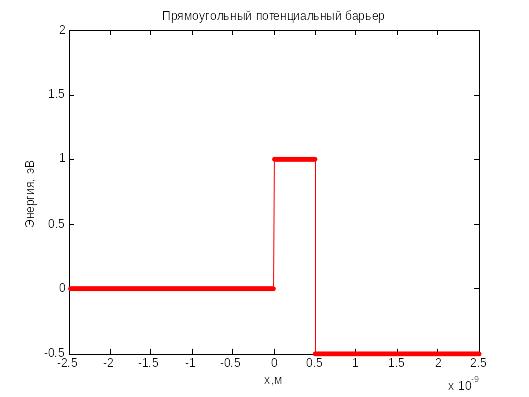
Рис. 4.5

Формальная схема нахождения волновых функций и энергетического спектра не отличается от случая потенциальной ямы. Именно, для трёх областей записываем уравнение Шрёдингера,

Или в стандартном виде ОДУ

Решения их

(4.13)

подчинены условиям непрерывности на границах и ,

После подстановки (4.13) в (4.14) получим систему уравнений для коэффициентов , из которой находим

Через коэффициенты и выражаем плотности потоков вероятности

и находим коэффициенты отражения и прохождения,

(4.16)

(4.17)

Волновые функции и для значений энергии электрона и показаны на рис. 4.6 для барьера толщиной и на рис. 4.7 для барьера толщиной . На рис. 4.8 и 4.9 показаны коэффициенты прохождения и отражения для тех же барьеров.

Волновая функция справа от барьера толщиной имеет осциллирующий характер, даже если энергия электрона меньше высоты барьера. Это значит, что электрон преодолевает барьер и проникает в область без потери энергии и продолжает движение в положительном направлении. Это явление называется квантовым туннелированием или туннельным эффектом. Оно обусловлено волновыми свойствами частиц и наблюдается только при очень малых их массах и тонких барьерах. Коэффициент есть вероятность туннелирования.

При толщине барьера волновая функция в области практически экспоненциально стремится к нулю. Вместе с ней стремится к нулю и вероятность туннелирования.

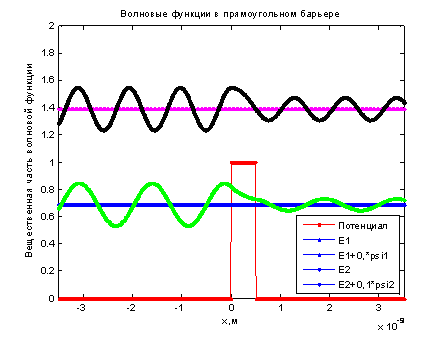
Рис. 4.6

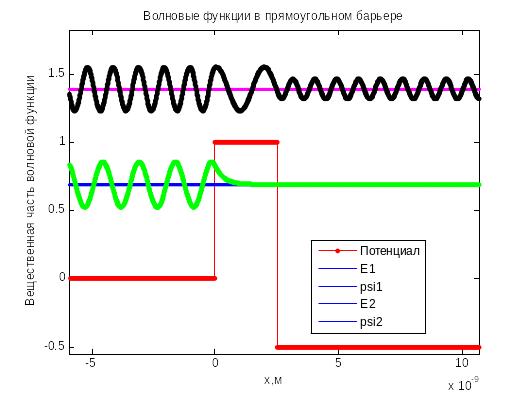
Рис. 4.7

При энергии электрона, большей высоты барьера , как и в случае ступенчатого потенциала, электрон не обязательно всегда окажется справа от барьера. Имеется конечная вероятность его отражения. Но появляется и качественное отличие от ступенчатого потенциала. Вероятности отражения и прохождения как функции энергии имеют осциллирующий характер. Причём амплитуда и частота осцилляций возрастают с ростом толщины барьера. Имеются энергии, при которых электрон пролетит над барьером со стопроцентной вероятностью. Эти энергии называются резонансными. Но при промежуточных энергиях имеется заметная вероятность отражения. Осциллирующий характер зависимостей и обусловлен интерференцией электронных волн, отражённых от фронтальной и тыльной границ барьера.

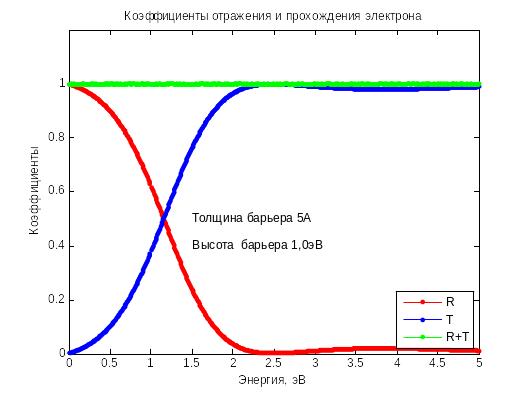
Рис. 4.8

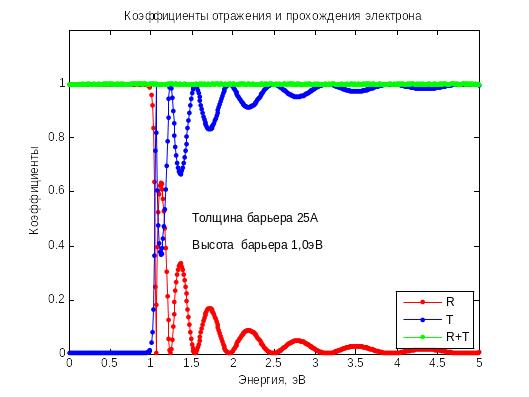
Рис. 4.9

Формула (4.17) даёт точное выражение коэффициента прохождения , пригодное для любых энергий и любого профиля барьера. Для симметричного барьера при формулу (4.17) можно упростить до гораздо более наглядного вида. В этом случае

Если энергия далека от вершины барьера, так что , то , поэтому . При этих условиях из (4.28) после сокращения на получаем

(4.18)

Особенно просто выглядит коэффициент прохождения при ,

(4.19)

Он экспоненциально зависит от толщины барьера и субэкспоненциально от его высоты . С помощью (4.19) можно оценить толщину барьера, при которой вероятность туннелирования принимает заданную величину. Например, для барьера высотой и толщиной

При для симметричного барьера получаем

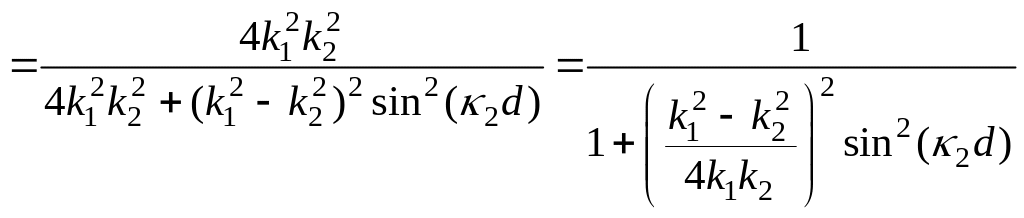
Коэффициент прохождения максимален, когда или

Подставив , найдём резонансные значения энергии электрона,

(4.20)