Глава 4. Движение электрона в одномерных ступенчатых потенциалах
4.1. Свободный электрон
Свободный электрон
движется в пустом пространстве, где его
потенциальная энергия
,
в направлении оси
.
Уравнение Шрёдингера имеет вид
(4.1)
Запишем его в стандартном виде обыкновенного дифференциального уравнения с постоянными коэффициентами,
(4.2)
(4.3)
Общее решение его
есть суперпозиция двух плоских волн:
,
распространяющейся в
положительном направлении, и
,
распространяющейся в отрицательном
направлении,
(4.4)
Постоянные
и
определяются граничными условиями при
,
задающими плотность потока электронов.
Из (4.3) находим энергию электрона в
состоянии
,
Собственное
значение
может быть любым положительным числом,
поэтому и энергия может принимать любые
значения. Свободный
электрон обладает непрерывным
энергетическим спектром.
Зависимость
называется законом
дисперсии
частицы. Для свободного электрона он
определяется единственным параметром
– массой частицы
(рис.
4.1).
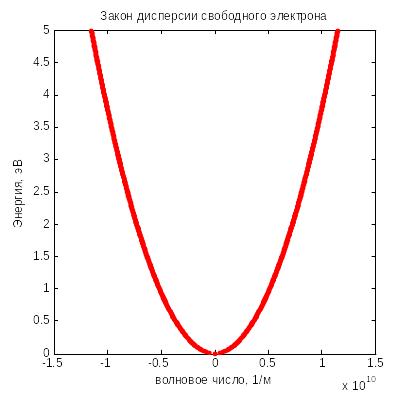
Рис. 4.1 Параболический закон дисперсии свободного электрона
4.2. Потенциальная «ступенька»
Потенциал имеет вид (рис. 4.2)
На всей действительной оси справедливо уравнение Шрёдингера
(4.5)
В областях постоянства потенциала оно принимает вид
при
при
(4.6)
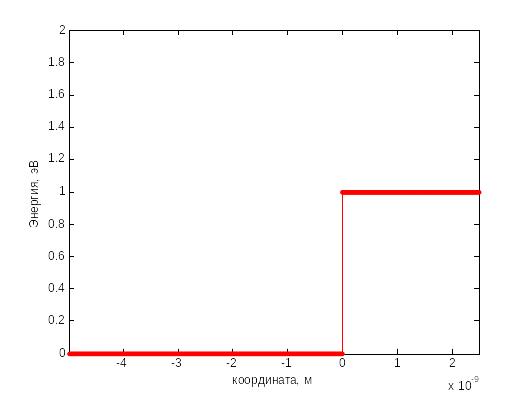
Рис. 4.2. Ступенчатый потенциал
На всей действительной оси справедливо уравнение Шрёдингера
(4.5)
В областях постоянства потенциала оно принимает вид
при при
(4.6)
Энергия
одна и та же в обеих областях, волновые
же функции отличаются.. Полная волновая
функция есть
На границе должны выполняться условия непрерывности
(4.7)
Пусть
.
Уравнения (4.6) запишем в однородном виде
Общие решения их имеют вид
Постоянные должны
определяться из граничных условий при
и
.
Будем считать, что электрон движется
из
в положительном направлении оси
.
Тогда следует положить
.
При
имеется только электрон, движущийся в
положительном направлении, поэтому
полагаем
.
Для
и
из условий (4.7) после подстановки в них
волновых функций
(4.8)
получаем систему линейных уравнений
(4.9)
Решая её, находим
, 
(4.10)
Таким образом,
Найдём плотности
потоков вероятностей в состояниях
,
и
.
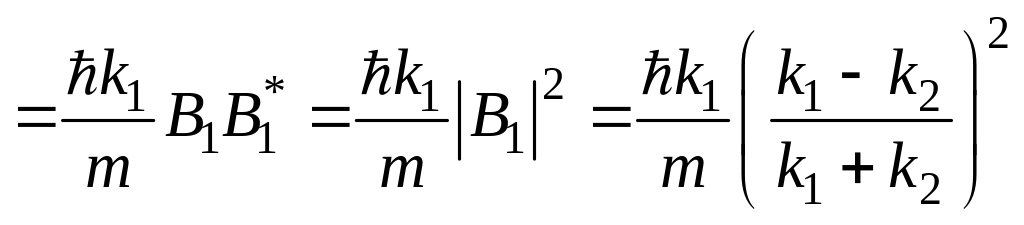
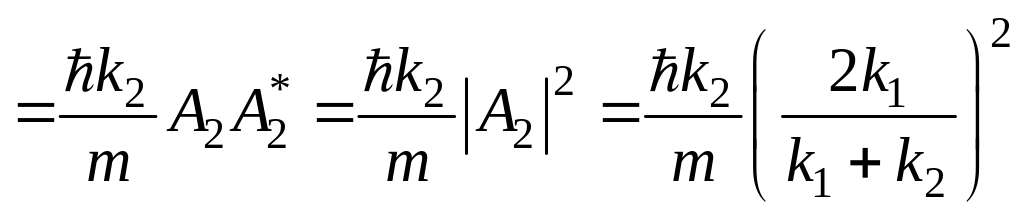
Найдём сумму
потоков
и
:
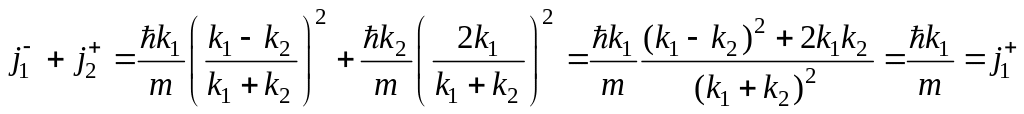Таким
образом, плотность потока вероятности
сохраняется - падающий поток равен сумме
отражённого и прошедшего потоков.
Распределение потоков можно определить
коэффициентом отражения
и коэффициентом прохождения
,
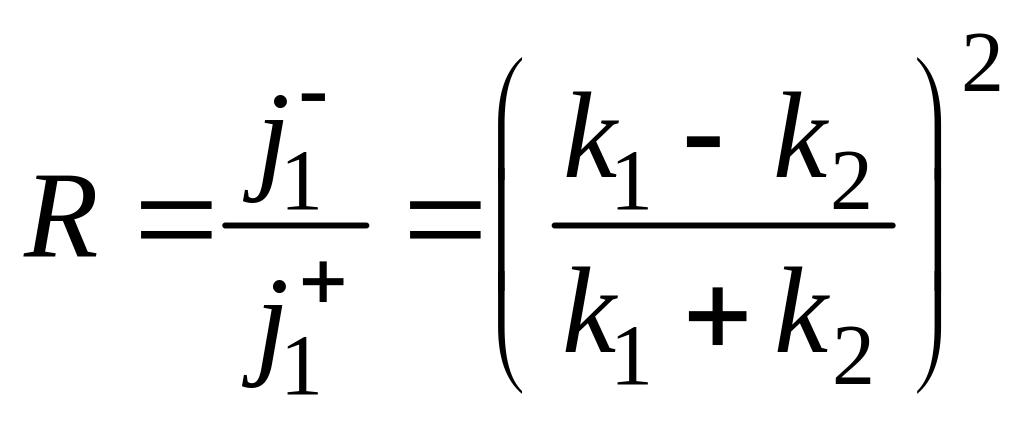(4.11)
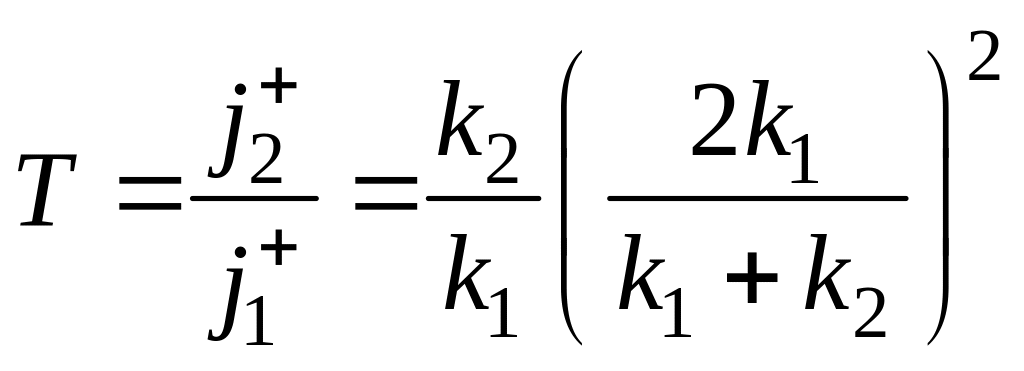(4.12)
Коэффициенты отражения и преломления зависят от энергии электрона. Эта зависимость показана на рис. 4.3.
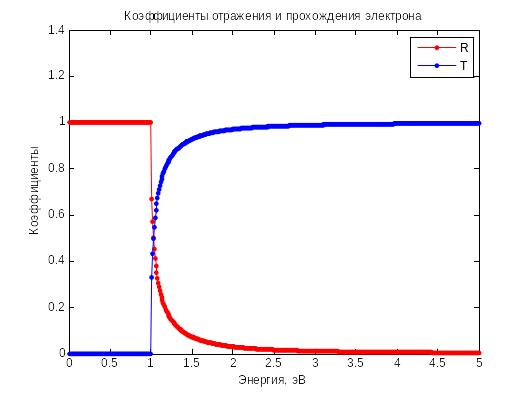
Рис. 4.3.
Волновая функция
электрона в ступенчатом потенциале
есть синусоида (рис. 4.4, синий цвет), длина
волны которой скачком меняется на
границе. Поскольку
,
то
.
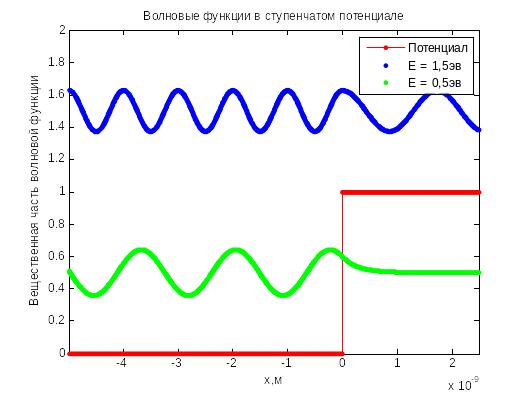
Рис. 4.4.
Пусть теперь
.
Уравнения Шрёдингера для
и
имеют вид
Общие решения их
Как и в первом
случае, в
полагаем
.
Функция должна быть везде, в том числе
и при
,
конечной. Поэтому следует положить
.
Волновая функция
в области не является распространяющейся
волной, а экспоненциально затухает. На
расстоянии
она уменьшается в
раз и имеет заметную величину до глубины
.
Из граничных условий при получаем уравнения
и находим
, 
Вычислим потоки
вероятности в состояниях
,
и
.
Таким образом, в состояниях с энергией электрон полностью отражается от барьера,
,
Волновая функция состояния с энергией показана на рис. 4.4 зелёным цветом.