6Б Задача о распределении ресурсов (вариант б)

Распределение мест в самолете

Неформальное описание задачи

Пусть авиакомпания продает билеты на плановый рейс самолета. Продажа билетов начинается задолго до запланированной даты вылета. При заблаговременной покупке билетов пассажиры получают на билеты скидку. Непосредственно перед вылетом билеты продаются по полной стоимости. Все непроданные заблаговременно со скидкой билеты поступают в продажу по полной стоимости. Предполагается, что никто из пассажиров купленные на рейс билеты не сдает. Доход авиакомпании определяется стоимостью проданных билетов. В случае, если авиакомпания оставляет на продажу по полной стоимости меньше билетов, чем наблюдается спрос, то авиакомпания не получает части дохода, который определяется разницей между стоимостью билетов по полной цене и билетами со скидкой и спросом на билеты по полной цене. В случае, если авиакомпания принимает решение продавать больше билетов по полной цене, чем на них наблюдается спрос, то компания теряет доход равный стоимости непроданных билетов. Задача сводится к выбору оптимального соотношения между количеством билетов, продаваемых по полной цене и количеством билетов, продаваемых со скидкой.

Формальная постановка задачи.

Множество решений , где - решение продавать билетов со скидкой, M – общее количество мест в самолете. Тогда под по полной стоимости продается ( ) билетов. Стоимость билетов со скидкой равна , стоимость билетов без скидки составляет . Покупательский спрос на билеты со скидкой описывается непрерывной случайной величиной X, принимающей значения из множества , где - спрос на билетов со скидкой. Случайная величина X описывается плотностью распределения на интервале . Покупательский спрос на билеты по полной стоимости описывается непрерывной случайной величиной Y, принимающей значения из множества , где - спрос на билетов по полной стоимости. Случайная величина Y описывается плотностью распределения на интервале . , - представляют собой независимые случайные величины.

Расчет полезностей решений

Полезность некоторого решения с учетом результатов, полученных в задаче 5а равна:

,

где ,

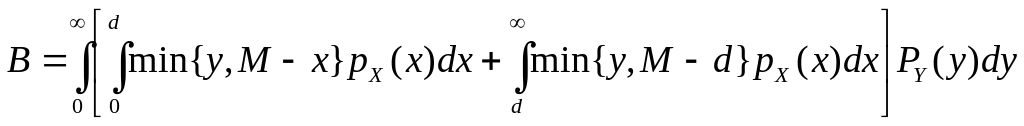
Выполнив дальнейшие преобразования В можно получить аналитическое решение задачи, однако это сложно и проще воспользоваться маржинальным анализом в возможностях которого мы убедились при анализе newboys problem.

Маржинальный анализ

Маржинальный анализ предполагает сравнение доходности решений и . В качестве базы для сравнения используется решение . На рисунке показано дерево решений.

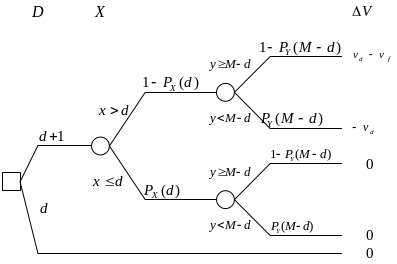
Изменение доходности от решения по отношению к полезности решения равно:

Приравнивая к нулю, получаем оптимальное с точки зрения байесовского подхода решение : .

Тогда , откуда

Получается, что наилучшее в байесовском смысле решение полностью определяется соотношением . Графическое решение показано на рисунке ниже.

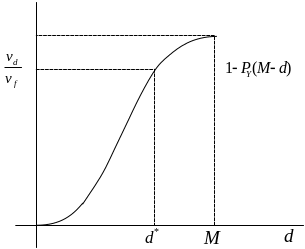
Вычислим минимум цены , ниже которого нет смысла опускаться. Если , то , т. е. все билеты следует продавать без скидки.

Динамическое принятие решений

Динамическое принятие решений предполагает принятие решений в зависимости от текущего состояния окружающей среды, в связи с чем решение в различные моменты времени может отличаться. На рисунке показано дерево решений.

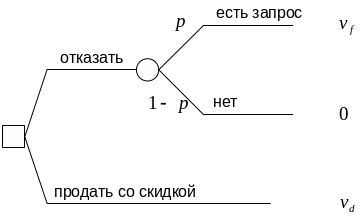
При поступлении запроса на билет со скидкой в случае, если > принимается решение не продавать билеты со скидкой, иначе билет продается со скидкой.